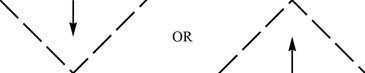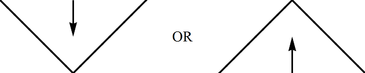Difference between revisions of "Conformal diagrams: stationary black holes"
| (10 intermediate revisions by the same user not shown) | |||
| Line 157: | Line 157: | ||
<p style="text-align: left;">Starting from any one of the four pieces, there is only one way to assemble the diagram, and one has to use all the parts: | <p style="text-align: left;">Starting from any one of the four pieces, there is only one way to assemble the diagram, and one has to use all the parts: | ||
| − | <gallery widths=300px heights=300px perrow=2 caption="The puzzle pieces: two for the exterior region (above) and two for the interior region (below). | + | {|class="wikitable" style="margin: 1em auto 1em auto;" |
| − | + | |<gallery widths=300px heights=300px perrow=2 caption="The puzzle pieces: two for the exterior region (above) and two for the interior region (below)."> | |
File:Conf-BH-SchwExtA.png | File:Conf-BH-SchwExtA.png | ||
File:Conf-BH-SchwExtB.png | File:Conf-BH-SchwExtB.png | ||
| Line 164: | Line 164: | ||
File:Conf-BH-SchwIntB.png | File:Conf-BH-SchwIntB.png | ||
</gallery> | </gallery> | ||
| + | |} | ||
| − | The horizon structure is very similar to that of full de Sitter spacetime in open slicing or | + | The horizon structure is very similar to that of full de Sitter spacetime in open slicing or "static" coordinates (the notions and properties of R- and T-regions apply equally well), while the structure of infinity is the same as that of Minkowski, and additionally there are singularities. |
Finally, one could note that the form of the conformal block for the exterior solution was determined from the start. First, we have asymptotic flatness, therefore the Minkowski's structure of infinity. This is already half of the block's boundary. | Finally, one could note that the form of the conformal block for the exterior solution was determined from the start. First, we have asymptotic flatness, therefore the Minkowski's structure of infinity. This is already half of the block's boundary. | ||
{|class="wikitable" style="margin: 1em auto 1em auto;" | {|class="wikitable" style="margin: 1em auto 1em auto;" | ||
| − | |[[File:Conf-BH-SchwFull.png|center|thumb|365px| | + | |[[File:Conf-BH-SchwFull.png|center|thumb|365px|The full conformal diagram for the (maximally extended) Schwarzschild solution.]] |
| − | + | ||
|} | |} | ||
</p> | </p> | ||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Other spherically symmetric black holes == | |
| − | + | ||
| − | + | The Schwarzschild metric (\ref{SchwBH}) is the vacuum spherical symmetric solution of Einstein's equation. If we add some matter, we will obtain a different solution, e.g. Reissner-Nordstr\"{o}m for an electrically charged black hole. In all cases, spherical symmetry means that in appropriately chosen coordinate frame the metric takes the same form (\ref{SchwBH}), | |
| − | + | \begin{equation} | |
| − | + | ds^2 =f(\rho)dt^2 -\frac{d\rho^2}{f(\rho)}-r^2 (\rho)d\Omega^2 , | |
| − | + | \end{equation} | |
| − | + | but with some different function $f(\rho)$: one can always ensure that the metric functions have this form by choosing the appropriate radial coordinate\footnote{It is sometimes called the ``quasiglobal coordinate''} $\rho$. The angular part $\sim d\Omega^2$ does not affect causal structure and conformal diagrams. The zeros $\rho=\rho^\star$ of $f(\rho)$ define the surfaces, which split the full spacetime into R- and T-regions and are the horizon candidates. | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<div id=""></div> | <div id=""></div> | ||
| − | === Problem | + | === Problem 5: Killing horizons. === |
| − | + | Consider radial geodesic motion of a massive or massless particle. Make use of the integral of motion $E=-u^\mu \xi_\mu$ due to the Killing vector and find $\rho (t)$ and $\rho(\lambda)$, where $\lambda$ is the affine parameter (proper time $\tau$ for massive particles)<br/> | |
| + | '''(a)''' When is the proper time of reaching the horizon $\tau^\star =\tau (\rho^\star)$ finite? | ||
| + | '''(b)''' Verify that surface $\rho=\rho^\star$ is a Killing horizon | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">The formulas derived for Schwarzschild (\ref{BH-energy}) and (\ref{BH-lambda}) still work, just now $f(\rho)$ is not fixed. |
| + | <br/> | ||
| + | '''(a)'''As for almost all particles $d\tau /d\rho$ stays bounded, the proper time of reaching the horizon candidate at $\rho=\rho^\star$ is finite if and only if $\rho^\star$ itself is finite. Otherwise we would have the "horizon" at infinite proper distance. It can be called a remote horizon, but extension across such a surface is not possible and not needed, as spacetime in that direction is already geodesically complete.<br/> | ||
| + | '''(b)''' The Killing vector that forms the horizon is $\xi_t =\partial_t$, its norm $|\xi_t |^2 =g_{tt}=f$. Thus $\rho=\rho^\star$ is indeed a Killing horizon by definition.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
<div id=""></div> | <div id=""></div> | ||
| − | |||
| − | + | === Problem 6: Extension across horizons. === | |
| − | + | Let us shift the $\rho$ coordinate so that $\rho^\star =0$, and assume that | |
| − | + | \begin{equation} | |
| − | + | f(\rho)=\rho^{q}F(\rho),\qquad q\in\mathbb{N}, | |
| − | + | \end{equation} | |
| − | + | where $F$ is some analytic function, with $F(0)\neq 0$. Suppose we want to introduce a new radial "tortoise" coordinate $x$, such that the two-dimensional part of the metric in terms of $(t,x)$ has the conformally flat form: | |
| − | + | \begin{equation} | |
| − | + | ds^2_2 =f(\rho(x))\big[dt^2 -dx^2 \big]. | |
| − | = | + | \end{equation} |
| + | '''(a)'''What is the asymptotic form of relation $\rho (x)$?<br/> | ||
| + | '''(b)''' Rewrite the metric in terms of null coordinates | ||
| + | \begin{equation} | ||
| + | V=t+x,\qquad W=t-x. | ||
| + | \end{equation} | ||
| + | Where is the horizon in terms of these coordinates? Is there only one?<br/> | ||
| + | '''(c)''' Suppose we pass to new null coordinates $V=V(v)$ and $W=W(w)$. What conditions must be imposed on functions $V(v)$ and $W(w)$ in order for the mixed map $(v,W)$ to cover the past horizon and the map $(w,V)$ to cover the future horizon without singularities? | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"> | + | <p style="text-align: left;">'''(a)''' Integrating $dx=f^{-1}d\rho$, one obtains |
| − | </ | + | \begin{equation} |
| − | </ | + | \rho\sim \left\{\begin{array}{l} |
| + | e^{xF(0)},\quad \text{for}\quad q=1,\\ | ||
| + | |x|^{-1/(q-1)}\quad\text{for}\quad q>1 . | ||
| + | \end{array}\right. | ||
| + | \end{equation} | ||
| + | We see that $x\to -\infty$ at the horizon. It converges for $q<1$, but in this case one can show that the Kretschmann scalar $R_{\mu\nu\rho\sigma}R^{\mu\nu\rho\sigma}$ diverges, so this is not a horizon but a singularity. | ||
| + | <br/> | ||
| + | '''(b)''' $ds^2 =f \; dV\;dW$; the horizon is at $x\to -\infty$ while $t$ is fixed, so in terms of $V$ and $W$ it is split into two parts: the future horizon at $V\to -\infty$ while $W$ is fixed, and the past horizon at $W\to +\infty$ while $V$ is fixed. | ||
| + | <br/> | ||
| + | '''(c)''' Near the past horizon in terms of $(v,W)$ the metric takes form | ||
| + | \begin{equation} | ||
| + | ds^2 =\Big(f \frac{dW}{dw}\Big)\; dV\; dw, | ||
| + | \end{equation} | ||
| + | while $W\approx -x$, so for it to be regular there we need | ||
| + | \begin{equation} | ||
| + | \frac{dW}{dw}\sim f^{-1}\sim \rho^{q} \sim \left\{ | ||
| + | \begin{array}{l} | ||
| + | |x|^{(1-q)/q}\sim W ^{(1-q)/q}\quad\text{for}\quad q>1 ,\\ | ||
| + | e^{xF(0)}\sim e^{-WF(0)}\quad\text{for}\quad q= 1, | ||
| + | \end{array}\right. | ||
| + | \end{equation} | ||
| + | and after integrating | ||
| + | \begin{equation} | ||
| + | W\sim \left\{\begin{array}{l} | ||
| + | w^{1-q}\quad\text{for}\quad q>1 ,\\ | ||
| + | \ln w\quad\text{for}\quad q= 1. | ||
| + | \end{array}\right. | ||
| + | \end{equation} | ||
| + | The same way the asymptotic relation $V(v)$ is found near the future horizon. | ||
| − | + | Thus a horizon candidate $\rho=\rho^\star$ is defined by condition $f(\rho^\star)=0$. If $\rho^\star =\pm\infty$, then the proper time of reaching it diverges, so it is not a horizon, but an infinitely remote boundary of spacetime. It can be a remote horizon if $x^\star =\pm \infty$. In case $x^\star =O(1)$ the candidate is not a horizon, but a singularity, so again there is no continuation. An asymptotically flat spacetime by definition has the same structure of infinity as that of Minkowski spacetime; in general this is not always the case---recall the de Sitter and other cosmological spacetimes.</p> | |
| − | === | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</div> | </div> | ||
</div> | </div> | ||
<div id=""></div> | <div id=""></div> | ||
| − | |||
| − | + | === Problem 7: Infinities, horizons, singularities. === | |
| − | + | Draw the parts of conformal diagrams near the boundary that correspond to the limiting process | |
| − | + | \begin{equation} | |
| − | + | \rho\to\rho_0 ,\qquad |\rho_0|<\infty, | |
| − | </ | + | \end{equation} |
| − | </ | + | under the following conditions: |
| − | + | <br/> | |
| − | + | '''(a)''' spacelike singularity: $f(\rho_0)>0$, $|x_0 |<\infty$;<br/> | |
| − | = | + | '''(b)''' timelike singularity: $f(\rho_0)<0$, $|x_0 |<\infty$;<br/> |
| + | '''(c)''' asymptotically flat infinity: $\rho_0 =\pm \infty$, $f(\rho)\to f_0>0$;<br/> | ||
| + | '''(d)''' a horizon in the R region: $f(\rho)\to +0$, $|x_0 |\to \infty$;<br/> | ||
| + | '''(e)''' a horizon in the T region: $f(\rho)\to -0$, $|x_0 |\to \infty$;<br/> | ||
| + | '''(f)''' remote horizon in a T-region: $\rho_0 =\pm \infty$, $f(\rho)\to -<0$;<br/> | ||
| + | Remember that any spacelike line can be made "horizontal" and any timelike one can be made "vertical" by appropriate choice of coordinates. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"> | + | <p style="text-align: left;">'''(a)''' Horizontal line, approached either from above or from below; it acts as the boundary of spacetime -- there is no continuation across (see Fig.); |
| − | + | ||
| − | + | ||
| − | + | {|class="wikitable" style="margin: 1em auto 1em auto;" | |
| − | + | |[[File:Conf-BH-SingSpace.png|center|thumb|365px|Space-like singularity.]] | |
| + | |} | ||
| − | + | '''(b)''' Vertical line, approached either from the left or from the right; as it is singular, there is again no continuation (see Fig.); | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | {|class="wikitable" style="margin: 1em auto 1em auto;" | |
| − | + | |[[File:Conf-BH-SingTime.png|center|thumb|365px|Time-like singularity.]] | |
| + | |} | ||
| − | + | '''(c)''' This is the infinitely remote part of Minkowski spacetime, from future infinity, to future null infinity, to spacelike infinity, to past null infinity, and finally to past infinity; it can constitute either the left or the right boundary of a conformal block and has the shape of "$>$" or "$<$" (see Fig. \ref{Conf-BH-InfMink}); | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | {|class="wikitable" style="margin: 1em auto 1em auto;" | |
| − | + | |[[File:Conf-BH-InfMink.png|center|thumb|365px|Minkowski infinity.]] | |
| + | |} | ||
| − | + | '''(d)''' The same as the Schwarzschild horizon as approached from the exterior region: the two sides of a triangle pointed left "$<$" or right "$<$" and approached from the inside; thus the shape is the same as above, but now the horizon allows continuation across (see Fig.); | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | {|class="wikitable" style="margin: 1em auto 1em auto;" | |
| − | + | |[[File:Conf-BH-HorExt.png|center|thumb|365px|Horizon as boundary of an R-region.]] | |
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(e)''' The same as Schwarzschild horizon as approached from the interior region: two sides of a triangle pointed up "$\wedge$" or down "$\vee$" and approached from the inside (see Fig.). | |
| − | + | ||
| − | + | {|class="wikitable" style="margin: 1em auto 1em auto;" | |
| − | + | |[[File:Conf-BH-HorInt.png|center|thumb|365px|Horizon as boundary of a T-region]] | |
| − | + | |} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | '''(f)''' Two diagonal lines -- a corner of a triangle, -- pointed up or down, and approached from the inside. Thus the shape is the same as in the previous case, "$\wedge$" or "$\vee$"; the difference is that now there is no continuation across (see Fig.). | |
| − | + | ||
| − | + | {|class="wikitable" style="margin: 1em auto 1em auto;" | |
| − | + | |[[File:Conf-BH-InfTime.png|center|thumb|365px|Remote horizon as a boundary of a T-region]] | |
| − | + | |} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | < | + | <br/> |
| − | + | For arbitrary $f(\rho)$ we can | |
| − | + | <br/> | |
| − | < | + | 1) split the full spacetime into regions between the zeros $\rho_i$ of $f(\rho)$;<br/> |
| − | + | 2) draw for each region the conformal diagram, which is a square $\Diamond$ or half of it $\triangle$, $\nabla$, $\triangleleft$, $\triangleright$;<br/> | |
| − | + | 3) glue the pieces together along the horizons $\rho=\rho_i$, while leaving singularities and infinities as the boundary. | |
| − | + | <br/> | |
| + | The resulting diagram can turn out to be either finite, as for Schwarzshild, when singularities and infinities form a closed curve enclosing the whole spacetime, or not.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
<div id=""></div> | <div id=""></div> | ||
| − | === Problem | + | === Problem 8: Examples. === |
| + | Draw the conformal diagrams for the following spacetimes: | ||
| − | + | 1) Reissner-Nordstrom charged black hole: | |
| − | + | \begin{equation} | |
| − | + | f(r)=1-\frac{r_g}{r}+\frac{q^2}{r^2}, \qquad 0<q<r_{g},\qquad r>0; | |
| − | + | \end{equation} | |
| − | < | + | |
| − | + | ||
| − | + | 2) Extremal Reissner-Nordstr\"{o}m charged black hole | |
| − | + | \begin{equation} | |
| + | f(r)=\Big(1-\frac{q}{r}\Big)^2, \qquad q>0,\qquad r>0; | ||
| + | \end{equation} | ||
| + | 3) Reissner-Nordstrom-de Sitter charged black hole with cosmological constant (it is not asymptotically flat, as $f(\infty)\neq 1$) | ||
| + | \begin{equation} | ||
| + | f(r)=1-\frac{r_g}{r}+\frac{q^2}{r^2}-\frac{\Lambda r^2}{3}\qquad q,\Lambda>0; | ||
| + | \end{equation} | ||
| + | analyze the special cases of degenerate roots. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"> | + | <p style="text-align: left;">1) In the generic case there are two positive roots $+\infty>r_+ >r_- >0$, which give horizons, while $r=0$ is a singularity. This gives us three regions between the roots: (a) $r\in(r_+ ,+\infty)$ between the horizon and asymptotically flat infinity, thus having the same structure as the Schwarzschild exterior region and the shape of a "diamond" $\Diamond$; (b) $r\in (r_- ,r_+)$ is a T-region between the horizons (the shape is the same $\Diamond$) and (c) $r\in (0,r_-)$ is again an R-region between the timelike singularity and the horizon. The timelike singularity turns the latter conformal diagram into a triangle, $\triangleright$ or $\triangleleft$. Gluing all the blocks together gives us the left diagram of Figs. |
| − | + | ||
| − | + | ||
| − | < | + | {|class="wikitable" style="margin: 1em auto 1em auto;" |
| − | + | |<gallery widths=300px heights=300px perrow=2 caption="Conformal diagrams for the generic (with no degenerate horizons) Reissner-Nordstrom black hole solution on the left and the extremal (with double horizon) Reissner-Nordstrom on the right. Blocks I and III are R-regions, blocks II are T-regions. Horizons are denoted by dashed lines, infinities by solid thick lines, singularities by wriggling curves. Both diagrams are infinitely continued up and down."> | |
| + | File:Conf-BH-ExampleRNv3.png | ||
| + | File:Conf-BH-ExampleRNeXv3.png | ||
| + | </gallery> | ||
| + | |} | ||
| − | + | 2) Due to degeneracy the T-region is absent, instead the two kinds of R-regions are separated by double horizons; the III-blocks on the right vanish, while on the left the singularity merges into a solid vertical line. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | < | + | 3) There can be up to three positive roots of $f$ in case $\Lambda>0$: $r_{-}<r_+<r_\Lambda$. Then there are four different conformal blocks:<br/> |
| − | + | a) block IV for the R-region between the timelike singularity and the inner horizon $r\in (0,r_-)$: $\triangleleft,\triangleright$;<br/> | |
| + | b) block III for the T-region between the two horizons $r\in(r_- ,r_+)$; it is the same as for Reissner-Nordstr\"{o}m: $\Diamond$;<br/> | ||
| + | c) block II for the R-region between the horizons $r\in (r_+ ,r_\Lambda)$; it differs from the exterior region of Reissner -Nordstrom or Schwarzschild by replacement of asymptotic infinity with another pair of horizons. The shape is the same, $\Diamond$, but the boundary now allows continuation across it in all directions;<br/> | ||
| + | d) block I for the T-region between the external (cosmological) horizon and the de-Sitter-like infinity. The structure of infinity is determined by $f(r)$ for large $r$, where the $\sim 1/r$ and $1/r^2$ terms can be neglected, so effectively we have the de Sitter spacetime. Thus the infinity is spacelike and represented by one horizontal line. The block is the triangle: $\triangle,\nabla$ (the same as the upper and lower sectors of the exact full de Sitter spacetime). | ||
| − | + | The full diagram is shown on Fig. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | {|class="wikitable" style="margin: 1em auto 1em auto;" | |
| − | + | |[[File:Conf-BH-ExampleGEN.png|center|thumb|365px|Conformal diagram for the Reissner-Nordstrom-de Sitter black hole solution. T-regions are shaded with darker grey. The diagram is infinitely continued up and down.]] | |
| − | + | |} | |
| − | + | </p> | |
| − | + | ||
| − | + | ||
| − | + | ||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 00:15, 4 February 2014
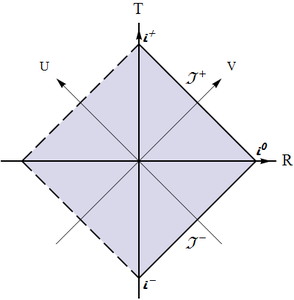
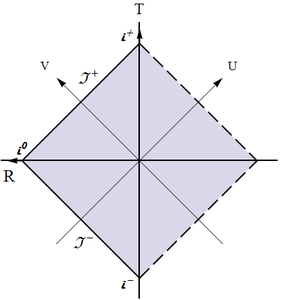
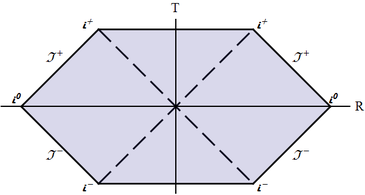
In the context of black hole spacetimes there are many subtly distinct notions of horizons, with the most useful being different from those used in cosmology. In particular, particle horizons do not play any role. The event horizon is defined not with respect to some selected observer, but with respect to all external observers: in an asymptotically flat spacetime* a future event horizon is the hypersurface which separates the events causally connected to future infinity and those that are not. Likewise the past event horizon delimits the events that are causally connected with past infinity or not. Another simple but powerful concept is the Killing horizon: in a spacetime with a Killing vector field $\xi^\mu$ it is a (hyper-)surface, on which $\xi^\mu$ becomes lightlike. We will see explicitly for the considered examples that the Killing horizons are in fact event horizons by constructing the corresponding conformal diagrams. In general, in the frame of GR a Killing horizon in a stationary spacetime is (almost) always an event horizon and also coincides with most other notions of horizons there are.
This section elaborates on the techniques of constructing conformal diagrams for stationary black hole solutions. The construction for the Schwarzschild black hole, or its variation, can be found in most textbooks on GR; for the general receipt see \cite{BrRubin}.
* Meaning the spacetime possesses the infinity with the same structure as that of Minkowski, which is important.
Schwarzschild-Kruskal black hole solution
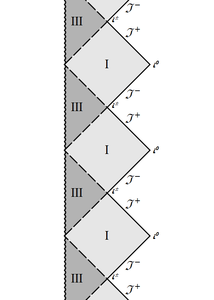
Problem 1: Schwarzschild exterior.
The simplest black hole solution is that of Schwarzschild, given by
\begin{equation}
ds^{2}=f(r)dt^2 -\frac{dr^2}{f(r)}-r^2 d\Omega^2,\qquad f(r)=1-\frac{r_g}{r},
\label{SchwBH}
\end{equation}
where $r_g$ is the gravitational radius, and $d\Omega^2$ is the angular part of the metric, which we will not be concerned with. The surface $r=r_g$ is the horizon. Focus for now only on the external part of the solution,
\[\big\{-\infty<t<+\infty,\;\;
r_g<r<+\infty)\big\}.\]
The general procedure of building a conformal diagram for the $(t,r)$ slice, as discussed in the cosmological context earlier, works here perfectly well, but needs one additional step in the beginning:
(a) use a new radial coordinate to bring the metric to conformally flat form;
(b) pass to null coordinates;
(c) shrink the ranges of coordinate values to finite intervals with the help of $\arctan$;
(d) return to timelike and spacelike coordinates.
Identify the boundaries of Schwarzschild's exterior region on the conformal diagram and compare it with Minkowski spacetime's.
(a) In terms of the new ("tortoise") coordinate
\begin{equation}
x=\int \frac{dr}{f(r)}=r+r_g \ln |r-r_g |
\end{equation}
we get
\begin{equation}
ds^2 =f(r(x))\big[dt^2 -dx^2\big].
\end{equation}
The horizon is pushed to infinity: $x\to -\infty$.
(b) Introduce
\begin{equation}
v=t+x,\quad u=t-x
\end{equation}
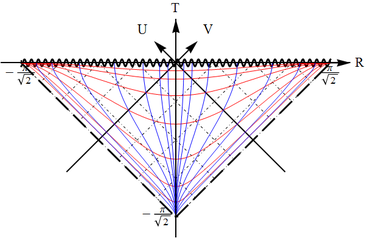
The horizon is at $v\to-\infty$ when $u=const$ (past horizon) and at $u\to -\infty$ when $v=const$ (future horizon). The asymptotically flat infinity is in the opposite direction: at $v\to+\infty$ when $u=const$ and at $u\to +\infty$ when $v=const$
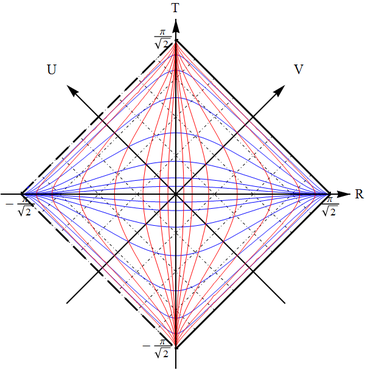
(c) Pass to $V=\arctan v$ and $U=\arctan u$; the horizon now becomes two lines at $V=-\pi/2$ and $U=-\pi/2$. The infinity is $V=+\pi/2$ and $U=+\pi/2$. The full exterior region is the square enclosed by those four lines.
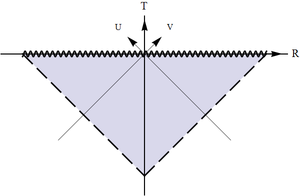
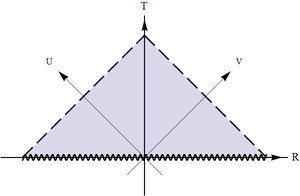
(d) Transformation to $T=V+U$, $R=V-U$ rotates this square by $\pi/4$ and this is the conformal diagram block that we need. There is a past and future horizon. Note that while past should be below and future above (we expect the spacetime to be oriented, so that the direction of future is always uniquely determined), there is no rule that says that the horizons must be on the left and infinities on the right. Thus there are two mirror-reflected variants, with the horizons on the left and on the right.
Problem 2: Schwarzschild interior.
The region $r\in (0,r_g)$ represents the black hole's interior, between the horizon $r=r_g$ and the singularity $r=0$. Construct the conformal diagram for this region following the same scheme as before.
(a) Which of the coordinates $(t,r)$ are timelike and which are spacelike?
(b) Is the singularity spacelike or timelike?
(c) Is the interior solution static?
The Schwarzschild black hole's interior is an example of the T-region, where $f(r)<0$, as opposed to the R-region, where $f(r)>0$.
The procedure is exactly the same as for the exterior region, the only thing that is different is the ranges of coordinates used and reversal of the timelike and spacelike coordinates:
(a) Now $t$ is spacelike and $r$ a timelike coordinate:
\begin{equation}
ds^2 =|f(r)|^{-1}dr^2 -|f(r)|dt^2 .
\end{equation}
(b) The singularity $r=0$ is therefore a spacelike one-dimensional object: one does not "reach" it or not, instead one lives until the specified time.
(c) The interior solution in not static, as the metric essentially depends on the new time coordinate $r$ (or $-r$).
The null coordinates then are (note the second sign)
\begin{equation}
v=t+x,\qquad u=x-t.
\end{equation}
The horizon is at $v\to -\infty$ when $u=const$ and at $u\to -\infty$ when $v=const$. After shrinking with $\arctan$ it is pulled to $v=-\pi/2$ and $u=-\pi/2$. The third part of the boundary, corresponding to the singularity $r=0$, is $v+u=const$.
Finally, we return to timelike and spacelike coordinates by introducing (there are two ways of choosing the sign)
\begin{equation}
T=\pm (v+u),\qquad R=V-U.
\end{equation}
The resulting conformal diagram is a 45 degrees right triangle with the right angle pointing either up (then the singularity is in the past) or down (then the singularity is in future). Note that we will know which of the horizons is past and which is future only when we match the blocks with the ones that have the corresponding infinities (although one can guess already where those will be).
Problem 3: Geodesic incompleteness and horizon regularity.
Consider radial motion of a massive particle and show that the exterior and interior parts of the Schwarzschild are not by themselves geodesically complete, i.e. particle's worldlines are terminated at the horizon at finite values of affine parameter. Show that, on the other hand, the horizon is not a singularity, by constructing the null coordinate frame, in which the metric on the horizon is explicitly regular.
The geodesic equation is obtained from normalization condition \begin{equation} \varepsilon^2=u^\mu u_\mu =f(r)\Big(\frac{dt}{d\lambda}\Big)^{2} -f^{-1}(r) \Big(\frac{dr}{d\lambda}\Big)^{2}, \end{equation} where $\varepsilon^2=0$ or $\varepsilon^2=1$ for null and timelike geodesics respectively, and conservation equation due to the Killing vector \begin{equation} E=u^\mu \xi_\mu =u_0 =f(r)\frac{dt}{d\lambda}, \label{BH-energy} \end{equation} and reads \begin{equation} \frac{d\lambda}{dr} =\Big[E^2 -f(r)\varepsilon^2 \Big]^{-1/2}. \label{BH-lambda} \end{equation} The integral $\lambda(r)$ converges at $r=r_g$, so the value of the affine parameter at the horizon is finite. In regard to regularity let us start from the exterior region. In terms of $u,v$ the metric has the overall conformal factor, which turns to zero at the horizon: \begin{equation} f(r)\sim (r-r_g)\sim e^{\ln (r-r_g)} \sim e^{x}\sim e^{(v-u)/2}, \end{equation} so in order to eliminate that, we just need to use new null coordinates $(u',v')$, such that the conformal factor in \begin{equation} ds^{2} \sim \Big(e^{-u/2}\frac{du}{du'}\Big) \sim \Big(e^{+v/2}\frac{dv}{dv'}\Big) du' dv' \end{equation} is finite and does not turn to zero. This is achieved e.g. by coordinate transformation to \begin{equation} u'=e^{u/2},\qquad v'=e^{-v/2}. \end{equation} After this one can carry out the second part of construction of the conformal diagram.
Problem 4: Piecing the puzzle.
Geodesic incompleteness means the full conformal diagram must be assembled from the parts corresponding to external and internal solutions by gluing them together along same values of $r$ (remember that each point of the diagram corresponds to a sphere). Piece the puzzle.
Note that a) there are two variants of both external and internal solutions' diagrams, differing with orientation and b) the boundaries of the full diagram must go along either infinities or singularities.
Starting from any one of the four pieces, there is only one way to assemble the diagram, and one has to use all the parts:
|
The horizon structure is very similar to that of full de Sitter spacetime in open slicing or "static" coordinates (the notions and properties of R- and T-regions apply equally well), while the structure of infinity is the same as that of Minkowski, and additionally there are singularities.
Finally, one could note that the form of the conformal block for the exterior solution was determined from the start. First, we have asymptotic flatness, therefore the Minkowski's structure of infinity. This is already half of the block's boundary.
Other spherically symmetric black holes
The Schwarzschild metric (\ref{SchwBH}) is the vacuum spherical symmetric solution of Einstein's equation. If we add some matter, we will obtain a different solution, e.g. Reissner-Nordstr\"{o}m for an electrically charged black hole. In all cases, spherical symmetry means that in appropriately chosen coordinate frame the metric takes the same form (\ref{SchwBH}), \begin{equation} ds^2 =f(\rho)dt^2 -\frac{d\rho^2}{f(\rho)}-r^2 (\rho)d\Omega^2 , \end{equation} but with some different function $f(\rho)$: one can always ensure that the metric functions have this form by choosing the appropriate radial coordinate\footnote{It is sometimes called the ``quasiglobal coordinate} $\rho$. The angular part $\sim d\Omega^2$ does not affect causal structure and conformal diagrams. The zeros $\rho=\rho^\star$ of $f(\rho)$ define the surfaces, which split the full spacetime into R- and T-regions and are the horizon candidates.
Problem 5: Killing horizons.
Consider radial geodesic motion of a massive or massless particle. Make use of the integral of motion $E=-u^\mu \xi_\mu$ due to the Killing vector and find $\rho (t)$ and $\rho(\lambda)$, where $\lambda$ is the affine parameter (proper time $\tau$ for massive particles)
(a) When is the proper time of reaching the horizon $\tau^\star =\tau (\rho^\star)$ finite?
(b) Verify that surface $\rho=\rho^\star$ is a Killing horizon
The formulas derived for Schwarzschild (\ref{BH-energy}) and (\ref{BH-lambda}) still work, just now $f(\rho)$ is not fixed.
(a)As for almost all particles $d\tau /d\rho$ stays bounded, the proper time of reaching the horizon candidate at $\rho=\rho^\star$ is finite if and only if $\rho^\star$ itself is finite. Otherwise we would have the "horizon" at infinite proper distance. It can be called a remote horizon, but extension across such a surface is not possible and not needed, as spacetime in that direction is already geodesically complete.
(b) The Killing vector that forms the horizon is $\xi_t =\partial_t$, its norm $|\xi_t |^2 =g_{tt}=f$. Thus $\rho=\rho^\star$ is indeed a Killing horizon by definition.
Problem 6: Extension across horizons.
Let us shift the $\rho$ coordinate so that $\rho^\star =0$, and assume that \begin{equation} f(\rho)=\rho^{q}F(\rho),\qquad q\in\mathbb{N}, \end{equation} where $F$ is some analytic function, with $F(0)\neq 0$. Suppose we want to introduce a new radial "tortoise" coordinate $x$, such that the two-dimensional part of the metric in terms of $(t,x)$ has the conformally flat form: \begin{equation} ds^2_2 =f(\rho(x))\big[dt^2 -dx^2 \big]. \end{equation}
(a)What is the asymptotic form of relation $\rho (x)$?
(b) Rewrite the metric in terms of null coordinates
\begin{equation}
V=t+x,\qquad W=t-x.
\end{equation}
Where is the horizon in terms of these coordinates? Is there only one?
(c) Suppose we pass to new null coordinates $V=V(v)$ and $W=W(w)$. What conditions must be imposed on functions $V(v)$ and $W(w)$ in order for the mixed map $(v,W)$ to cover the past horizon and the map $(w,V)$ to cover the future horizon without singularities?
(a) Integrating $dx=f^{-1}d\rho$, one obtains
\begin{equation}
\rho\sim \left\{\begin{array}{l}
e^{xF(0)},\quad \text{for}\quad q=1,\\
|x|^{-1/(q-1)}\quad\text{for}\quad q>1 .
\end{array}\right.
\end{equation}
We see that $x\to -\infty$ at the horizon. It converges for $q<1$, but in this case one can show that the Kretschmann scalar $R_{\mu\nu\rho\sigma}R^{\mu\nu\rho\sigma}$ diverges, so this is not a horizon but a singularity.
(b) $ds^2 =f \; dV\;dW$; the horizon is at $x\to -\infty$ while $t$ is fixed, so in terms of $V$ and $W$ it is split into two parts: the future horizon at $V\to -\infty$ while $W$ is fixed, and the past horizon at $W\to +\infty$ while $V$ is fixed.
(c) Near the past horizon in terms of $(v,W)$ the metric takes form
\begin{equation}
ds^2 =\Big(f \frac{dW}{dw}\Big)\; dV\; dw,
\end{equation}
while $W\approx -x$, so for it to be regular there we need
\begin{equation}
\frac{dW}{dw}\sim f^{-1}\sim \rho^{q} \sim \left\{
\begin{array}{l}
|x|^{(1-q)/q}\sim W ^{(1-q)/q}\quad\text{for}\quad q>1 ,\\
e^{xF(0)}\sim e^{-WF(0)}\quad\text{for}\quad q= 1,
\end{array}\right.
\end{equation}
and after integrating
\begin{equation}
W\sim \left\{\begin{array}{l}
w^{1-q}\quad\text{for}\quad q>1 ,\\
\ln w\quad\text{for}\quad q= 1.
\end{array}\right.
\end{equation}
The same way the asymptotic relation $V(v)$ is found near the future horizon.
Thus a horizon candidate $\rho=\rho^\star$ is defined by condition $f(\rho^\star)=0$. If $\rho^\star =\pm\infty$, then the proper time of reaching it diverges, so it is not a horizon, but an infinitely remote boundary of spacetime. It can be a remote horizon if $x^\star =\pm \infty$. In case $x^\star =O(1)$ the candidate is not a horizon, but a singularity, so again there is no continuation. An asymptotically flat spacetime by definition has the same structure of infinity as that of Minkowski spacetime; in general this is not always the case---recall the de Sitter and other cosmological spacetimes.
Problem 7: Infinities, horizons, singularities.
Draw the parts of conformal diagrams near the boundary that correspond to the limiting process
\begin{equation}
\rho\to\rho_0 ,\qquad |\rho_0|<\infty,
\end{equation}
under the following conditions:
(a) spacelike singularity: $f(\rho_0)>0$, $|x_0 |<\infty$;
(b) timelike singularity: $f(\rho_0)<0$, $|x_0 |<\infty$;
(c) asymptotically flat infinity: $\rho_0 =\pm \infty$, $f(\rho)\to f_0>0$;
(d) a horizon in the R region: $f(\rho)\to +0$, $|x_0 |\to \infty$;
(e) a horizon in the T region: $f(\rho)\to -0$, $|x_0 |\to \infty$;
(f) remote horizon in a T-region: $\rho_0 =\pm \infty$, $f(\rho)\to -<0$;
Remember that any spacelike line can be made "horizontal" and any timelike one can be made "vertical" by appropriate choice of coordinates.
(a) Horizontal line, approached either from above or from below; it acts as the boundary of spacetime -- there is no continuation across (see Fig.);
(b) Vertical line, approached either from the left or from the right; as it is singular, there is again no continuation (see Fig.);
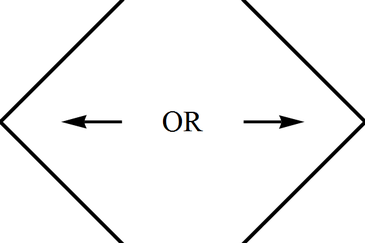
(c) This is the infinitely remote part of Minkowski spacetime, from future infinity, to future null infinity, to spacelike infinity, to past null infinity, and finally to past infinity; it can constitute either the left or the right boundary of a conformal block and has the shape of "$>$" or "$<$" (see Fig. \ref{Conf-BH-InfMink});
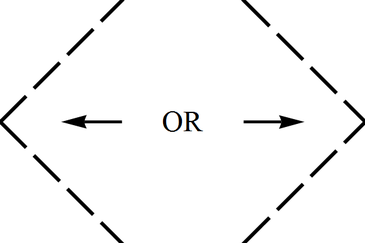
(d) The same as the Schwarzschild horizon as approached from the exterior region: the two sides of a triangle pointed left "$<$" or right "$<$" and approached from the inside; thus the shape is the same as above, but now the horizon allows continuation across (see Fig.);
(e) The same as Schwarzschild horizon as approached from the interior region: two sides of a triangle pointed up "$\wedge$" or down "$\vee$" and approached from the inside (see Fig.).
(f) Two diagonal lines -- a corner of a triangle, -- pointed up or down, and approached from the inside. Thus the shape is the same as in the previous case, "$\wedge$" or "$\vee$"; the difference is that now there is no continuation across (see Fig.).
For arbitrary $f(\rho)$ we can
1) split the full spacetime into regions between the zeros $\rho_i$ of $f(\rho)$;
2) draw for each region the conformal diagram, which is a square $\Diamond$ or half of it $\triangle$, $\nabla$, $\triangleleft$, $\triangleright$;
3) glue the pieces together along the horizons $\rho=\rho_i$, while leaving singularities and infinities as the boundary.
Problem 8: Examples.
Draw the conformal diagrams for the following spacetimes:
1) Reissner-Nordstrom charged black hole: \begin{equation} f(r)=1-\frac{r_g}{r}+\frac{q^2}{r^2}, \qquad 0<q<r_{g},\qquad r>0; \end{equation}
2) Extremal Reissner-Nordstr\"{o}m charged black hole \begin{equation} f(r)=\Big(1-\frac{q}{r}\Big)^2, \qquad q>0,\qquad r>0; \end{equation}
3) Reissner-Nordstrom-de Sitter charged black hole with cosmological constant (it is not asymptotically flat, as $f(\infty)\neq 1$) \begin{equation} f(r)=1-\frac{r_g}{r}+\frac{q^2}{r^2}-\frac{\Lambda r^2}{3}\qquad q,\Lambda>0; \end{equation} analyze the special cases of degenerate roots.
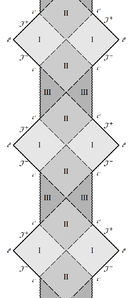
1) In the generic case there are two positive roots $+\infty>r_+ >r_- >0$, which give horizons, while $r=0$ is a singularity. This gives us three regions between the roots: (a) $r\in(r_+ ,+\infty)$ between the horizon and asymptotically flat infinity, thus having the same structure as the Schwarzschild exterior region and the shape of a "diamond" $\Diamond$; (b) $r\in (r_- ,r_+)$ is a T-region between the horizons (the shape is the same $\Diamond$) and (c) $r\in (0,r_-)$ is again an R-region between the timelike singularity and the horizon. The timelike singularity turns the latter conformal diagram into a triangle, $\triangleright$ or $\triangleleft$. Gluing all the blocks together gives us the left diagram of Figs.
|
2) Due to degeneracy the T-region is absent, instead the two kinds of R-regions are separated by double horizons; the III-blocks on the right vanish, while on the left the singularity merges into a solid vertical line.
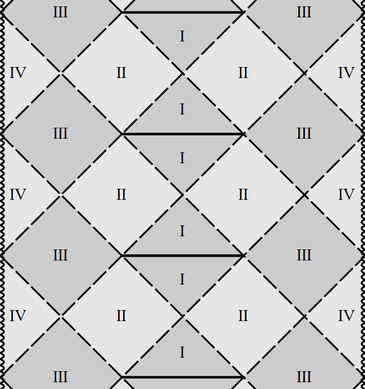
3) There can be up to three positive roots of $f$ in case $\Lambda>0$: $r_{-}<r_+<r_\Lambda$. Then there are four different conformal blocks:
a) block IV for the R-region between the timelike singularity and the inner horizon $r\in (0,r_-)$: $\triangleleft,\triangleright$;
b) block III for the T-region between the two horizons $r\in(r_- ,r_+)$; it is the same as for Reissner-Nordstr\"{o}m: $\Diamond$;
c) block II for the R-region between the horizons $r\in (r_+ ,r_\Lambda)$; it differs from the exterior region of Reissner -Nordstrom or Schwarzschild by replacement of asymptotic infinity with another pair of horizons. The shape is the same, $\Diamond$, but the boundary now allows continuation across it in all directions;
d) block I for the T-region between the external (cosmological) horizon and the de-Sitter-like infinity. The structure of infinity is determined by $f(r)$ for large $r$, where the $\sim 1/r$ and $1/r^2$ terms can be neglected, so effectively we have the de Sitter spacetime. Thus the infinity is spacelike and represented by one horizontal line. The block is the triangle: $\triangle,\nabla$ (the same as the upper and lower sectors of the exact full de Sitter spacetime).
The full diagram is shown on Fig.