Difference between revisions of "Dark Matter Halo"
(→Problem 5) |
|||
| (8 intermediate revisions by the same user not shown) | |||
| Line 25: | Line 25: | ||
<div id="halo_model"></div> | <div id="halo_model"></div> | ||
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | === Problem | + | === Problem 2 === |
Build the model of the spherically symmetric dark halo density corresponding to the observed galactic rotation curves. | Build the model of the spherically symmetric dark halo density corresponding to the observed galactic rotation curves. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
| Line 35: | Line 35: | ||
The conditions are satisfied by the following function | The conditions are satisfied by the following function | ||
\[ | \[ | ||
| − | \rho (r) = \rho _0 \frac | + | \rho (r) = \rho _0 \frac{r_c^2 + r_0^2}{r_c^2 + r^2} |
\] | \] | ||
where $\rho _0 = \rho (r_0 )$ is the local halo density in vicinity of the Sun (if it concerns the dark halo in Milky Way) at $r = r_0 $ and $r_c$ is the core radius, inside which the density grows (with decreasing $r$ ) not faster than $1/r^2 $ and goes to constant, thus providing the linear growth of the rotation curves) at small $r.$</p> | where $\rho _0 = \rho (r_0 )$ is the local halo density in vicinity of the Sun (if it concerns the dark halo in Milky Way) at $r = r_0 $ and $r_c$ is the core radius, inside which the density grows (with decreasing $r$ ) not faster than $1/r^2 $ and goes to constant, thus providing the linear growth of the rotation curves) at small $r.$</p> | ||
| Line 45: | Line 45: | ||
<div id="DM16"></div> | <div id="DM16"></div> | ||
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | === Problem | + | |
| + | === Problem 3 === | ||
In frames of the halo model considered in the previous problem determine the local dark matter density $\rho_0$ basing on the given rotation velocities of satellite galaxies at the outer border of the halo $v_\infty\equiv v(r\rightarrow\infty)$ and in some point $r_0$. | In frames of the halo model considered in the previous problem determine the local dark matter density $\rho_0$ basing on the given rotation velocities of satellite galaxies at the outer border of the halo $v_\infty\equiv v(r\rightarrow\infty)$ and in some point $r_0$. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
| Line 52: | Line 53: | ||
<p style="text-align: left;">Let some satellite galaxy orbits on the distance $r$ from the center of the main galaxy of mass $M\left( r \right)$ with velocity $v (r)$, then | <p style="text-align: left;">Let some satellite galaxy orbits on the distance $r$ from the center of the main galaxy of mass $M\left( r \right)$ with velocity $v (r)$, then | ||
\[ | \[ | ||
| − | \frac | + | \frac{v^2}{r} = G\frac{M(r)}{r^2}. |
\] | \] | ||
As | As | ||
| Line 59: | Line 60: | ||
\] | \] | ||
then substitution of the expression for $\rho | then substitution of the expression for $\rho | ||
| − | (r)$ (see | + | (r)$ (see [[#11_14|problem]]) one obtains |
\[ | \[ | ||
| − | v^2 (r) = 4\pi G\frac{1}{r}\int_0^r {r'^2 \rho \left( {r'} | + | v^2 (r) = 4\pi G\frac{1}{r}\int_0^r {r'^2 \rho \left( {r'}\right)dr'} = 4\pi G\rho _0 \left( {r_c^2 + r_0^2 } \right)\left[ |
| − | \right)dr'} = 4\pi G\rho _0 \left( {r_c^2 + r_0^2 } \right)\left[ | + | {1 - \left( \frac{r_c}{r} \right)arctg\left( \frac{r}{r_0 } |
| − | {1 - \left( | + | |
\right)} \right], | \right)} \right], | ||
\] | \] | ||
so it follows that | so it follows that | ||
\[ | \[ | ||
| − | v_\infty ^2 = v^2 \left( {r \to \infty } \right) = 4\pi G\rho _0 | + | v_\infty ^2 = v^2 \left( {r \to \infty } \right) = 4\pi G\rho _0\left( {r_c^2 + r_0^2 } \right) |
| − | \left( {r_c^2 + r_0^2 } \right) | + | |
\] | \] | ||
and | and | ||
\[ | \[ | ||
| − | \rho _0 = \frac | + | \rho _0 = \frac{v_\infty ^2}{4\pi G\left( {r_c^2 + r_0^2 }\right)}. |
| − | \right) | + | |
\] | \] | ||
From the other hand the core radius $r_c $ can be determined from the relation | From the other hand the core radius $r_c $ can be determined from the relation | ||
\[ | \[ | ||
| − | \left( | + | \left( \frac{r_c}{r_0} \right)arctg\left( \frac{r_0}{r_c} \right) = 1 - \frac{v^2 \left( {r_0 }\right)}{v_\infty ^2}. |
| − | + | ||
| − | \right) | + | |
\] | \] | ||
Thus the local density and the core radius can be determined as soon as the rotation velocities $v\left( {r_0 } | Thus the local density and the core radius can be determined as soon as the rotation velocities $v\left( {r_0 } | ||
| Line 92: | Line 88: | ||
<div id="11_17"></div> | <div id="11_17"></div> | ||
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | === Problem | + | |
| − | For the halo model considered in | + | === Problem 4 === |
| + | For the halo model considered in [[#halo_model|problem]] about halo model obtain the dependencies $\rho(r)$ and $v(r)$ in terms of $\rho_0$ and $v_\infty$. Plot the dependencies $\rho(r)$ and $v(r)$. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;">\[\rho \left( r \right) = \frac | + | <p style="text-align: left;">\[\rho \left( r \right) = \frac{v_\infty ^2}{4\pi G}\frac{1}{r_c^2 + r^2} ;\quad v(r) = v_\infty \sqrt{ 1 - \frac{r_c }{r} \arctan{\frac{r}{r_c}}} \] |
| − | + | ||
| − | + | ||
| − | + | ||
For $v_\infty = 220\mbox{km/s},\;r_c = 2.6\mbox{kpc},\,r_0 = 8\mbox{kpc}$ | For $v_\infty = 220\mbox{km/s},\;r_c = 2.6\mbox{kpc},\,r_0 = 8\mbox{kpc}$ | ||
| Line 116: | Line 110: | ||
<div id=""></div> | <div id=""></div> | ||
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | === Problem | + | |
| + | === Problem 5 === | ||
Many clusters are sources of X-ray radiation. It is emitted by the hot intergalactic gas filling the cluster volume. Assuming that the hot gas ($kT\approx10keV$) is in equilibrium in the cluster with linear size $R=2.5Mpc$ and core radius $r_c=0.25Mpc$, estimate the mass of the cluster. | Many clusters are sources of X-ray radiation. It is emitted by the hot intergalactic gas filling the cluster volume. Assuming that the hot gas ($kT\approx10keV$) is in equilibrium in the cluster with linear size $R=2.5Mpc$ and core radius $r_c=0.25Mpc$, estimate the mass of the cluster. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
| Line 133: | Line 128: | ||
M(r)=-\frac{rkT}{Gm_p}\frac{d\ln\rho}{d\ln r}. | M(r)=-\frac{rkT}{Gm_p}\frac{d\ln\rho}{d\ln r}. | ||
$$ | $$ | ||
| − | Using results of the | + | Using results of the [[#DM16|problem]] |
$$ | $$ | ||
| − | \rho(r) = \frac | + | \rho(r) = \frac{v_\infty ^2}{4\pi G\left( {r_c^2 + r }\right)}, |
| − | \right) | + | |
$$ | $$ | ||
one obtains | one obtains | ||
Latest revision as of 10:13, 4 October 2012
Problem 1
Estimate the local density of the dark halo in the vicinity of the Earth, assuming that its density decreases as $\rho_g=C/r^2$.
\[M_g = 4\pi \int_0^{R_g } {\rho_g (r)} r^2 dr = 4\pi CR_g\Rightarrow\rho_g = \frac{M_g}{4\pi R_g r^2}.\] For $M_g\sim 10^{11} M_ \odot ,\;R_g \sim 10\mbox{kpc},\;r\sim 6.7\mbox{kpc}$ and assuming that the dark matter dominates in the halo, one obtains \[\rho _g \approx \rho _{_{DM}} \sim 10^{ - 25} \mbox{g/cm}^3\approx 0.2\mbox{ GeV/cm}^3.\]
Problem 2
Build the model of the spherically symmetric dark halo density corresponding to the observed galactic rotation curves.
The simplest halo model is the isothermic spherically symmetric one. The radial profile of the density in the model is restricted only by the observed rotation curves. This restriction leads to the following requirements for radial dependence of the density:
a) it must provide linear growth of the rotation curves at small distances.
b) it must follow as $1/r^2 $ for large distances, thus providing flat rotation curves.
The conditions are satisfied by the following function
\[
\rho (r) = \rho _0 \frac{r_c^2 + r_0^2}{r_c^2 + r^2}
\]
where $\rho _0 = \rho (r_0 )$ is the local halo density in vicinity of the Sun (if it concerns the dark halo in Milky Way) at $r = r_0 $ and $r_c$ is the core radius, inside which the density grows (with decreasing $r$ ) not faster than $1/r^2 $ and goes to constant, thus providing the linear growth of the rotation curves) at small $r.$
Problem 3
In frames of the halo model considered in the previous problem determine the local dark matter density $\rho_0$ basing on the given rotation velocities of satellite galaxies at the outer border of the halo $v_\infty\equiv v(r\rightarrow\infty)$ and in some point $r_0$.
Let some satellite galaxy orbits on the distance $r$ from the center of the main galaxy of mass $M\left( r \right)$ with velocity $v (r)$, then \[ \frac{v^2}{r} = G\frac{M(r)}{r^2}. \] As \[ M(r) = 4\pi \int_0^r {r'^2 \rho \left( {r'} \right)dr'}, \] then substitution of the expression for $\rho (r)$ (see problem) one obtains \[ v^2 (r) = 4\pi G\frac{1}{r}\int_0^r {r'^2 \rho \left( {r'}\right)dr'} = 4\pi G\rho _0 \left( {r_c^2 + r_0^2 } \right)\left[ {1 - \left( \frac{r_c}{r} \right)arctg\left( \frac{r}{r_0 } \right)} \right], \] so it follows that \[ v_\infty ^2 = v^2 \left( {r \to \infty } \right) = 4\pi G\rho _0\left( {r_c^2 + r_0^2 } \right) \] and \[ \rho _0 = \frac{v_\infty ^2}{4\pi G\left( {r_c^2 + r_0^2 }\right)}. \] From the other hand the core radius $r_c $ can be determined from the relation \[ \left( \frac{r_c}{r_0} \right)arctg\left( \frac{r_0}{r_c} \right) = 1 - \frac{v^2 \left( {r_0 }\right)}{v_\infty ^2}. \] Thus the local density and the core radius can be determined as soon as the rotation velocities $v\left( {r_0 } \right)$ and $v_\infty $ are measured.
Problem 4
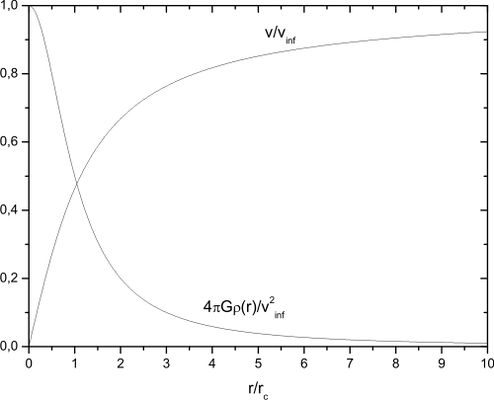
For the halo model considered in problem about halo model obtain the dependencies $\rho(r)$ and $v(r)$ in terms of $\rho_0$ and $v_\infty$. Plot the dependencies $\rho(r)$ and $v(r)$.
\[\rho \left( r \right) = \frac{v_\infty ^2}{4\pi G}\frac{1}{r_c^2 + r^2} ;\quad v(r) = v_\infty \sqrt{ 1 - \frac{r_c }{r} \arctan{\frac{r}{r_c}}} \] For $v_\infty = 220\mbox{km/s},\;r_c = 2.6\mbox{kpc},\,r_0 = 8\mbox{kpc}$ one obtains $\rho_0 \approx 5 \times 10^{ - 25} \mbox{g/cm}^3 \approx 0.3\,\mbox{GeV/cm}^3 $. The dependencies $\rho \left( r \right)$ and $v(r)$ are plotted on Figure.
Problem 5
Many clusters are sources of X-ray radiation. It is emitted by the hot intergalactic gas filling the cluster volume. Assuming that the hot gas ($kT\approx10keV$) is in equilibrium in the cluster with linear size $R=2.5Mpc$ and core radius $r_c=0.25Mpc$, estimate the mass of the cluster.
Equation of hydrostatic equilibrium reads: $$ \frac 1{\rho}\frac {dp}{dr}=-\frac {GM(r)}{r^2}, $$ where $p$ is pressure, and $\rho$ is density of the ideal gas with the state equation $p=nkT$, where $n$ is the concentration of the gas $n=\rho/m_p$. Let us assume the isothermic temperature distribution $T=const,$ then $$ \frac{kT}{m_p\rho}\frac{d\rho}{dr}=-\frac {GM(r)}{r^2}, $$ and it follows that $$ M(r)=-\frac{rkT}{Gm_p}\frac{d\ln\rho}{d\ln r}. $$ Using results of the problem $$ \rho(r) = \frac{v_\infty ^2}{4\pi G\left( {r_c^2 + r }\right)}, $$ one obtains $$ M(r)=2\frac{rkT}{Gm_p}\frac{r^2}{r_c^2 + r }\approx 10^{16}M_{\odot}. $$