Difference between revisions of "Friedman-Lemaitre-Robertson-Walker (FLRW) metric"
(→Problem 1.) |
|||
| Line 10: | Line 10: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;">[[Image:2_16.jpg|thumb|500px]]</p> | + | <p style="text-align: left;">[[Image:2_16.jpg|thumb|500px]] |
| + | When the radius of the sphere grows with time as $a(t)$, the angle $\theta_{AB}$ between two arbitrary points $A$ and $B$ is constant. Therefore the distance between the points changes as | ||
| + | \[r_{AB}(t) = a(t)\theta _{AB}\] | ||
| + | and relative velocity is | ||
| + | \[v_{AB} = \dot r_{AB} | ||
| + | = \dot a(t)\theta _{AB} = \frac{\dot a}{a}r_{AB}.\] | ||
| + | On denoting | ||
| + | \[\frac{\dot a}{a} \equiv H(t),\] | ||
| + | one recovers the Hubble's law. | ||
| + | </p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 25: | Line 34: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Suppose $a=a(r,t)$. Then we differentiate $r_{AB}$ with respect to time to obtain |
| + | \[V_{AB}=\chi_{AB}\; \dot{a} | ||
| + | =r_{AB}\frac{\dot{a}}{a},\] | ||
| + | so it is easy to see that | ||
| + | \[H=\frac{\dot{a}}{a},\] | ||
| + | where the scale factor $a(r,t)$ can be expressed in terms of the Hubble's parameter as | ||
| + | \[a(t) = a_{0}\exp \left( \int H(t)dt \right),\] | ||
| + | and thus it can depend solely on time. | ||
| + | |||
| + | The scale factor represents an analogue of radius of the two-dimensional sphere from the previous problem. Its normalization is arbitrary and it determines the unit of length in the comoving reference frame. If the normalization is fixed then the scale factor determines distance between objects or observers at a given moment of time. The comoving distance between them $\chi_{AB}$ is analogous to the angle $\theta_{AB}$ from the previous problem and it can be treated as a Lagrangian (comoving) coordinate of the point $B$ in the reference frame centered in point $A$.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 51: | Line 69: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">IMAGE!!! |
| + | Spatial isotropy implies spherical symmetry. In this case the spatial line element in comoving coordinates $(\chi,\vartheta,\phi)$ takes the form: | ||
| + | \[dl ^2 | ||
| + | = d\chi^2 + f^2 (\chi) | ||
| + | \left( d\vartheta ^2 | ||
| + | + \sin^2\vartheta d\phi ^2 \right),\] | ||
| + | where $f(\chi)$ is a real-valued function which must satisfy the condition $f(\chi)\approx \chi $ at $\chi \rightarrow 0$ in the case of non-singular metrics. | ||
| + | |||
| + | Let us fix the angle $\theta$ and consider the triangle $DGE$ in the plane $\theta=\pi/2$, shown on Fig.~\ref{fig:G}. Here $DH=HE=\chi$, $HA=\delta$, the distance $DE$ and angle $\gamma$ are assumed to be small. Angles $GDH$ and $GEH$ are both equal to $\gamma$ due to homogeneity and isotropy. Note also that \begin{equation}\label{21-1} | ||
| + | EF \simeq EF' = f( 2\chi )\gamma = f( \chi)\beta | ||
| + | \end{equation} | ||
| + | and | ||
| + | \begin{equation}\label{21-2} | ||
| + | AC = \gamma f(\chi+\delta) = AB + BC | ||
| + | =\gamma f(\chi-\delta) + \beta f(\delta). | ||
| + | \end{equation} | ||
| + | |||
| + | Using (\ref{21-1}), we exclude the ratio $\beta /\gamma $ from (\ref{21-2}) and in the limit $\delta \to 0$ obtain the equation | ||
| + | \begin{equation}\label{21-3} | ||
| + | \frac{df}{d\chi} | ||
| + | =\frac{f( 2\chi)}{2f(\chi)}\cdot | ||
| + | \frac{df}{d\chi}\Big|_{\chi=0}. | ||
| + | \end{equation} | ||
| + | We are interested in its solutions which satisfy $df(\chi)/d\chi\big|_{\chi=0}=1$. It is easy to verify that functions $\chi$, $\sin\chi$ and $\sinh\chi$ are all such solutions. We note also, that if $f(\chi)$ is a solution of the equation (\ref{21-3}), then $f(\chi/\alpha)$, where $\alpha$ is an arbitrary constant, is also a solution. If we assume that $f$ is analytic and expand it into series over $\chi$, it is easy to show that up to rescaling $\chi\to \chi/\alpha$ all the possible solutions of (\ref{21-3}) are given by the following three: | ||
| + | \[f(\chi)=\Sigma(\chi)=\left\{\begin{array}{l} | ||
| + | \sin \chi\\ \chi\\ \sinh \chi\;. | ||
| + | \end{array}\right.\] | ||
| + | Without violation of homogeneity and isotropy, the line element of the three-dimensional space can be multiplied by an arbitrary function of time, and thus the general form of the spacetime metric is | ||
| + | \[ds^2=dt^2-a^2(t) | ||
| + | \left\{ d\chi^2+f^2(\chi) | ||
| + | (d\theta^2+\sin^2\theta d\varphi^2)\right\}.\]</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 57: | Line 105: | ||
<div id="equ20"></div> | <div id="equ20"></div> | ||
| − | |||
=== Problem 4. === | === Problem 4. === | ||
Show that the FLRW metric (\ref{FLRW1}) can be presented in the form | Show that the FLRW metric (\ref{FLRW1}) can be presented in the form | ||
| Line 69: | Line 116: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;"> In each of the three cases we introduce a new variable |
| + | \[r\equiv \Sigma(\chi)=\left\{\begin{array}{lcl} | ||
| + | \sin\chi \\%\qquad \; \; k=+1\\ | ||
| + | \chi \\%\qquad \qquad k=0\\ | ||
| + | \sinh\chi \\%\qquad k=-1\\ | ||
| + | \end{array}\right.,\qquad | ||
| + | dr=\left\{\begin{array}{lcl} | ||
| + | \cos\chi d\chi\\ | ||
| + | d\chi\qquad\\ | ||
| + | \cosh\chi d\chi\\ | ||
| + | \end{array},\right.\] | ||
| + | so that | ||
| + | \[ d\chi^2 =\frac{dr^2}{1-kr^2}, | ||
| + | \quad\text{where}\quad | ||
| + | k=\left\{\begin{array}{rcl} | ||
| + | +1&\quad\text{if}\quad& r=\sin\chi \\ | ||
| + | 0&\quad\text{if}\quad& r=\chi\\ | ||
| + | -1&\quad\text{if}\quad& r=\sinh\chi | ||
| + | \end{array}\right.\] | ||
| + | and finally obtain | ||
| + | \[ ds^2=dt^2-a^2(t) \left\{ | ||
| + | \frac{dr^2}{1-kr^2}+r^2 | ||
| + | (d\theta^2+\sin^2\theta d\varphi^2) \right\}.\]</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 75: | Line 144: | ||
<div id="equ57"></div> | <div id="equ57"></div> | ||
| − | |||
=== Problem 5. === | === Problem 5. === | ||
Show that only the sign of spatial curvature has physical meaning, as renormalization of the scale factor rescales the curvature. | Show that only the sign of spatial curvature has physical meaning, as renormalization of the scale factor rescales the curvature. | ||
| Line 81: | Line 149: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Suppose we have metric |
| + | \[ ds^2=dt^2-\alpha^2(t) \Big\{ | ||
| + | \frac{dr^2}{1-k \beta^{2}r^2}+r^2 | ||
| + | (d\theta^2+\sin^2\theta d\varphi^2) \Big\},\] | ||
| + | where $\beta=const$. Then we can always introduce $\chi=\beta r$ and $a(t)=\alpha(t)/\beta$ and bring the metric to the canonical form (\ref{FLRW2}). Note, that this has sense only if $k\neq 0$.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 92: | Line 164: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">It follows from the fact that in the case of a flat Universe there is no spatial scale to normalize the scale factor by.</p> |
</div> | </div> | ||
</div> | </div> | ||
| Line 103: | Line 175: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">In the case of closed Universe the spatial line element takes the form |
| + | \[dl^2=a^2(t)\left\{d\chi^2 | ||
| + | +\sin^{2}\chi(d\theta^2+\sin^2\theta d\phi^2)\right\}.\] | ||
| + | Then the area of a sphere with radius $\chi$, circumscribed around the center, equals to | ||
| + | \[s(\chi)= 4\pi a^2(t) \sin^2(\chi),\] | ||
| + | and the equator's length is | ||
| + | \[l=2\pi a(t) \sin(\chi).\] | ||
| + | It can be seen from the relation for $s(\chi)$ that $s$ reaches maximum $s_{max} = 4\pi a^2(t)$ at $\chi=\pi/2$, then decreases and turns again to zero at $\chi = \pi$. Thus the value $\chi = \pi$ gives the maximum value the coordinate $\chi$ can take. | ||
| + | |||
| + | The volume inside a sphere of radius $\chi$ equals to | ||
| + | \[V =\int\limits_0^{\chi} s(\chi') a(t) d\chi' | ||
| + | = 4\pi a^3(t) \int\limits_0^{\chi} \sin^2(\chi') d\chi' | ||
| + | = 4\pi a^3(t)\left(\frac 1 2 \chi | ||
| + | - \frac 1 4 \sin(2\chi) \right)\] | ||
| + | and monotonically grows with $\chi$. At $\chi = \pi$ one obtains the total volume of the closed world: | ||
| + | \[V_{universe} = 2 \pi^2 a^3.\]</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 114: | Line 201: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">A charge is a source of electric field. In Euclidean space the electric field lines begin on a charge and then either end on a charge of the opposite sign or go to infinity. However there is no infinity in the closed world. |
| + | |||
| + | Let us fix some arbitrary electric field distribution $\vec E$ in the closed world and find the corresponding charge density $\varepsilon _e$ using the equation $ \mbox{div}\vec E = 4\pi \varepsilon _e$. It will always turn out that the total charge equals to zero, i.e. $Z = \int \varepsilon_e dV = 0$, as in the absence of infinity the lines of force always start from one charge and necessarily end on another charge of the opposite sign, which thus neutralizes the former charge.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 125: | Line 214: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">In an expanding Universe the physical distance $D$ between the observer in the origin of reference frame and a receding galaxy is measured along the surface of constant time $dt=0$. If one considers the radial distance then $d\theta=d\phi=0$, so |
| + | \[D(t) = a(t)\chi.\] | ||
| + | Evaluating time derivative and taking into account that $\dot \chi = 0,$ one obtains | ||
| + | \[ V \equiv \frac{dD(t)}{dt} = \dot a(t)\chi | ||
| + | = \frac{\dot a(t)}{a(t)}a(t)\chi = H(t)D.\]</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 138: | Line 231: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">On substitution $dt=a d\eta$ we get |
| + | \begin{equation}\label{FLRWconformal} | ||
| + | d{s^2} = a^2(\eta ) | ||
| + | \Big\{ d\eta ^2 - \big[ d\chi ^2 | ||
| + | + \Sigma ^2(\chi )\left( d\theta ^2 + | ||
| + | \sin^2\theta\; d\varphi ^2\right)\big]\Big\}. | ||
| + | \end{equation} | ||
| + | Then | ||
| + | \[\dot{a}=\frac{da}{dt}=\frac{da}{ad\eta} | ||
| + | =\frac{d\,\ln a}{d\eta}.\]</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 149: | Line 251: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">In comoving coordinates the FLRW metric has the form |
| + | \[d{s^2} = d{t^2} - a^2(t)\delta _{ij}dx^{i}dx^{j},\] | ||
| + | then the change of variables $dt=a(\eta)d\eta$ leads to metric | ||
| + | \[ds^2 = a^2(\eta ) | ||
| + | \left[ d\eta ^2 - \delta _{ij}dx^idx^j \right],\] | ||
| + | and it follows that $g_{\mu \nu } = a^2(\eta )\eta _{\mu \nu }$, where $\eta _{\mu \nu }$ is the Minkowski metric.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 155: | Line 262: | ||
<div id="equ66n"></div> | <div id="equ66n"></div> | ||
| − | |||
=== Problem 12. === | === Problem 12. === | ||
Consider an arbitrary function of time $f(t)$ and express $\dot{f}$ and $\ddot{f}$ in terms of derivatives with respect to conformal time. | Consider an arbitrary function of time $f(t)$ and express $\dot{f}$ and $\ddot{f}$ in terms of derivatives with respect to conformal time. | ||
| Line 161: | Line 267: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Let us denote differentiation with respect to time $t$ by a dot, and with respect to conformal time $\eta$ by a prime. Then |
| + | \begin{align*} | ||
| + | &\dot f = \frac{f'}{a};\\ | ||
| + | &\ddot f=\frac{f''}{a^2} - \frac{f'a'}{a^3} | ||
| + | = \frac{f''-\mathcal{H} f'}{a^2}, | ||
| + | \quad\text{where}\quad | ||
| + | \mathcal{H}\equiv \frac{a'}{a} | ||
| + | \end{align*} | ||
| + | is the Hubble' constant in conformal time.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 172: | Line 286: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">A worldline of a photon is defined by equation $d{s^2} =0$. It is sufficient to consider only radial trajectories with the observer in the origin of coordinate frame. Using the metrics (\ref{FLRWconformal}), IT |
| + | one obtains | ||
| + | \[\chi =\pm\eta +const.\]</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 183: | Line 299: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Consider the FLRW metrics in coordinates $(\eta,\chi,\theta,\varphi)$ (\ref{FLRWconformal}). In the case of radial motion $u^{\theta}=u^{\varphi}=0$, so one needs only the components of connection with the indices equal to $\eta$ and $\chi$. They are evaluated using the explicit formula in terms of the metrics (\ref{GammaChristoffel}). The non-zero components are the following: |
| + | \[{\Gamma^{\eta}}_{\eta\eta} | ||
| + | ={\Gamma^{\eta}}_{\chi\chi} | ||
| + | ={\Gamma^{\chi}}_{\eta\chi}=\frac{a'}{a},\] | ||
| + | where the prime denotes the derivative with respect to $\eta$. | ||
| + | |||
| + | Then the equation for geodesic $u^{\mu}(\lambda)$ reduces to | ||
| + | \[\frac{du^{\eta}}{d\lambda} | ||
| + | +{\Gamma^{\eta}}_{\eta\eta}(u^{\eta})^{2} | ||
| + | +{\Gamma^{\eta}}_{\chi\chi}(u^{\chi})^{2}=0; | ||
| + | \qquad | ||
| + | \frac{du^{\chi}}{d\lambda} | ||
| + | +2{\Gamma^{\chi}}_{\eta\chi}u^{\eta}u^{\chi}=0,\] | ||
| + | and after substitution of explicit expressions for the Christoffel symbols one gets | ||
| + | \begin{equation}\label{equGeo1-eq1} | ||
| + | \frac{du^{\eta}}{d\lambda} | ||
| + | +\frac{a'}{a}\Big[(u^{\eta})^{2}+(u^{\chi})^{2}\Big]=0 | ||
| + | ;\qquad | ||
| + | \frac{du^{\chi}}{d\lambda} | ||
| + | +2\frac{a'}{a}u^{\eta}u^{\chi}=0. | ||
| + | \end{equation} | ||
| + | These equations are complemented by the normalization condition for the $4$-velocity: | ||
| + | \begin{equation}\label{equGeo1-eq2} | ||
| + | \epsilon^{2}=u^{\mu}u_{\mu} | ||
| + | =g_{\mu\nu}u^{\mu}u^{\nu} | ||
| + | =g_{\eta\eta}(u^{\eta})^{2} | ||
| + | +g_{\chi\chi}(u^{\chi})^{2} | ||
| + | =a^{2}\big[(u^{\eta})^{2}-(u^{\chi})^{2}\big], | ||
| + | \end{equation} | ||
| + | where $\epsilon^2 =0$ for massless particles (photons) and $\epsilon^2 =1$ for massive ones. | ||
| + | |||
| + | Using equation (\ref{equGeo1-eq2}), one can rewrite the geodesic equations for massive and massless particles (\ref{equGeo1-eq1}) in the form | ||
| + | \[\frac{du^{\eta}}{d\lambda} | ||
| + | +\frac{a'}{a}(u^{\eta})^{2}=\epsilon^{2}\frac{a'}{a^3}; | ||
| + | \qquad | ||
| + | \frac{du^{\chi}}{d\lambda} | ||
| + | +2\frac{a'}{a}u^{\eta}u^{\chi}=0.\] | ||
| + | Taking into account that | ||
| + | \[a' u^{\eta}=\frac{da}{d\eta}\frac{d\eta}{d\lambda} | ||
| + | =\frac{da}{d\lambda},\] | ||
| + | one can present the right hand side in the form of total derivative and reduce them to | ||
| + | \begin{align}\label{equGeo1-eq3} | ||
| + | \frac{d}{d\lambda}\big(a^{2} u^{\eta}\big) | ||
| + | =&+\frac{d}{d\lambda}\big(u_{\eta}\big) | ||
| + | =\epsilon^{2}\mathcal{H} | ||
| + | ;\\ \label{equGeo1-eq4} | ||
| + | \frac{d}{d\lambda}\big(a^{2} u^{\chi}\big) | ||
| + | =&-\frac{d}{d\lambda}\big(u_{\chi}\big)=0. | ||
| + | \end{align} | ||
| + | Here we also took into account that $u_{\eta}=a^{2}u^{\eta}$, $u_{\chi}=-a^{2}u^{\chi}$. | ||
| + | |||
| + | It is easy to see that for photons with $\epsilon^{2}=0$ and $u^{\chi}=\pm u^{\eta}$ the two equations coinside. The particles's momenta, both for massive and massless ones, are always conserved in coordinates $(\eta,\chi)$ (for massive particles $p_{\chi}=mc u_{\chi}$, for photons $k_{\chi}\sim u_{\chi}$). It is as it ought to be, as the FLRW metric is spatially homogeneous. It means that the photon's energy is conserved as well, but in the case of massive particles the Hubble's constant serves as a source of energy. It should be stressed that, though the obtained result is obviously physically meaningful, $u_{\eta}$ and $u_{\chi}$ are not the energy and momentum as measured by a comoving observer. Regarding this see the next problem.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 196: | Line 363: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">The equations for radial geodesics (\ref{equGeo1-eq2}--\ref{equGeo1-eq4}) reduce to the form |
| + | \begin{equation}\label{equGeo2-eq1} | ||
| + | u_{\chi}\equiv\pi_{0}=const;\qquad | ||
| + | (u^{\eta})^{2}=(u^{\chi})^{2}+\epsilon^{2}/a^{2}. | ||
| + | \end{equation} | ||
| + | |||
| + | The physical energy and momentum are those measured by a comoving observer. In coordinates $(\eta,\chi)$ its $4$-velocity is | ||
| + | \[\tilde{u}^{\mu}=\tfrac{1}{a}\delta^{\mu}_{0} | ||
| + | =\tfrac{1}{a}\,(1,0,0,0),\] | ||
| + | where the factor $1/a$ is necessary to satisfy the normalization conditions | ||
| + | \[1=\tilde{u}^{\mu}\tilde{u}_{\mu} | ||
| + | =g_{\eta\eta}(\tilde{u}^{\eta})^{2} | ||
| + | =a^{2}(\tilde{u}^{\eta})^{2}.\] | ||
| + | |||
| + | The photon's frequency measured by this observer equals to (see problem(\ref{equ_oto1a})) | ||
| + | \[\omega_{ph}=k_{\mu}\tilde{u}^{\mu} | ||
| + | =k_{\eta}\tilde{u}^{\eta} | ||
| + | \sim \frac{k_{\chi}}{a}\sim \frac{u_{\chi}}{a} | ||
| + | \sim \frac{1}{a}.\] | ||
| + | |||
| + | From the normalization condition for massive particles it follows that | ||
| + | \[u^{\eta}=\sqrt{(u^{\chi})^2+1/a^2},\] | ||
| + | so the measured energy for a particle of unit mass (here $c=1$) is | ||
| + | \[E_{m}^{(1)}=u^{\mu}\tilde{u}_{\mu} | ||
| + | =g_{\eta\eta}\tilde{u}^{\eta}u^{\eta} | ||
| + | =a^{2}\frac{1}{a}u^{\eta} | ||
| + | =\sqrt{a^{2}(u^\chi)^2+1} | ||
| + | =\sqrt{\frac{\pi_{0}^{2}}{a^2}+1}.\] | ||
| + | Then its physical momentum equals to | ||
| + | \[p_{ph}^{(1)}=\sqrt{E^2 -1}=\frac{\pi_{0}}{a},\] | ||
| + | and for the physical velocity one obtains | ||
| + | \[v_{ph}=\frac{p}{E} | ||
| + | =\frac{\pi_0}{\sqrt{\pi_0^2+a^{2}}}.\]</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 207: | Line 406: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">By definition, the redshift is |
| + | \begin{equation}\label{RedshiftDefinition} | ||
| + | z =\frac{\omega_{emit}-\omega_{obs}} | ||
| + | {\omega_{obs}}, | ||
| + | \end{equation} | ||
| + | and if $\omega\sim 1/a$ then | ||
| + | \begin{equation}\label{Redshift} | ||
| + | 1+z=\frac{\omega_{emit}}{\omega_{obs}} | ||
| + | =\frac{a_{obs}}{a_{emit}}. | ||
| + | \end{equation} | ||
| + | Let at the moment of observation $a_{obs}=1$ and we consider the dependence of redshift $z(t)$ and scale factor $a(t)$ on the time of emission $t$: | ||
| + | \begin{equation}\label{1+z} | ||
| + | 1+z=\frac{1}{a(t)}. | ||
| + | \end{equation} | ||
| + | Then | ||
| + | \[dz=-\frac{da}{a^{2}}=-\frac{H}{a}dt | ||
| + | =-(1+z)Hdt=-H\,dz,\] | ||
| + | and after integration one finds | ||
| + | \[ t = \int\limits_z^\infty \frac{dz}{(1 + z)H(z)}; | ||
| + | \quad | ||
| + | \eta=\int\limits_z^\infty\frac{dz}{H(z)}.\] | ||
| + | The integration constant is chosen so that $z\to\infty$ for $t\to0$. Thus the history of the Universe in the cosmic and conformal times is expressed in terms of redshift.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 218: | Line 438: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">As the comoving distance between the source and observer does not change, the conformal time interval between two light signals at the point of emission coincides with that at the point of detection (see problem (\ref{equ65})). Using the definition of conformal time $dt=a(\eta)d\eta$, one obtains |
| + | \[\left. \frac{\Delta t}{a} \right|_{emit} | ||
| + | = \left. \frac{\Delta t}{a}\right|_{obs}.\] | ||
| + | It follows now that | ||
| + | \[\omega _{obs}a_0 = \omega _{emit}a(t).\] | ||
| + | |||
| + | After substitution into the definition (\ref{RedshiftDefinition}), one has again $a(z) = \frac{1}{{1 + z}}$.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 229: | Line 455: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">No.</p> |
</div> | </div> | ||
</div> | </div> | ||
| Line 240: | Line 466: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">We use explicit expressions for ${\Gamma^{i}}_{kl}$ (\ref{GammaChristoffel}) |
| + | \[\Gamma _{\alpha \beta }^{\mu }= \frac{1}{2}g^{\mu \nu }\left[ | ||
| + | \frac{\partial g_{\alpha \nu }}{\partial x^{\beta }}+\frac{\partial g_{\beta \nu }}{\partial x^{\alpha }}-\frac{\partial g_{\alpha \beta }}{\partial x^{\nu }} \right].\] | ||
| + | Here we use Greek alphabet for spacetime indices $\alpha,\beta,\nu=0,1,2,3$ and Latin for spatial indices $i,j=1,2,3$. | ||
| + | |||
| + | First, we consider the flat case. Then | ||
| + | \[\Gamma _{\alpha \beta }^{0} | ||
| + | =-\frac{1}{2} | ||
| + | \frac{\partial {{g}_{\alpha \beta }}}{\partial t}.\] | ||
| + | |||
| + | The derivatives are non-zero only if $\alpha ,\beta $ are spatial indices $i,j=1,2,3$: | ||
| + | \[\Gamma _{00}^{0}=0,\quad \Gamma _{0i}^{0} | ||
| + | =\Gamma _{i0}^{0}=0,\quad \Gamma _{ij}^{0} | ||
| + | ={{\delta }_{ij}}\dot{a}a.\] | ||
| + | |||
| + | The symbols $\Gamma _{\alpha \beta }^{i}$ are non-zero only if one of the indices is spatial and the other is temporal | ||
| + | \[\Gamma _{0j}^{i}=\Gamma _{j0}^{i} | ||
| + | ={{\delta }_{ij}}\frac{{\dot{a}}}{a}.\] | ||
| + | |||
| + | In the general case we present the FLRW metric in the form | ||
| + | \[d{{s}^{2}}=d{{t}^{2}}-{{a}^{2}}(t) | ||
| + | \gamma_{ij}(x)d{{x}^{i}}d{{x}^{j}},\] | ||
| + | where the non-zero components of the three-dimensional metric $\gamma_{ij}$ are | ||
| + | \[\gamma_{11}= \gamma_{rr} = \frac{1}{1-k r^2},\quad \gamma_{22}=\gamma_{\theta \theta}=r^2;\quad \gamma_{33} = \gamma_{\varphi \varphi } = r^2\sin^2\theta.\] | ||
| + | |||
| + | The non-zero components of the metric tensor ${{g}_{\alpha \beta }}$ and its inverse ${{g}^{\alpha \beta }}$ are the following: | ||
| + | \[ g_{00}= 1,~g_{ij}=- a^2(t)\gamma_{ij}; | ||
| + | \quad g^{00}=1, | ||
| + | \quad g^{ij}=-\frac{1}{a^2(t)}{\gamma^{ij}}.\] | ||
| + | Using again the expression (\ref{GammaChristoffel}), for the non-zero Christoffel symbols we obtain | ||
| + | \[ \Gamma _{0j}^{i} | ||
| + | =\frac{1}{2}g^{ik}\frac{\partial g_{jk}}{\partial t} | ||
| + | = \frac{\dot{a}}{a}\delta_{ij}; | ||
| + | \quad\Gamma _{ij}^0=a\dot{a}{\gamma _{ij}}.\] | ||
| + | The symbols $\Gamma _{jk}^{i}$ are calculated with the help of (\ref{GammaChristoffel}), where instead of the metric tensor $g^{\mu\nu}$ one uses the three-dimensional metric $\gamma_{ij}$. Therefore all the non-zero Christoffel symbols generated by the FLRW-metric are | ||
| + | \begin{align*} | ||
| + | &\Gamma _{11}^{0}=\frac{a\dot{a}}{1-k{{r}^{2}}};\quad | ||
| + | \Gamma _{22}^{0}= a\dot{a}{r^2};\quad | ||
| + | \Gamma _{33}^{0}=a\dot{a}{r^2}\sin^2\theta\\ | ||
| + | &\Gamma_{10}^1=\Gamma _{01}^1 =\frac{\dot a}{a}; | ||
| + | \quad | ||
| + | \Gamma _{11}^1 =-\frac{kr}{1-kr^2};\quad | ||
| + | \Gamma _{22}^1=-r(1-kr^2);\quad | ||
| + | \Gamma _{33}^1=-r(1-kr^2)\sin^2\theta;\\ | ||
| + | &\Gamma^{2}_{20}=\Gamma^{2}_{02} | ||
| + | = \frac{\dot{a}}{a};\quad | ||
| + | \Gamma^{2}_{21}=\Gamma^{2}_{12}=\frac 1 r ;\quad | ||
| + | \Gamma^{2}_{33}=-\sin\theta\cos\theta;\\ | ||
| + | &\Gamma^{3}_{30}=\Gamma^{3}_{03} | ||
| + | =\frac{\dot{a}}{a};\quad | ||
| + | \Gamma^{3}_{31}=\Gamma^{3}_{13}=\frac 1 r ;\quad | ||
| + | \Gamma^{3}_{32}=\Gamma^{3}_{23} | ||
| + | =\coth\theta. | ||
| + | \end{align*}</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 251: | Line 530: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">From (\ref{RiemannTensor}) the components of Ricci tensor are given by |
| + | \[R_{\nu \sigma } | ||
| + | = \Gamma _{\nu \sigma ,\mu }^\mu | ||
| + | - \Gamma _{\nu \mu ,\sigma }^\mu | ||
| + | +\Gamma_{\nu \sigma }^{\alpha} | ||
| + | \Gamma _{\alpha \mu }^\mu | ||
| + | - \Gamma _{\nu \mu }^\alpha | ||
| + | \Gamma _{\alpha \sigma }^{\mu}.\] | ||
| + | Using the Christoffel symbols obtained in the previous problem, one gets | ||
| + | \[\begin{gathered} | ||
| + | R_{00} = - 3\frac{\ddot a}{a}; \hfill\\ | ||
| + | R_{ij} = \left( \ddot aa + 2\dot a^2 + 2k\right) | ||
| + | \gamma _{ij}:\hfill \\ | ||
| + | R_{11} = \frac{\left( {\ddot aa + 2\dot a^2 + 2k} \right)}{1 - kr^2 };\hfill\\ | ||
| + | R_{22} = \left( \ddot aa + 2\dot a^2 + 2k \right)r^2 ; \hfill\\ | ||
| + | R_{33} = \left( \ddot aa + 2\dot a^2 + 2k \right)r^2 \sin ^2 \theta \hfill. | ||
| + | \end{gathered}\] | ||
| + | All other components of the tensor are equal to zero. It is useful also to calculate components of $R_\mu ^\nu$ | ||
| + | \begin{align*} | ||
| + | &R_\mu ^\nu = g^{\nu \alpha } R_{\alpha \mu } ; \\ | ||
| + | &R_0^0 = g^{00} R_{00} = R_{00} | ||
| + | = - 3\frac{{\ddot a}}{a}; \\ | ||
| + | &R_1^1 = R_2^2 = R_3^3 | ||
| + | = - \frac{\ddot aa + 2\dot a^2 + 2k}{a^2}. | ||
| + | \end{align*}</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 262: | Line 565: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Using the results of the previous problem one obtains |
| + | \begin{align*} | ||
| + | & R = g^{\mu \nu } R_{\mu \nu } | ||
| + | = g^{00} R_{00} + g^{ij} R_{ij} | ||
| + | = R_{00} - \frac{1}{a^2}\gamma ^{ij} R_{ij};\\ | ||
| + | &R_{ij} = | ||
| + | \left(\ddot{a}a+2\dot{a}^2+2k\right)\gamma _{ij};\\ | ||
| + | &R = - 6\left( \frac{\ddot a}{a} | ||
| + | + \frac{\dot a^2}{a^2} + \frac{k}{a^2} \right). | ||
| + | \end{align*} | ||
| + | |||
| + | The spatial curvature can be obtained from $R$ by formal substitution $g_{\alpha\beta}\to-g_{\alpha\beta}$ and $a=const$ (thus $R^{0}_{0}$ also turns to zero). The scalar spacetime curvature then equals to $R=-6k/a^2$. If one changes the sign of the metric, then $\Gamma_{ikl}$ changes its sign too, but ${\Gamma^{i}}_{kl}=g^{ij}\Gamma_{j,kl}$ does not, as well as the curvature tensor ${R^{i}}_{klm}$ and Ricci tensor $R_{km}={R^{i}}_{kim}$, but the scalar curvature $R=g^{km}R_{km}$ changes its sign again. Then the spatial curvature equals to ${}^{(3)}R=6k/a^{2}$, and thus $k$ coincides with its sign.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 273: | Line 587: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">In order to obtain the explicit expression for the energy-momentum tensor in a curved spacetime, we consider first the case of flat spacetime. The energy-momentum tensor for isotropic distribution of matter at rest as a whole in the absence of internal rotations is known to have the following form |
| + | \begin{equation} | ||
| + | T^{\mu\nu}= | ||
| + | \left | ||
| + | (\begin{array}{cccc} | ||
| + | \rho & 0& 0& 0\\ | ||
| + | 0 & p& 0& 0\\ | ||
| + | 0 & 0& p& 0\\ | ||
| + | 0 & 0& 0& p\\ | ||
| + | \end{array} | ||
| + | \right) \label{1_equ29n} | ||
| + | \end{equation} | ||
| + | Let us generalize this expression for the case of matter in motion. In the latter case, in addition to dependence on energy density and pressure, the energy-momentum tensor must also depend on the $4$-velocity vector $u^\mu$. In order to obtain this dependence, note that in the comoving frame the $4$-velocity vector equals to | ||
| + | \[u^\mu = (1,0,0,0).\] | ||
| + | Therefore if we define the tensor quantity | ||
| + | \begin{equation} | ||
| + | (\rho+p)u^\mu u^\nu - p\eta^{\mu\nu}, | ||
| + | \label{2_equ29n} | ||
| + | \end{equation} | ||
| + | in the comoving frame it will coincide with the energy-momentum tensor (\ref{2_equ29n}). As both quantities transform as tensors, they coincide in any other frame. | ||
| + | |||
| + | The simplest way to generalize the expression (\ref{1_equ29n}) for the case of curved space is to replace the Minkowski space metric $\eta^{\mu\nu}$ by an arbitrary one $g^{\mu\nu} $. Indeed, for any given point of the spacetime there exists a locally Lorentzian reference frame (see problem (\ref{equ_oto3})), in which the metric tensor locally coincides with the Minkowski tensor, and the energy-momentum tensor for matter takes the form (\ref{2_equ29n}). After transition to arbitrary reference frame one arrives to: | ||
| + | \begin{equation} | ||
| + | T^{\mu\nu}= (\rho+p)u^\mu u^\nu - pg^{\mu\nu} . \label{3_equ29n} | ||
| + | \end{equation} | ||
| + | It is worth noting that in general the expression (\ref{3_equ29n}) is valid only in the case of weak gravity; otherwise the expression for the energy-momentum tensor may contain additional terms depending on the curvature tensor. | ||
| + | |||
| + | Note also that the simplest way to present explicitly the components of energy-momentum tensor (\ref{3_equ29n}) is the following | ||
| + | \begin{equation} | ||
| + | T_\mu ^\nu = g^{\nu \alpha } T_{\alpha \mu } = (\rho+p)u^\nu u_\mu - pg_\mu^\nu = (\rho+p) u^\nu u_\mu - p\delta_\mu^\nu ,\label{4_equ29n} | ||
| + | \end{equation} | ||
| + | and therefore | ||
| + | \begin{equation} | ||
| + | T_\mu ^\nu = | ||
| + | \left | ||
| + | (\begin{array}{cccc} | ||
| + | \rho & 0& 0& 0\\ | ||
| + | 0 & -p& 0& 0\\ | ||
| + | 0 & 0& -p& 0\\ | ||
| + | 0 & 0& 0& -p\\ | ||
| + | \end{array} | ||
| + | \right), | ||
| + | \end{equation} | ||
| + | and so the trace of $T^{\mu}_{\nu}$ is | ||
| + | \[T\equiv T_\mu ^\mu = \rho - 3p.\] | ||
| + | \end{enumerate}</p> | ||
</div> | </div> | ||
</div> | </div> | ||
Revision as of 19:03, 31 May 2012
Contents
- 1 Friedman-Lemaitre-Robertson-Walker (FLRW) metric
- 1.1 Problem 1.
- 1.2 Problem 2.
- 1.3 Problem 3.
- 1.4 Problem 4.
- 1.5 Problem 5.
- 1.6 Problem 6.
- 1.7 Problem 7.
- 1.8 Problem 8.
- 1.9 Problem 9.
- 1.10 Problem 10.
- 1.11 Problem 11.
- 1.12 Problem 12.
- 1.13 Problem 13.
- 1.14 Problem 14.
- 1.15 Problem 15.
- 1.16 Problem 16.
- 1.17 Problem 17.
- 1.18 Problem 18.
- 1.19 Problem 19.
- 1.20 Problem 20.
- 1.21 Problem 21.
- 1.22 Problem 22.
Friedman-Lemaitre-Robertson-Walker (FLRW) metric
Problem 1.
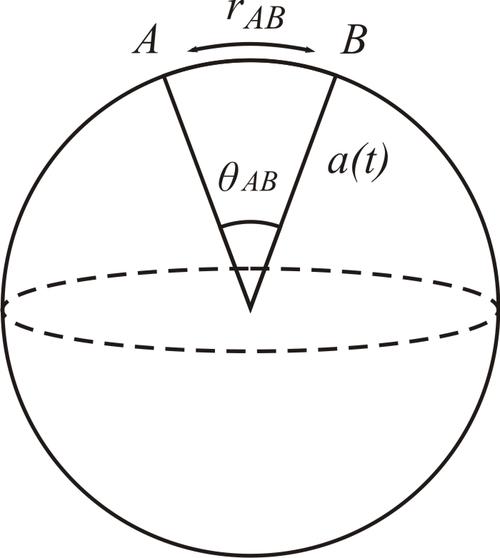
Consider two points $A$ and $B$ on a two-dimensional sphere with radius $a(t)$ depending on time. Find the distance between the points $r_{AB}$, as measured along the surface of the sphere, and their relative velocity $v_{AB}={dr_{AB}}/{dt}$.
When the radius of the sphere grows with time as $a(t)$, the angle $\theta_{AB}$ between two arbitrary points $A$ and $B$ is constant. Therefore the distance between the points changes as \[r_{AB}(t) = a(t)\theta _{AB}\] and relative velocity is \[v_{AB} = \dot r_{AB} = \dot a(t)\theta _{AB} = \frac{\dot a}{a}r_{AB}.\] On denoting \[\frac{\dot a}{a} \equiv H(t),\] one recovers the Hubble's law.
Problem 2.
The comoving reference frame is defined so that matter is at rest in it, and the distance $\chi_{AB}$ between any two points $A$ and $B$ is constant. Show that in a homogeneous and isotropic Universe the proper (physical) distance $r_{AB}$ between two points is related to the comoving one as \[r_{AB}=a(t)\cdot \chi_{AB},\] where quantity $a$ is called the scale factor and it can depend on time only. Integrate the Hubble's law and find $a(t)$.
Suppose $a=a(r,t)$. Then we differentiate $r_{AB}$ with respect to time to obtain \[V_{AB}=\chi_{AB}\; \dot{a} =r_{AB}\frac{\dot{a}}{a},\] so it is easy to see that \[H=\frac{\dot{a}}{a},\] where the scale factor $a(r,t)$ can be expressed in terms of the Hubble's parameter as \[a(t) = a_{0}\exp \left( \int H(t)dt \right),\] and thus it can depend solely on time. The scale factor represents an analogue of radius of the two-dimensional sphere from the previous problem. Its normalization is arbitrary and it determines the unit of length in the comoving reference frame. If the normalization is fixed then the scale factor determines distance between objects or observers at a given moment of time. The comoving distance between them $\chi_{AB}$ is analogous to the angle $\theta_{AB}$ from the previous problem and it can be treated as a Lagrangian (comoving) coordinate of the point $B$ in the reference frame centered in point $A$.
Problem 3.
Consider a spacetime with homogeneous and isotropic spatial section of constant time $dt=0$. Show that in the comoving coordinates its metric necessarily has the form of the Friedman-Lemaitre-Robertson-Walker (FLRW)$^*$ metric: \begin{equation}\label{FLRW1} ds^2=dt^2-a^2(t) \left\{ d\chi^2+\Sigma^2(\chi) (d\theta^2+\sin^2\theta d\varphi^2)\right\}, \end{equation} where \[\Sigma^2(\chi)= \left\{\begin{array}{lcl} \sin^2\chi \\%\qquad \; \; k=+1\\ \chi^2 \\%\qquad \qquad k=0\\ \sinh^2 \chi. \\%\qquad k=-1,\\ \end{array}\right.\] The time coordinate $t$, which is the proper time for the comoving matter, is referred to as cosmic (or cosmological) time.
$^*$Depending on geographical or historical preferences, named after a subset of the four scientists: Alexander Friedmann, Georges Lemaitre, Howard Percy Robertson and Arthur Geoffrey Walker. Thus abbreviations FRW, RW or FL are also used.
IMAGE!!! Spatial isotropy implies spherical symmetry. In this case the spatial line element in comoving coordinates $(\chi,\vartheta,\phi)$ takes the form: \[dl ^2 = d\chi^2 + f^2 (\chi) \left( d\vartheta ^2 + \sin^2\vartheta d\phi ^2 \right),\] where $f(\chi)$ is a real-valued function which must satisfy the condition $f(\chi)\approx \chi $ at $\chi \rightarrow 0$ in the case of non-singular metrics. Let us fix the angle $\theta$ and consider the triangle $DGE$ in the plane $\theta=\pi/2$, shown on Fig.~\ref{fig:G}. Here $DH=HE=\chi$, $HA=\delta$, the distance $DE$ and angle $\gamma$ are assumed to be small. Angles $GDH$ and $GEH$ are both equal to $\gamma$ due to homogeneity and isotropy. Note also that \begin{equation}\label{21-1} EF \simeq EF' = f( 2\chi )\gamma = f( \chi)\beta \end{equation} and \begin{equation}\label{21-2} AC = \gamma f(\chi+\delta) = AB + BC =\gamma f(\chi-\delta) + \beta f(\delta). \end{equation} Using (\ref{21-1}), we exclude the ratio $\beta /\gamma $ from (\ref{21-2}) and in the limit $\delta \to 0$ obtain the equation \begin{equation}\label{21-3} \frac{df}{d\chi} =\frac{f( 2\chi)}{2f(\chi)}\cdot \frac{df}{d\chi}\Big|_{\chi=0}. \end{equation} We are interested in its solutions which satisfy $df(\chi)/d\chi\big|_{\chi=0}=1$. It is easy to verify that functions $\chi$, $\sin\chi$ and $\sinh\chi$ are all such solutions. We note also, that if $f(\chi)$ is a solution of the equation (\ref{21-3}), then $f(\chi/\alpha)$, where $\alpha$ is an arbitrary constant, is also a solution. If we assume that $f$ is analytic and expand it into series over $\chi$, it is easy to show that up to rescaling $\chi\to \chi/\alpha$ all the possible solutions of (\ref{21-3}) are given by the following three: \[f(\chi)=\Sigma(\chi)=\left\{\begin{array}{l} \sin \chi\\ \chi\\ \sinh \chi\;. \end{array}\right.\] Without violation of homogeneity and isotropy, the line element of the three-dimensional space can be multiplied by an arbitrary function of time, and thus the general form of the spacetime metric is \[ds^2=dt^2-a^2(t) \left\{ d\chi^2+f^2(\chi) (d\theta^2+\sin^2\theta d\varphi^2)\right\}.\]
Problem 4.
Show that the FLRW metric (\ref{FLRW1}) can be presented in the form \begin{equation}\label{FLRW2} ds^2=dt^2-a^2(t) \left\{ \frac{dr^2}{1-kr^2}+r^2 (d\theta^2+\sin^2\theta d\varphi^2) \right\}, \end{equation} where $k=0,\pm1$ is the sign of spatial curvature (see problem).
In each of the three cases we introduce a new variable \[r\equiv \Sigma(\chi)=\left\{\begin{array}{lcl} \sin\chi \\%\qquad \; \; k=+1\\ \chi \\%\qquad \qquad k=0\\ \sinh\chi \\%\qquad k=-1\\ \end{array}\right.,\qquad dr=\left\{\begin{array}{lcl} \cos\chi d\chi\\ d\chi\qquad\\ \cosh\chi d\chi\\ \end{array},\right.\] so that \[ d\chi^2 =\frac{dr^2}{1-kr^2}, \quad\text{where}\quad k=\left\{\begin{array}{rcl} +1&\quad\text{if}\quad& r=\sin\chi \\ 0&\quad\text{if}\quad& r=\chi\\ -1&\quad\text{if}\quad& r=\sinh\chi \end{array}\right.\] and finally obtain \[ ds^2=dt^2-a^2(t) \left\{ \frac{dr^2}{1-kr^2}+r^2 (d\theta^2+\sin^2\theta d\varphi^2) \right\}.\]
Problem 5.
Show that only the sign of spatial curvature has physical meaning, as renormalization of the scale factor rescales the curvature.
Suppose we have metric \[ ds^2=dt^2-\alpha^2(t) \Big\{ \frac{dr^2}{1-k \beta^{2}r^2}+r^2 (d\theta^2+\sin^2\theta d\varphi^2) \Big\},\] where $\beta=const$. Then we can always introduce $\chi=\beta r$ and $a(t)=\alpha(t)/\beta$ and bring the metric to the canonical form (\ref{FLRW2}). Note, that this has sense only if $k\neq 0$.
Problem 6.
Why is the normalization of the scale factor not fixed for a spatially flat Universe, for which $k=0$?
It follows from the fact that in the case of a flat Universe there is no spatial scale to normalize the scale factor by.
Problem 7.
Consider a closed Universe (with $k=+1$) and find the length of equator and full volume of its spatial section $dt=0$.
In the case of closed Universe the spatial line element takes the form \[dl^2=a^2(t)\left\{d\chi^2 +\sin^{2}\chi(d\theta^2+\sin^2\theta d\phi^2)\right\}.\] Then the area of a sphere with radius $\chi$, circumscribed around the center, equals to \[s(\chi)= 4\pi a^2(t) \sin^2(\chi),\] and the equator's length is \[l=2\pi a(t) \sin(\chi).\] It can be seen from the relation for $s(\chi)$ that $s$ reaches maximum $s_{max} = 4\pi a^2(t)$ at $\chi=\pi/2$, then decreases and turns again to zero at $\chi = \pi$. Thus the value $\chi = \pi$ gives the maximum value the coordinate $\chi$ can take. The volume inside a sphere of radius $\chi$ equals to \[V =\int\limits_0^{\chi} s(\chi') a(t) d\chi' = 4\pi a^3(t) \int\limits_0^{\chi} \sin^2(\chi') d\chi' = 4\pi a^3(t)\left(\frac 1 2 \chi - \frac 1 4 \sin(2\chi) \right)\] and monotonically grows with $\chi$. At $\chi = \pi$ one obtains the total volume of the closed world: \[V_{universe} = 2 \pi^2 a^3.\]
Problem 8.
Present arguments in favor of the affirmation that the electric charge of a closed Universe should be exactly zero.
A charge is a source of electric field. In Euclidean space the electric field lines begin on a charge and then either end on a charge of the opposite sign or go to infinity. However there is no infinity in the closed world. Let us fix some arbitrary electric field distribution $\vec E$ in the closed world and find the corresponding charge density $\varepsilon _e$ using the equation $ \mbox{div}\vec E = 4\pi \varepsilon _e$. It will always turn out that the total charge equals to zero, i.e. $Z = \int \varepsilon_e dV = 0$, as in the absence of infinity the lines of force always start from one charge and necessarily end on another charge of the opposite sign, which thus neutralizes the former charge.
Problem 9.
Using the FLRW metric, derive the Hubble's law.
In an expanding Universe the physical distance $D$ between the observer in the origin of reference frame and a receding galaxy is measured along the surface of constant time $dt=0$. If one considers the radial distance then $d\theta=d\phi=0$, so \[D(t) = a(t)\chi.\] Evaluating time derivative and taking into account that $\dot \chi = 0,$ one obtains \[ V \equiv \frac{dD(t)}{dt} = \dot a(t)\chi = \frac{\dot a(t)}{a(t)}a(t)\chi = H(t)D.\]
Problem 10.
Conformal time $\eta$ is defined as \[dt=a(\eta)d\eta.\] It can be interpreted as the time measured by a clock that decelerates along with the expansion of the Universe. Rewrite the FLRW metric in conformal time. Show that the logarithmic derivative of the scale factor with respect to conformal time determines its evolution in the physical time.
On substitution $dt=a d\eta$ we get \begin{equation}\label{FLRWconformal} d{s^2} = a^2(\eta ) \Big\{ d\eta ^2 - \big[ d\chi ^2 + \Sigma ^2(\chi )\left( d\theta ^2 + \sin^2\theta\; d\varphi ^2\right)\big]\Big\}. \end{equation} Then \[\dot{a}=\frac{da}{dt}=\frac{da}{ad\eta} =\frac{d\,\ln a}{d\eta}.\]
Problem 11.
Express the FLRW metric in comoving coordinates and conformal time. Show that in the case $k=0$ it is conformally flat, i.e. it can be made flat (pseudo-Euclidean) by means of global stretching.
In comoving coordinates the FLRW metric has the form \[d{s^2} = d{t^2} - a^2(t)\delta _{ij}dx^{i}dx^{j},\] then the change of variables $dt=a(\eta)d\eta$ leads to metric \[ds^2 = a^2(\eta ) \left[ d\eta ^2 - \delta _{ij}dx^idx^j \right],\] and it follows that $g_{\mu \nu } = a^2(\eta )\eta _{\mu \nu }$, where $\eta _{\mu \nu }$ is the Minkowski metric.
Problem 12.
Consider an arbitrary function of time $f(t)$ and express $\dot{f}$ and $\ddot{f}$ in terms of derivatives with respect to conformal time.
Let us denote differentiation with respect to time $t$ by a dot, and with respect to conformal time $\eta$ by a prime. Then \begin{align*} &\dot f = \frac{f'}{a};\\ &\ddot f=\frac{f''}{a^2} - \frac{f'a'}{a^3} = \frac{f''-\mathcal{H} f'}{a^2}, \quad\text{where}\quad \mathcal{H}\equiv \frac{a'}{a} \end{align*} is the Hubble' constant in conformal time.
Problem 13.
Obtain the equation of a photon's worldline in terms of conformal time for the case of the isotropic and spatially flat Universe.
A worldline of a photon is defined by equation $d{s^2} =0$. It is sufficient to consider only radial trajectories with the observer in the origin of coordinate frame. Using the metrics (\ref{FLRWconformal}), IT one obtains \[\chi =\pm\eta +const.\]
Problem 14.
Derive the equations of geodesics in terms of conformal time and comoving coordinates for the case of radial motion in the FLRW metric.
Consider the FLRW metrics in coordinates $(\eta,\chi,\theta,\varphi)$ (\ref{FLRWconformal}). In the case of radial motion $u^{\theta}=u^{\varphi}=0$, so one needs only the components of connection with the indices equal to $\eta$ and $\chi$. They are evaluated using the explicit formula in terms of the metrics (\ref{GammaChristoffel}). The non-zero components are the following: \[{\Gamma^{\eta}}_{\eta\eta} ={\Gamma^{\eta}}_{\chi\chi} ={\Gamma^{\chi}}_{\eta\chi}=\frac{a'}{a},\] where the prime denotes the derivative with respect to $\eta$. Then the equation for geodesic $u^{\mu}(\lambda)$ reduces to \[\frac{du^{\eta}}{d\lambda} +{\Gamma^{\eta}}_{\eta\eta}(u^{\eta})^{2} +{\Gamma^{\eta}}_{\chi\chi}(u^{\chi})^{2}=0; \qquad \frac{du^{\chi}}{d\lambda} +2{\Gamma^{\chi}}_{\eta\chi}u^{\eta}u^{\chi}=0,\] and after substitution of explicit expressions for the Christoffel symbols one gets \begin{equation}\label{equGeo1-eq1} \frac{du^{\eta}}{d\lambda} +\frac{a'}{a}\Big[(u^{\eta})^{2}+(u^{\chi})^{2}\Big]=0 ;\qquad \frac{du^{\chi}}{d\lambda} +2\frac{a'}{a}u^{\eta}u^{\chi}=0. \end{equation} These equations are complemented by the normalization condition for the $4$-velocity: \begin{equation}\label{equGeo1-eq2} \epsilon^{2}=u^{\mu}u_{\mu} =g_{\mu\nu}u^{\mu}u^{\nu} =g_{\eta\eta}(u^{\eta})^{2} +g_{\chi\chi}(u^{\chi})^{2} =a^{2}\big[(u^{\eta})^{2}-(u^{\chi})^{2}\big], \end{equation} where $\epsilon^2 =0$ for massless particles (photons) and $\epsilon^2 =1$ for massive ones. Using equation (\ref{equGeo1-eq2}), one can rewrite the geodesic equations for massive and massless particles (\ref{equGeo1-eq1}) in the form \[\frac{du^{\eta}}{d\lambda} +\frac{a'}{a}(u^{\eta})^{2}=\epsilon^{2}\frac{a'}{a^3}; \qquad \frac{du^{\chi}}{d\lambda} +2\frac{a'}{a}u^{\eta}u^{\chi}=0.\] Taking into account that \[a' u^{\eta}=\frac{da}{d\eta}\frac{d\eta}{d\lambda} =\frac{da}{d\lambda},\] one can present the right hand side in the form of total derivative and reduce them to \begin{align}\label{equGeo1-eq3} \frac{d}{d\lambda}\big(a^{2} u^{\eta}\big) =&+\frac{d}{d\lambda}\big(u_{\eta}\big) =\epsilon^{2}\mathcal{H} ;\\ \label{equGeo1-eq4} \frac{d}{d\lambda}\big(a^{2} u^{\chi}\big) =&-\frac{d}{d\lambda}\big(u_{\chi}\big)=0. \end{align} Here we also took into account that $u_{\eta}=a^{2}u^{\eta}$, $u_{\chi}=-a^{2}u^{\chi}$. It is easy to see that for photons with $\epsilon^{2}=0$ and $u^{\chi}=\pm u^{\eta}$ the two equations coinside. The particles's momenta, both for massive and massless ones, are always conserved in coordinates $(\eta,\chi)$ (for massive particles $p_{\chi}=mc u_{\chi}$, for photons $k_{\chi}\sim u_{\chi}$). It is as it ought to be, as the FLRW metric is spatially homogeneous. It means that the photon's energy is conserved as well, but in the case of massive particles the Hubble's constant serves as a source of energy. It should be stressed that, though the obtained result is obviously physically meaningful, $u_{\eta}$ and $u_{\chi}$ are not the energy and momentum as measured by a comoving observer. Regarding this see the next problem.
Problem 15.
A comoving observer is the one that is at rest in the comoving coordinates. He sees the Universe as isotropic, and can also be called an isotropic observer. Show that the frequency of a photon and velocity of a free particle, as measured by a comoving observer$^*$ at time $t$, are proportional to $1/a(t)$.
$^*$We will refer to these quantities as to the "physical" energy and momentum of a particle, to stress that they are the ones directly measured in the most natural way.
The equations for radial geodesics (\ref{equGeo1-eq2}--\ref{equGeo1-eq4}) reduce to the form \begin{equation}\label{equGeo2-eq1} u_{\chi}\equiv\pi_{0}=const;\qquad (u^{\eta})^{2}=(u^{\chi})^{2}+\epsilon^{2}/a^{2}. \end{equation} The physical energy and momentum are those measured by a comoving observer. In coordinates $(\eta,\chi)$ its $4$-velocity is \[\tilde{u}^{\mu}=\tfrac{1}{a}\delta^{\mu}_{0} =\tfrac{1}{a}\,(1,0,0,0),\] where the factor $1/a$ is necessary to satisfy the normalization conditions \[1=\tilde{u}^{\mu}\tilde{u}_{\mu} =g_{\eta\eta}(\tilde{u}^{\eta})^{2} =a^{2}(\tilde{u}^{\eta})^{2}.\] The photon's frequency measured by this observer equals to (see problem(\ref{equ_oto1a})) \[\omega_{ph}=k_{\mu}\tilde{u}^{\mu} =k_{\eta}\tilde{u}^{\eta} \sim \frac{k_{\chi}}{a}\sim \frac{u_{\chi}}{a} \sim \frac{1}{a}.\] From the normalization condition for massive particles it follows that \[u^{\eta}=\sqrt{(u^{\chi})^2+1/a^2},\] so the measured energy for a particle of unit mass (here $c=1$) is \[E_{m}^{(1)}=u^{\mu}\tilde{u}_{\mu} =g_{\eta\eta}\tilde{u}^{\eta}u^{\eta} =a^{2}\frac{1}{a}u^{\eta} =\sqrt{a^{2}(u^\chi)^2+1} =\sqrt{\frac{\pi_{0}^{2}}{a^2}+1}.\] Then its physical momentum equals to \[p_{ph}^{(1)}=\sqrt{E^2 -1}=\frac{\pi_{0}}{a},\] and for the physical velocity one obtains \[v_{ph}=\frac{p}{E} =\frac{\pi_0}{\sqrt{\pi_0^2+a^{2}}}.\]
Problem 16.
Express the detected redshift of a photon as a function of the cosmic time $t$ at the moment of its emission and vice versa: express the time $t$ and conformal time $\eta$ at the moment of its emission in terms of its registered redshift.
By definition, the redshift is \begin{equation}\label{RedshiftDefinition} z =\frac{\omega_{emit}-\omega_{obs}} {\omega_{obs}}, \end{equation} and if $\omega\sim 1/a$ then \begin{equation}\label{Redshift} 1+z=\frac{\omega_{emit}}{\omega_{obs}} =\frac{a_{obs}}{a_{emit}}. \end{equation} Let at the moment of observation $a_{obs}=1$ and we consider the dependence of redshift $z(t)$ and scale factor $a(t)$ on the time of emission $t$: \begin{equation}\label{1+z} 1+z=\frac{1}{a(t)}. \end{equation} Then \[dz=-\frac{da}{a^{2}}=-\frac{H}{a}dt =-(1+z)Hdt=-H\,dz,\] and after integration one finds \[ t = \int\limits_z^\infty \frac{dz}{(1 + z)H(z)}; \quad \eta=\int\limits_z^\infty\frac{dz}{H(z)}.\] The integration constant is chosen so that $z\to\infty$ for $t\to0$. Thus the history of the Universe in the cosmic and conformal times is expressed in terms of redshift.
Problem 17.
Obtain the relation between the scale factor and conformal time using the properties of conformal time interval.
As the comoving distance between the source and observer does not change, the conformal time interval between two light signals at the point of emission coincides with that at the point of detection (see problem (\ref{equ65})). Using the definition of conformal time $dt=a(\eta)d\eta$, one obtains \[\left. \frac{\Delta t}{a} \right|_{emit} = \left. \frac{\Delta t}{a}\right|_{obs}.\] It follows now that \[\omega _{obs}a_0 = \omega _{emit}a(t).\] After substitution into the definition (\ref{RedshiftDefinition}), one has again $a(z) = \frac{1}[[:Template:1 + z]]$.
Problem 18.
Is it possible for an open Universe to evolve into a closed one or vice versa?
No.
Problem 19.
Calculate all connection coefficients (Christoffel symbols) for the FLRW metric.
We use explicit expressions for ${\Gamma^{i}}_{kl}$ (\ref{GammaChristoffel}) \[\Gamma _{\alpha \beta }^{\mu }= \frac{1}{2}g^{\mu \nu }\left[ \frac{\partial g_{\alpha \nu }}{\partial x^{\beta }}+\frac{\partial g_{\beta \nu }}{\partial x^{\alpha }}-\frac{\partial g_{\alpha \beta }}{\partial x^{\nu }} \right].\] Here we use Greek alphabet for spacetime indices $\alpha,\beta,\nu=0,1,2,3$ and Latin for spatial indices $i,j=1,2,3$. First, we consider the flat case. Then \[\Gamma _{\alpha \beta }^{0} =-\frac{1}{2} \frac{\partial {{g}_{\alpha \beta }}}{\partial t}.\] The derivatives are non-zero only if $\alpha ,\beta $ are spatial indices $i,j=1,2,3$: \[\Gamma _{00}^{0}=0,\quad \Gamma _{0i}^{0} =\Gamma _{i0}^{0}=0,\quad \Gamma _{ij}^{0} ={{\delta }_{ij}}\dot{a}a.\] The symbols $\Gamma _{\alpha \beta }^{i}$ are non-zero only if one of the indices is spatial and the other is temporal \[\Gamma _{0j}^{i}=\Gamma _{j0}^{i} ={{\delta }_{ij}}\frac{{\dot{a}}}{a}.\] In the general case we present the FLRW metric in the form \[d{{s}^{2}}=d{{t}^{2}}-{{a}^{2}}(t) \gamma_{ij}(x)d{{x}^{i}}d{{x}^{j}},\] where the non-zero components of the three-dimensional metric $\gamma_{ij}$ are \[\gamma_{11}= \gamma_{rr} = \frac{1}{1-k r^2},\quad \gamma_{22}=\gamma_{\theta \theta}=r^2;\quad \gamma_{33} = \gamma_{\varphi \varphi } = r^2\sin^2\theta.\] The non-zero components of the metric tensor ${{g}_{\alpha \beta }}$ and its inverse ${{g}^{\alpha \beta }}$ are the following: \[ g_{00}= 1,~g_{ij}=- a^2(t)\gamma_{ij}; \quad g^{00}=1, \quad g^{ij}=-\frac{1}{a^2(t)}{\gamma^{ij}}.\] Using again the expression (\ref{GammaChristoffel}), for the non-zero Christoffel symbols we obtain \[ \Gamma _{0j}^{i} =\frac{1}{2}g^{ik}\frac{\partial g_{jk}}{\partial t} = \frac{\dot{a}}{a}\delta_{ij}; \quad\Gamma _{ij}^0=a\dot{a}{\gamma _{ij}}.\] The symbols $\Gamma _{jk}^{i}$ are calculated with the help of (\ref{GammaChristoffel}), where instead of the metric tensor $g^{\mu\nu}$ one uses the three-dimensional metric $\gamma_{ij}$. Therefore all the non-zero Christoffel symbols generated by the FLRW-metric are \begin{align*} &\Gamma _{11}^{0}=\frac{a\dot{a}}{1-k{{r}^{2}}};\quad \Gamma _{22}^{0}= a\dot{a}{r^2};\quad \Gamma _{33}^{0}=a\dot{a}{r^2}\sin^2\theta\\ &\Gamma_{10}^1=\Gamma _{01}^1 =\frac{\dot a}{a}; \quad \Gamma _{11}^1 =-\frac{kr}{1-kr^2};\quad \Gamma _{22}^1=-r(1-kr^2);\quad \Gamma _{33}^1=-r(1-kr^2)\sin^2\theta;\\ &\Gamma^{2}_{20}=\Gamma^{2}_{02} = \frac{\dot{a}}{a};\quad \Gamma^{2}_{21}=\Gamma^{2}_{12}=\frac 1 r ;\quad \Gamma^{2}_{33}=-\sin\theta\cos\theta;\\ &\Gamma^{3}_{30}=\Gamma^{3}_{03} =\frac{\dot{a}}{a};\quad \Gamma^{3}_{31}=\Gamma^{3}_{13}=\frac 1 r ;\quad \Gamma^{3}_{32}=\Gamma^{3}_{23} =\coth\theta. \end{align*}
Problem 20.
Derive the components of Ricci tensor, scalar curvature and the trace of energy-momentum tensor for the FLRW metric.
From (\ref{RiemannTensor}) the components of Ricci tensor are given by \[R_{\nu \sigma } = \Gamma _{\nu \sigma ,\mu }^\mu - \Gamma _{\nu \mu ,\sigma }^\mu +\Gamma_{\nu \sigma }^{\alpha} \Gamma _{\alpha \mu }^\mu - \Gamma _{\nu \mu }^\alpha \Gamma _{\alpha \sigma }^{\mu}.\] Using the Christoffel symbols obtained in the previous problem, one gets \[\begin{gathered} R_{00} = - 3\frac{\ddot a}{a}; \hfill\\ R_{ij} = \left( \ddot aa + 2\dot a^2 + 2k\right) \gamma _{ij}:\hfill \\ R_{11} = \frac{\left( {\ddot aa + 2\dot a^2 + 2k} \right)}{1 - kr^2 };\hfill\\ R_{22} = \left( \ddot aa + 2\dot a^2 + 2k \right)r^2 ; \hfill\\ R_{33} = \left( \ddot aa + 2\dot a^2 + 2k \right)r^2 \sin ^2 \theta \hfill. \end{gathered}\] All other components of the tensor are equal to zero. It is useful also to calculate components of $R_\mu ^\nu$ \begin{align*} &R_\mu ^\nu = g^{\nu \alpha } R_{\alpha \mu } ; \\ &R_0^0 = g^{00} R_{00} = R_{00} = - 3\frac[[:Template:\ddot a]]{a}; \\ &R_1^1 = R_2^2 = R_3^3 = - \frac{\ddot aa + 2\dot a^2 + 2k}{a^2}. \end{align*}
Problem 21.
Obtain the components of the Ricci tensor and scalar curvature ${}^{(3)}R$ of the spatial section $t=const$ of the FLRW metric. Show that $k=sign^{(3)}R$ if ${}^{(3)}R\neq 0$.
Using the results of the previous problem one obtains \begin{align*} & R = g^{\mu \nu } R_{\mu \nu } = g^{00} R_{00} + g^{ij} R_{ij} = R_{00} - \frac{1}{a^2}\gamma ^{ij} R_{ij};\\ &R_{ij} = \left(\ddot{a}a+2\dot{a}^2+2k\right)\gamma _{ij};\\ &R = - 6\left( \frac{\ddot a}{a} + \frac{\dot a^2}{a^2} + \frac{k}{a^2} \right). \end{align*} The spatial curvature can be obtained from $R$ by formal substitution $g_{\alpha\beta}\to-g_{\alpha\beta}$ and $a=const$ (thus $R^{0}_{0}$ also turns to zero). The scalar spacetime curvature then equals to $R=-6k/a^2$. If one changes the sign of the metric, then $\Gamma_{ikl}$ changes its sign too, but ${\Gamma^{i}}_{kl}=g^{ij}\Gamma_{j,kl}$ does not, as well as the curvature tensor ${R^{i}}_{klm}$ and Ricci tensor $R_{km}={R^{i}}_{kim}$, but the scalar curvature $R=g^{km}R_{km}$ changes its sign again. Then the spatial curvature equals to ${}^{(3)}R=6k/a^{2}$, and thus $k$ coincides with its sign.
Problem 22.
Derive the components and trace of the energy-momentum tensor which satisfies the cosmological principle.
In order to obtain the explicit expression for the energy-momentum tensor in a curved spacetime, we consider first the case of flat spacetime. The energy-momentum tensor for isotropic distribution of matter at rest as a whole in the absence of internal rotations is known to have the following form \begin{equation} T^{\mu\nu}= \left (\begin{array}{cccc} \rho & 0& 0& 0\\ 0 & p& 0& 0\\ 0 & 0& p& 0\\ 0 & 0& 0& p\\ \end{array} \right) \label{1_equ29n} \end{equation} Let us generalize this expression for the case of matter in motion. In the latter case, in addition to dependence on energy density and pressure, the energy-momentum tensor must also depend on the $4$-velocity vector $u^\mu$. In order to obtain this dependence, note that in the comoving frame the $4$-velocity vector equals to \[u^\mu = (1,0,0,0).\] Therefore if we define the tensor quantity \begin{equation} (\rho+p)u^\mu u^\nu - p\eta^{\mu\nu}, \label{2_equ29n} \end{equation} in the comoving frame it will coincide with the energy-momentum tensor (\ref{2_equ29n}). As both quantities transform as tensors, they coincide in any other frame. The simplest way to generalize the expression (\ref{1_equ29n}) for the case of curved space is to replace the Minkowski space metric $\eta^{\mu\nu}$ by an arbitrary one $g^{\mu\nu} $. Indeed, for any given point of the spacetime there exists a locally Lorentzian reference frame (see problem (\ref{equ_oto3})), in which the metric tensor locally coincides with the Minkowski tensor, and the energy-momentum tensor for matter takes the form (\ref{2_equ29n}). After transition to arbitrary reference frame one arrives to: \begin{equation} T^{\mu\nu}= (\rho+p)u^\mu u^\nu - pg^{\mu\nu} . \label{3_equ29n} \end{equation} It is worth noting that in general the expression (\ref{3_equ29n}) is valid only in the case of weak gravity; otherwise the expression for the energy-momentum tensor may contain additional terms depending on the curvature tensor. Note also that the simplest way to present explicitly the components of energy-momentum tensor (\ref{3_equ29n}) is the following \begin{equation} T_\mu ^\nu = g^{\nu \alpha } T_{\alpha \mu } = (\rho+p)u^\nu u_\mu - pg_\mu^\nu = (\rho+p) u^\nu u_\mu - p\delta_\mu^\nu ,\label{4_equ29n} \end{equation} and therefore \begin{equation} T_\mu ^\nu = \left (\begin{array}{cccc} \rho & 0& 0& 0\\ 0 & -p& 0& 0\\ 0 & 0& -p& 0\\ 0 & 0& 0& -p\\ \end{array} \right), \end{equation} and so the trace of $T^{\mu}_{\nu}$ is \[T\equiv T_\mu ^\mu = \rho - 3p.\] \end{enumerate}