Influence of cosmological expansion on local systems
Does the expansion of space mean that everything in it is stretched? Galaxies? Atoms? A shallow answer to this question is: "bounded" systems do not take part in the expansion. However, if space is stretched, then how can these systems not experience some, at least minimal, extension? Should bounded systems be stretched less intensively? The following several problems attempt to clarify the question by the example of a simple model: a classical atom, which consists of a negatively charged electron with negligible mass, rotating around a positively charged massive nucleus.
Let us place this atom in a homogeneous Universe which expands with scale factor $a(t)$. We will use two sets of spatial coordinates for its description, both spherical with the atom at the origin. The first set consists of physical coordinates $R,\theta,\varphi$, with $R$ being the distance between the electron and the nucleus at given time. The second set $r,\theta,\varphi$ is the comoving coordinates, the fixed points that partake in the cosmological expansion. The two sets are related through \[R = a(t)r.\] The angular coordinates are the same, as we assume that the cosmological expansion is radial.
Problem 1.
How can we understand in terms of the physical and comoving coordinates whether the atom partakes in the cosmological (Hubble) expansion or not?
If $R=const$, it means there is no expansion. If $r=const$, it means the atom is copmletely "involved" into the cosmological expansion (they say, joins the Hubble flow). Simultaneous alteration of both coordinates corresponds to an intermediate situation. The question whether the intermediate situation can be realized should be considered separately.
Problem 2.
Derive the equation of motion for the atom's electron accounting for the cosmological expansion.
Our model includes a fixed nucleus at the origin of the spherical coordinate frame $R,\theta,\varphi$. The position of the electron of mass $m$ in the equatorial plane $\theta= \pi /2$ is given by functions $R(t),\varphi (t)$. As there are only radial forces, its angular momentum $L =m{R^2}\dot \varphi $ is conserved, and for an electron of unit mass the integral of motion is \[L \equiv {R^2}\dot \varphi.\] In the absence of cosmological expansion the equation of motion for $R(t)$ is well-known \[\ddot R - \frac{L^2}{R^3} = - \frac{C}{R^2},\] where $C$ is the constant of electrostatic interaction. Now we have to take into account the effect of expansion. According to $R = a(t)r$, if a point takes part in the cosmological expansion only, i.e has constant comoving coordinates $r,\theta,\varphi$, its radial acceleration is \[\left. {\ddot R} \right|_{expansion} = R\frac{\ddot a}{a}.\] We can treat this terms as a radial force acting on a unit mass and add it to the equation of motion, leading to \[\ddot R = \frac{L^2}{R^3} - \frac{C}{R^2} + R\frac{\ddot a}{a}.\] The solution of this equation $R\big(r(t)\big)$ for some given $a(t)$ allows us to find the radial coordinate of the electron at the given time. Using the integral of motion $L\equiv {R^2}\dot \varphi$, we can find the angular coordinate $\varphi (t)$. Thus we can obtain full description of the orbit both in physical $R,\theta ,\varphi$ and in the comoving $r,\theta ,\varphi$ frames.
Problem 3.
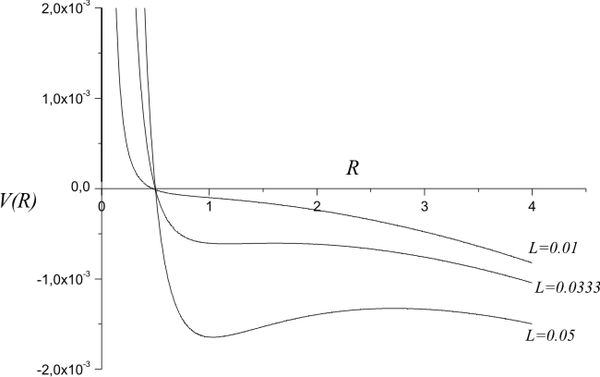
Write the effective potential for the electron for the case of exponential expansion $a(t) = e^{\beta t}$ and use it to analyze the dynamics for the case $L^2=C$, where $C$ is the constant of electrostatic interaction.
In this case \[\ddot R = {L^2}\left( \frac{1}{R^3} - \frac{1}{R^2} \right) + \beta ^2R,\] therefore \[V(R) = \frac{L^2}{2R^2} - \frac{C}{R} - \frac{1}{2}\beta ^2R^2.\]
Problem 4.
Why does the Solar system not expand despite of expansion of all the Universe? Give quantitative arguments.
Restricting ourselves to circular orbits, we write the equation of motion as \[ \frac{d^2\vec r}{dt^2} - \frac{\ddot a}{a}\vec r = - \frac{GM}{r^2}{\vec e}_r;\] On substitution of $r(t) = r_0 + \delta r(t)$ and $\theta (t) = \omega _0t + \delta \theta (t)$, we arrive to \[ r_0\delta \ddot \theta + 2\delta \dot r\omega _0 = 0;\] \[\delta \ddot r - 3\omega _0^2\delta r - 2\omega _0r_0\delta \dot \theta - \frac{\ddot a}{a}r_0 = 0.\] For a Universe dominated by matter $\left(\ddot a/a = - 2/9t^2 \right)$ so the term $\delta \ddot r$ is negligible and \[r(t) \simeq r_0\left( 1 - \frac{2}{9t^2\omega _0^2} \right).\] Thus the correction due to the cosmological expansion is \[\ddot r = - \frac{4r_0^3}{3t^4}\omega _0^2.\] Using $r_0 =1.5\cdot 10^{11}$m (distance from Earth to Sun), ${\omega _0}= 2\pi /T_0 \simeq 2 \cdot 10^{ - 7}s^{- 1}$ ($T_0$ is the Earth's year) and $t$ the age of the Universe, we obtain $\ddot r \simeq - 3.17 \cdot 10^{ - 47}$m/s$^2$. This quantity should be compared to gravitational acceleration of the Earth caused by the Sun $g = GM_\odot/r_0^2 \simeq 6 \cdot 10^{ - 3}$m/s$^2$, which is 44 orders of magnitude larger.