Difference between revisions of "Motivation and symmetries / Introduction"
(→Problem 10: Upper bound on frequency) |
|||
| Line 71: | Line 71: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;">Let us consider isolated systems of charges or masses that generate electromagnetic or gravitational waves correspondingly. The momentum of an isolated system is conserved, but existence of positive and negative charges (or just bodies with different rations $q/m$) allows one to create alternating dipole moment $\sum q_{i}\mathbf{r}_{i}$ while conserving the momentum $\sum m_{i}\mathbf{r}_{i}=const$. For gravity, however, the charge ''is'' the mass, which is the principle of equivalence lying at the heart of General Relativity, so that is impossible. This is the reason that in electromagnetic radiation the dominating term is usually the first one allowed, i.e. the dipole one, while for gravitational radiation the first possibly non-zero radiation term is the quadrupole one. | + | <p style="text-align: left;">Let us consider isolated systems of charges or masses that generate electromagnetic or gravitational waves correspondingly. The momentum of an isolated system is conserved, but existence of positive and negative charges (or just bodies with different rations $q/m$) allows one to create alternating dipole moment $\sum q_{i}\mathbf{r}_{i}$ while conserving the momentum $\sum m_{i}\mathbf{r}_{i}=const$. For gravity, however, the charge ''is'' the mass, which is the principle of equivalence lying at the heart of General Relativity, so that is impossible. This is the reason that in electromagnetic radiation the dominating term is usually the first one allowed, i.e. the dipole one, while for gravitational radiation the first possibly non-zero radiation term is the quadrupole one.</p> |
| − | < | + | |
<gallery widths=400px heights=200px> | <gallery widths=400px heights=200px> | ||
File:Dipole.png| | File:Dipole.png| | ||
</gallery> | </gallery> | ||
| − | Einstein writes of this in a letter to K.Shwarzshild (Feb 19, 1916): | + | |
| + | <p style="text-align: left;"> Einstein writes of this in a letter to K.Shwarzshild (Feb 19, 1916): | ||
"Thus there are no gravitational waves analogous to light waves. This probably is also related to the one-sidedness of the sign of scalar $T$, incidentally. (Nonexistence of the "dipole".)" | "Thus there are no gravitational waves analogous to light waves. This probably is also related to the one-sidedness of the sign of scalar $T$, incidentally. (Nonexistence of the "dipole".)" | ||
<br/> | <br/> | ||
| Line 94: | Line 95: | ||
\[\frac{dE}{dt}\sim | \[\frac{dE}{dt}\sim | ||
\frac{G}{c^5}\cdot | \frac{G}{c^5}\cdot | ||
| − | \dddot{Q}_{\alpha\beta} | + | {\dddot{Q}}_{\alpha\beta} |
| − | \dddot{Q}^{\alpha\beta},\] | + | {\dddot{Q}}^{\alpha\beta},\] |
where | where | ||
\[Q_{\alpha\beta}=\int d^3 x \; | \[Q_{\alpha\beta}=\int d^3 x \; | ||
| Line 106: | Line 107: | ||
<p style="text-align: left;">As seen above, from symmetry considerations the gravitational wave amplitude far from the source should be expressed in terms of time derivatives of the second mass (quadrupole) moment $h^{\mu\nu}\sim \frac{d^n}{dt^n}I^{\mu\nu}$, and we expect the energy flux to be quadratic in the wave amplitude. The luminosity $L_{GW}$ (total radiated power) in gravitational radiation should, therefore, also be quadratic in $I^{\mu\nu}$ and its time derivatives. | <p style="text-align: left;">As seen above, from symmetry considerations the gravitational wave amplitude far from the source should be expressed in terms of time derivatives of the second mass (quadrupole) moment $h^{\mu\nu}\sim \frac{d^n}{dt^n}I^{\mu\nu}$, and we expect the energy flux to be quadratic in the wave amplitude. The luminosity $L_{GW}$ (total radiated power) in gravitational radiation should, therefore, also be quadratic in $I^{\mu\nu}$ and its time derivatives. | ||
<br/> | <br/> | ||
| − | In units $G=c=1$ luminosity $L_{GW}$ is dimensionless. The third time derivative of $I^{\mu\nu}$ is also dimensionless; therefore, $L_{GW}$ must be a quadratic combination of $\dddot{I}^{\mu\nu}$. $L_{GW}$ also behaves as a scalar under rotations in space and so must be a quadratic scalar combination of $\dddot{I}_{\mu\nu}\dddot{I}^{\mu\nu}$ or $(\dddot{I}^\mu_\mu)^2$ . The precise combination is fixed by the demand that there is no radiation from a spherically symmetric system. In this case $I^{\mu\nu}\sim \delta^{\mu\nu}$ and the combination (reduced quadrupole momentum tensor) | + | In units $G=c=1$ luminosity $L_{GW}$ is dimensionless. The third time derivative of $I^{\mu\nu}$ is also dimensionless; therefore, $L_{GW}$ must be a quadratic combination of ${\dddot{I}}^{\mu\nu}$. $L_{GW}$ also behaves as a scalar under rotations in space and so must be a quadratic scalar combination of ${\dddot{I}}_{\mu\nu}{\dddot{I}}^{\mu\nu}$ or ${(\dddot{I}}^\mu_\mu)^2$ . The precise combination is fixed by the demand that there is no radiation from a spherically symmetric system. In this case $I^{\mu\nu}\sim \delta^{\mu\nu}$ and the combination (reduced quadrupole momentum tensor) |
\[Q^{\mu\nu}\equiv I^{\mu\nu} | \[Q^{\mu\nu}\equiv I^{\mu\nu} | ||
-\frac{1}{3}\delta^{\mu\nu}I_{\lambda}^{\lambda}\] | -\frac{1}{3}\delta^{\mu\nu}I_{\lambda}^{\lambda}\] | ||
vanishes. Consequently, | vanishes. Consequently, | ||
\[L_{GW}\sim | \[L_{GW}\sim | ||
| − | \dddot{Q}^{\mu\nu}\dddot{Q}_{\mu\nu}.\] | + | {\dddot{Q}}^{\mu\nu}{\dddot{Q}}_{\mu\nu}.\] |
The principle of equivalence states that locally gravitational field can always be turned to zero by an appropriate choice of reference frame. Therefore local energy density of a gravitational field will always depend on the coordinate frame (and gauge) and cannot be well-defined: it is not a tensor quantity. So in order to obtain some meaningful notion of $L_{GW}$, one has to average the obtained expression over spacetime volumes of the scales of the wavelength (which should be much less than curvature radius).</p> | The principle of equivalence states that locally gravitational field can always be turned to zero by an appropriate choice of reference frame. Therefore local energy density of a gravitational field will always depend on the coordinate frame (and gauge) and cannot be well-defined: it is not a tensor quantity. So in order to obtain some meaningful notion of $L_{GW}$, one has to average the obtained expression over spacetime volumes of the scales of the wavelength (which should be much less than curvature radius).</p> | ||
Latest revision as of 12:52, 15 January 2013
Contents
- 1 Problem 1: Decoupling time
- 2 Problem 2: Gravitational waves on curved background
- 3 Problem 3: No monopole radiation
- 4 Problem 4: No dipole gravitational radiation
- 5 Problem 5: Quadrupole formula from dimensional analysis
- 6 Problem 6: Natural luminosity
- 7 Problem 7: Natural luminosity from dimensional analysis
- 8 Problem 8: Quantum luminosity limit
- 9 Problem 9: Gravitationally bound systems
- 10 Problem 10: Upper bound on frequency
Problem 1: Decoupling time
Show that relic neutrinos can provide us with information on the Universe at temperatures less that 1 MeV (i.e. from the age of the order of seconds). What is the corresponding limit for gravitons?
The conditions for thermodynamic equilibrium for a given type of particles is that the rate of processes that maintain it $\Gamma$ is equal or greater that the Hubble rate $H$. For neutrino it take the form \[\Big(\frac{\Gamma}{H}\Big)_{\nu}> \frac{G_F^2 T^5}{T^2 /M_{Pl}} \approx \Big(\frac{T}{MeV}\Big)^3,\] where $G_F$ is the Fermi constant of weak interaction. Even weakly interacting neutrino cannot provide us with information of the Universe at temperatures \[T>1MeV,\ \quad t\sim 1.32 \left( \frac{MeV}{T} \right)^{2}\sim 1\sec.\] For the estimate of the corresponding quantity for gravitons we have to make replacement \[G_{F}\to G=\frac{1}{M_{Pl}^{2}}.\] Then we get \[\left( \frac{\Gamma }{H} \right)_{neutrino} >\left( \frac{T}{M_{Pl}}\right)^{3},\] so the decoupling for them takes place at Planck scales. Due to the ultimate weakness of gravitational interaction, the Universe became transparent for gravitons right from the times $\sim 10^{-43}s$ from the Big Bang, when the classical description we are using becomes in some measure applicable at all.
Problem 2: Gravitational waves on curved background
The basic theory of gravitational waves, discussed below, deals mostly with small perturbations on flat Minkowski background. Can this approximation be useful for studying waves on a non-trivial non-flat background, and if yes then in which cases?
Yes, if the characteristic curvature radius of the background $R$ is much larger than the spacial and temporal scales of the considered domain $L$, and the latter is much larger than the gravitational wave's wavelength.
Note also, that even when considering plane waves on Minkowski background, the nonlinear terms in Einstein's equations produce terms of the second order by the small perturbation. Those act as the energy-momentum of these gravitational waves, to the extent that energy can be assigned to gravity, and thus as the source of the gravitational field in the next order approximation. So beyond the first order linearized gravity the background is always curved.
Problem 3: No monopole radiation
Show that generation of either electromagnetic or gravitational monopole radiation is impossible.
Waves are propagating perturbation, which are produced by motion of the source of a certain type. Thus waves can be classified by the symmetries of the source. The one with the most symmetry is the motion that preserves spherical symmetry. Radiation of a source with spherical symmetry is usually called monopole radiation.
Monopole radiation can only be caused by a change in the source which is perfectly spherically symmetric. But purely radial oscillation as shown does not change the inverse-square law fields such as electromagnetism and gravity. A source simply disappearing would produce monopole radiation, but the conservation laws of charge and mass forbid this.
Problem 4: No dipole gravitational radiation
Show that dipole gravitational radiation is prohibited by the momentum conservation law.
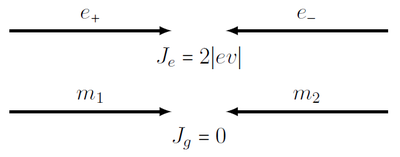
Let us consider isolated systems of charges or masses that generate electromagnetic or gravitational waves correspondingly. The momentum of an isolated system is conserved, but existence of positive and negative charges (or just bodies with different rations $q/m$) allows one to create alternating dipole moment $\sum q_{i}\mathbf{r}_{i}$ while conserving the momentum $\sum m_{i}\mathbf{r}_{i}=const$. For gravity, however, the charge is the mass, which is the principle of equivalence lying at the heart of General Relativity, so that is impossible. This is the reason that in electromagnetic radiation the dominating term is usually the first one allowed, i.e. the dipole one, while for gravitational radiation the first possibly non-zero radiation term is the quadrupole one.
Einstein writes of this in a letter to K.Shwarzshild (Feb 19, 1916):
"Thus there are no gravitational waves analogous to light waves. This probably is also related to the one-sidedness of the sign of scalar $T$, incidentally. (Nonexistence of the "dipole".)"
Thus D. Kennefick, in "Travelling at the Speed of Thought: Einstein and the Quest for Gravitational Waves" notes
"We see that Einstein... realized that there was no such thing as a "gravitational dipole". He deduces this from the well-known fact that there are no negative masses in nature, in the way that both negative and positive electric charges exist."
Problem 5: Quadrupole formula from dimensional analysis
Obtain, using dimensional analysis, the quadrupole formula for the energy loss by a system due to emission of gravitational waves \[\frac{dE}{dt}\sim \frac{G}{c^5}\cdot {\dddot{Q}}_{\alpha\beta} {\dddot{Q}}^{\alpha\beta},\] where \[Q_{\alpha\beta}=\int d^3 x \; ( x_\alpha x_\beta -\tfrac13 r^2 \delta_{\alpha\beta}) \rho(\mathbf{x}).\] is the reduced quadrupole moment of the system.
As seen above, from symmetry considerations the gravitational wave amplitude far from the source should be expressed in terms of time derivatives of the second mass (quadrupole) moment $h^{\mu\nu}\sim \frac{d^n}{dt^n}I^{\mu\nu}$, and we expect the energy flux to be quadratic in the wave amplitude. The luminosity $L_{GW}$ (total radiated power) in gravitational radiation should, therefore, also be quadratic in $I^{\mu\nu}$ and its time derivatives.
In units $G=c=1$ luminosity $L_{GW}$ is dimensionless. The third time derivative of $I^{\mu\nu}$ is also dimensionless; therefore, $L_{GW}$ must be a quadratic combination of ${\dddot{I}}^{\mu\nu}$. $L_{GW}$ also behaves as a scalar under rotations in space and so must be a quadratic scalar combination of ${\dddot{I}}_{\mu\nu}{\dddot{I}}^{\mu\nu}$ or ${(\dddot{I}}^\mu_\mu)^2$ . The precise combination is fixed by the demand that there is no radiation from a spherically symmetric system. In this case $I^{\mu\nu}\sim \delta^{\mu\nu}$ and the combination (reduced quadrupole momentum tensor)
\[Q^{\mu\nu}\equiv I^{\mu\nu}
-\frac{1}{3}\delta^{\mu\nu}I_{\lambda}^{\lambda}\]
vanishes. Consequently,
\[L_{GW}\sim
{\dddot{Q}}^{\mu\nu}{\dddot{Q}}_{\mu\nu}.\]
The principle of equivalence states that locally gravitational field can always be turned to zero by an appropriate choice of reference frame. Therefore local energy density of a gravitational field will always depend on the coordinate frame (and gauge) and cannot be well-defined: it is not a tensor quantity. So in order to obtain some meaningful notion of $L_{GW}$, one has to average the obtained expression over spacetime volumes of the scales of the wavelength (which should be much less than curvature radius).
Problem 6: Natural luminosity
Using the quadrupole formula, find the upper limit for gravitational luminosity of a source.
Let a non-spherical system have the characteristic parameters of mass, size, velocity and time scale $m,r,V,T$. Then $\dddot{Q}\sim mr^{2}/T^{3}$ and from the quadrupole formula \[L_{GW}\sim \frac{G}{c^5} \Big(\frac{m}{r}\Big)^{2}v^{6} \sim L_{0}\Big(\frac{r_{g}}{r}\Big)^{2} \Big(\frac{V}{c}\Big)^{6},\] where \[L_{0}\equiv \frac{c^5}{G} \approx 3.6\times {10}^{59}erg\] is the quantity which Einstein called natural luminosity. As $r\le {{r}_{g}},\ V\le c$, it is the upper limit to gravitational luminosity of any source of gravitational waves: \[L_{GW}\le L_{0}.\] Indeed, let us consider a process, in which all energy of some piece of matter $mc^2$ is converted into gravitational radiation during smallest possible time $t_{min}=r_{g}/c$. Then \[L=\frac{mc^2}{t_{min}}\sim \frac{c^5}{G}\equiv L_0.\]
Problem 7: Natural luminosity from dimensional analysis
Construct the limiting luminosity from dimensional analysis
Problem 8: Quantum luminosity limit
Why the upper limit on luminosity, obtained in General Relativity, should not change in the future quantum theory of gravitation?
The natural luminosity, which is also appear to be the ratio of Planck energy to Planck time \[L_{Pl}=\frac{\varepsilon_{Pl}}{t_{Pl}} =\frac{(\hbar c^5 /G)^{1/2}}{(G\hbar/c^5)^{1/2}} =\frac{c^5}{G}=L_{0},\] does not depend on $\hbar$.
Problem 9: Gravitationally bound systems
Estimate the gravitational luminosity for gravitationally bound systems
For a bound system \[V\sim \Big(\frac{Gm}{r}\Big)^{1/2}.\] Then using the result of problem on natural luminosity, we get \[L_{GW}\sim {{L}_{0}} \Big(\frac{r_{g}}{r}\Big)^{2} \Big(\frac{V}{c}\Big)^{6} =L_{0}\Big(\frac{r_{g}}{r}\Big)^{5}.\]
Problem 10: Upper bound on frequency
Estimate the upper bound of the gravitational wave frequency generated by a compact source with size $R$ and mass $M$.
The natural gravitational wave frequency generated by a compact source with size $R$ and mass $M$ is \[f_{GW}\sim \frac{1}{2\pi }\sqrt{GM/R^{3}}.\] As $R>r_{g}=2MG/c^{2}$, we can estimate the upper bound for the frequency of a compact source as \[f_{GW}(M)< \frac{1}{4\sqrt{2}\pi }\frac{c^{3}}{GM} \simeq 10^{4}\Big(\frac{M_{\odot}}{M}\Big)Hz.\] arXiv:astro-ph/0210481