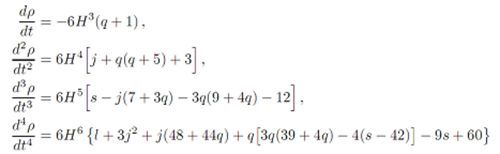Difference between revisions of "New Cosmography"
| (24 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | First section[[Cosmography]] | + | First section of → [[Cosmography]] |
__TOC__ | __TOC__ | ||
| Line 31: | Line 31: | ||
| − | <div id=""></div> | + | <div id="cs-3"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 3''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-3</p> |
| − | + | What is the reason for the statement that the cosmological parameters are model-independent? | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">The cosmographic parameters are model-independent quantities for the simple reason: these parameters are not functions of the EoS parameters $w$ or $w_{i} $ of the cosmic fluid filling the Universe in a concrete model.</p> |
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | <div id="cs-4"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 4''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-4</p> |
| − | + | Obtain the following relations between the deceleration parameter and Hubble's parameter | |
| − | <div class="NavFrame collapsed"> | + | $$q(t)=\frac{d}{dt}(\frac{1}{H})-1;\,\,q(z)=\frac{1+z}{H}\frac{dH}{dz}-1;\,\,q(z)=\frac{d\ln H}{dz}(1+z)-1.$$ |
| + | <!--<div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
<p style="text-align: left;"></p> | <p style="text-align: left;"></p> | ||
</div> | </div> | ||
| − | </div></div> | + | </div>--></div> |
| + | |||
| − | <div id=""></div> | + | <div id="cs-5"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 5''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-5</p> |
| − | + | Show that the deceleration parameter can be defined by the relation \[q=-\frac{d\dot{a}}{Hda} \] | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">\[q=-\frac{d\dot{a}}{Hda} =-\frac{\ddot{a}dt}{Hda} =-\frac{\ddot{a}}{aH^{2} } .\] |
| + | It corresponds to the standard definition of the deceleration parameter | ||
| + | \[q-\frac{\ddot{a}}{aH^{2} } .\]</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | <div id="cs-6"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 6''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-6</p> |
| − | + | Classify models of Universe basing on the two cosmographic parameters -- the Hubble parameter and the deceleration parameter. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">When the rate of expansion never changes, and $\dot{a}$ is constant, the scaling factor is proportional to time $t$ , and the deceleration term is zero. When the Hubble term is constant, the deceleration term $q$ is also constant and equal to $\mathrm{-}$1, as in the de Sitter and steady-state Universes. In most models of Universes the deceleration term changes in time. One can classify models of Universe on the basis of time dependence of the two parameters. All models can be characterized by whether they expand or contract, and accelerate or decelerate: |
| + | * (a) $H>0,\; q>0$: expanding and decelerating | ||
| + | * (b) $H>0,\; q<0$: expanding and accelerating | ||
| + | * (c) $H<0,\; q>0$: contracting and decelerating | ||
| + | * (d) $H<0,\; q<0$: contracting and accelerating | ||
| + | * (e) $H>0,\; q=0$: expanding, zero deceleration | ||
| + | * (f) $H<0,\; q=0$: contracting, zero deceleration | ||
| + | * (g) $H=0,\; q=0$ : static. | ||
| + | Of course, generally speaking, both the Hubble parameter and deceleration parameter can change their sign during the evolution. Therefore the evolving Universe can transit from one type to another. It is one of the basic tasks of cosmology to follow this evolution and clarify its causes. There is little doubt that we live in an expanding Universe, and hence only (a), (b), and (e) are possible candidates. Evidences in favor of the fact that the expansion is presently accelerating continuously grows in number and therefore the current dynamics belongs to type (b).</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | |
| + | <div id="cs-7"></div> | ||
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 7''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-7</p> |
| + | Show that the deceleration parameter $q$ can be presented in the form | ||
| + | $$q(x)=\frac{\dot{H}(x)}{H(x)}x-1;\,\,x=1+z$$ | ||
| + | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <div id="cs-8"></div> | |
| − | <div id=""></div> | + | |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 8''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-8</p> |
| + | Show that for the deceleration parameter the following relation holds: | ||
| + | $$q(a)=-\left(1+\frac{dH/dt}{H^2}\right)-\left(1+\frac{adH/da}{H}\right)$$ | ||
| + | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <div id=""></div> | + | <div id=""cs-9"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 9''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: "cs-9</p> |
| + | Show that $$\frac{dq}{d\ln (1+z)}=j-q(2q+1)$$ | ||
| + | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <div id="cs-10"></div> | |
| − | <div id=""></div> | + | |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 10''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-10</p> |
| − | + | Let \[C_{n} \equiv \gamma _{n} \frac{a^{(n)} }{aH^{n} } ,\] | |
| + | where $a^{(n)} $ is n-th time derivative of the scale factor, $n\ge 2$ , $\gamma _{2} =-1,\; \gamma _{n} =1$ äëÿ $n>2$ . Then$C_{2} =q,\; C_{3} =j,\; C_{4} =s\ldots $ Obtain $dC_{n} /d\ln (1+z)$ . | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">\[\begin{array}{l} {\frac{dC_{n} }{d\ln (1+z)} =-a\frac{dC_{n} }{da} =-\frac{1}{H} \frac{dC_{n} }{dt} ;} \\ {\frac{dC_{n} }{d\ln (1+z)} =-\gamma _{n} \left(\frac{a^{\left(n+1\right)} }{aH^{n+1} } -\frac{a^{\left(n\right)} }{aH^{n} } -n\frac{a^{(n)} \dot{H}}{aH^{n+2} } \right)=} \\ {=-\gamma _{n} \left(\frac{1}{\gamma _{n+1} } C_{n+1} -\frac{1}{\gamma _{n} } C_{n} -\frac{1}{\gamma _{n} } nC_{n} \frac{\dot{H}}{H^{2} } \right);} \\ {\frac{dC_{n} }{d\ln (1+z)} =-\frac{\gamma _{n} }{\gamma _{n+1} } C_{n+1} +C_{n} -nC_{n} (1+q)} \end{array}\]</p> |
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <div id="cs-11"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | '''Problem 11''' | ||
| + | <p style= "color: #999;font-size: 11px">problem id: cs-11</p> | ||
| + | Use result of the previous problem to find $dC_{n} /dt$. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">\[\frac{dC_{n} }{dt} =-H\frac{dC_{n} }{d\ln (1+z)} =H\left[\frac{\gamma _{n} }{\gamma _{n+1} } C_{n+1} -C_{n} +nC_{n} (1+q)\right]\]</p> |
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | <div id="cs12"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 12''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-12</p> |
| − | + | Use the general formula for $dC_{n} /dt$ obtained in the previous problem to obtain time derivatives of the cosmographic parameters $q,j,s,l$. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">\[\begin{array}{l} {\dot{q}=-H\left(j-2q^{2} -q\right),} \\ {\dot{j}=H\left[s+j(2+3q)\right],} \\ {\dot{s}=H\left[l+s(3+4q)\right],} \\ {\dot{l}=H\left[m+l(4+5q)\right]} \end{array}\]</p> |
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <div id="cs-13"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | '''Problem 13''' | ||
| + | <p style= "color: #999;font-size: 11px">problem id: cs-13</p> | ||
| + | Find derivatives of the cosmographic parameter w.r.t. the red shift. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Using results of the previous problem, one can transit from the time derivatives to the derivative w.r.t. the red shift according to the relation $\frac{d}{dz} =-\frac{1}{H(1+z)} \frac{d}{dt} $: |
| + | \[\begin{array}{l} {\frac{dH}{dz} =H\frac{1+q}{1+z} ,} \\ {\frac{dq}{dz} =\frac{j-2q^{2} -q}{1+z} ,} \\ {\frac{dj}{dz} =-\frac{s+j(2+3q)}{1+z} ,} \\ {\frac{ds}{dz} =-\frac{l+s(3+4q)}{1+z} ,} \\ {\frac{dl}{dz} =-\frac{m+l\left(4+5q\right)}{1+z} } \end{array}\]</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | <div id="cs-14"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 14''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-14</p> |
| − | + | Let $1+z=1/a\equiv x$. Find $q(x)$ and $j(x)$. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">It is easy to see that $\dot{H}=-H'H/a$ where $H'=dH/dx$. Then |
| + | \[q=-\frac{\dot{H}}{H^{2} } -1=\frac{H'}{H} x-1\] | ||
| + | Calculating $j$, making use of $a'=-a^{2} $, we obtain | ||
| + | \[j(x)=1-2\frac{H'}{H} x+\left(\frac{H'^{2} }{H^{2} } +\frac{H''}{H} \right)x^{2} \]</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <div id="cs-15"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | '''Problem 15''' | ||
| + | <p style= "color: #999;font-size: 11px">problem id: cs-15</p> | ||
| + | Express the derivatives $d^{2} H/dz^{2} $ , $d^{3} H/dz^{3} $ and $d^{4} H/dz^{4} $ in terms of the cosmographic parameters. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Using results of the two previous problems, one finds |
| + | \[\begin{array}{l} {\frac{d^{2} H}{dz^{2} } =\frac{j-q^{2} }{(1+z)^{2} } H,} \\ {\frac{d^{3} H}{dz^{3} } =\frac{H}{(1+z)^{3} } \left(3q^{2} +3q^{3} -4qi-3j-s\right)} \\ {\frac{d^{4} H}{dz^{4} } =\frac{H}{(1+z)^{4} } \left(-12q^{2} -24q^{3} -15q^{4} =32qj+25q^{2} j+7qs+12j-4j^{2} +8s+1\right)} \end{array}\]</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | <div id="cs-16"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 16''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-16</p> |
| − | + | Find decomposition of the inverse Hubble parameter $1/H$ in powers of the red shift $z$. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">\[\begin{array}{l} {\frac{d}{dz} \left(\frac{1}{H} \right)=-\frac{1}{H^{2} } \frac{dH}{dz} =-\frac{1+q}{1+z} \frac{1}{H} ;} \\ {\frac{d^{2} }{dz^{2} } \left(\frac{1}{H} \right)=2\left(\frac{1+q}{1+z} \right)^{2} \frac{1}{H} -\frac{j-q^{2} }{\left(1+z\right)^{2} } \frac{1}{H} =\frac{2+4q+3q^{2} -j}{(1+z)^{2} } \frac{1}{H} ;} \\ {\frac{1}{H(z)} =\frac{1}{H_{0} } \left[1-\left(1+q_{0} \right)z+\frac{2+4q_{0} +3q_{0}^{2} -j_{0} }{6} z^{2} +\ldots \right]} \end{array}\]</p> |
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | |
| + | <div id="cs-17"></div> | ||
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 17''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-17</p> |
| − | + | Obtain relations for transition from the time derivatives to that w.r.t. the red shift. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">\[\begin{array}{l} {\frac{d^{2} }{dt^{2} } =(1+z)H\left[H+(1+z)\frac{dH}{dz} \right]\frac{d}{dz} +(1+z)^{2} H^{2} \frac{d^{2} }{dz^{2} } ,} \\ {\frac{d^{3} }{dt^{3} } =-(1+z)H\left\{H^{2} +(1+z)^{2} \left(\frac{dH}{dz} \right)^{2} +(1+z)H\left[4\frac{dH}{dz} +(1+z)\frac{d^{2} H}{dz^{2} } \right]\right\}\frac{d}{dz} -3(1+z)^{2} H^{2} } \\ {\times \left[H+(1+z)\frac{dH}{dz} \right]\frac{d^{2} }{dz^{2} } -(1+z)^{3} H^{3} \frac{d^{3} }{dz^{3} } ,} \\ {\frac{d^{4} }{dt^{4} } =(1+z)H\left[H^{2} +11(1+z)H^{2} \frac{dH}{dz} +11(1+z)H\frac{dH}{dz} +(1+z)^{3} \left(\frac{dH}{dz} \right)^{3} +7(1+z)^{2} H\frac{d^{2} H}{dz^{2} } \right. } \\ {+\left. 4(1+z)^{3} H\frac{dH}{dz} \frac{d^{2} H}{d^{2} z} +(1+z)^{3} H^{2} \frac{d^{3} H}{d^{3} z} \right]\frac{d}{dz} +(1+z)^{2} H^{2} \left[7H^{2} +22H\frac{dH}{dz} +7(1+z)^{2} \left(\frac{dH}{dz} \right)^{2} \right. } \\ {+\left. 4H\frac{d^{2} H}{dz^{2} } \right]\frac{d^{2} }{dz^{2} } +6(1+z)^{3} H^{3} \left[H+(1+z)\frac{dH}{dz} \right]\frac{d^{3} }{dz^{3} } +(1+z)^{4} H^{4} \frac{d^{4} }{dz^{4} } +(1+z)^{4} H^{4} \frac{d^{4} }{dz^{4} } .} \end{array}\]</p> |
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | <div id="cs-18"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 18''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-18</p> |
| + | Can $dH^{n} /dz^{n} $ generally be expressed in terms of the cosmographic parameters? | ||
| + | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <div id=""></div> | + | <div id="cs-19"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 19''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-19</p> |
| − | + | Show that $$q(z)=frac 12 \frac{d\ln H^2}{d\ln(1+z)}$$ | |
| − | + | </div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <div id=""></div> | + | <div id="cs-20"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 20''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-20</p> |
| + | Show that the time derivatives of the Hubble's parameter can be expressed through the cosmographic parameters as follows: | ||
| + | $$\dot{H}=-H^2(1+q);$$ | ||
| + | $$\ddot{H}=H^3(j+3q+2)$$ | ||
| + | $$\dddot{H}=H^4\left(s-4j-3q(q+4)-6\right)$$ | ||
| + | $$\ddddot{H}=H^5\left(l-5s+10(q+2)j+30(q+2)+24\right)$$ | ||
| + | generally be expressed in terms of the cosmographic parameters? | ||
| + | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <div id=""></div> | + | <div id="cs-21"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 21''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-21</p> |
| − | + | Show that \[j=\frac{\ddot{H}}{H^{3} } +3\frac{\dot{H}}{H^{2} } +1\] | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Using results of the previous problem, we find |
| + | \[j=\frac{\ddot{H}}{H^{3} } -3q-2\] | ||
| + | Substituting | ||
| + | \[q=-\frac{\dot{H}}{H^{2} } -1\] | ||
| + | one finally obtains | ||
| + | \[j=\frac{\ddot{H}}{H^{3} } +3\frac{\dot{H}}{H^{2} } +1\]</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | <div id="cs-22"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 22''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-22</p> |
| − | + | Express total pressure in flat Universe through the cosmographic parameters. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Excluding the density $\rho $ from the Friedman equations |
| + | \[\begin{array}{l} {H=\frac{1}{3} \rho ,} \\ {\frac{\ddot{a}}{a} =H^{2} +\dot{H}=-\frac{1}{6} \left(\rho +3p\right)} \end{array}\] | ||
| + | one finds | ||
| + | \[p=-\left(3H^{2} +2\dot{H}\right)\] | ||
| + | Using the above obtained expression $\dot{H}=-H^{2} (1+q)$ , we obtain | ||
| + | \[p=-H^{2} \left(1-2q\right)\]</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <div id="cs-23"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | '''Problem 23''' | ||
| + | <p style= "color: #999;font-size: 11px">problem id: cs-23</p> | ||
| + | Express time derivatives $dp/dt,d^{2} p/dt^{2} ,d^{3} p/dt^{3} ,d^{4} p/dt^{4} $ through the cosmographic parameters. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Consequent differentiation w.r.t. time the expression $p=-H^{2} \left(1-2q\right)$ obtained in the previous problem using the expressions for the time derivatives of the cosmographic parameters |
| + | \[\begin{array}{l} {\dot{q}=-H\left(j-2q^{2} -q\right),} \\ {\dot{j}=H\left[s+j(2+3q)\right],} \\ {\dot{s}=H\left[l+s(3+4q)\right],} \\ {\dot{l}=H\left[m+l(4+5q)\right]} \end{array}\] | ||
| + | leads to | ||
| + | $$P=-H^2(1-2q)$$ | ||
| + | $$\frac{dP}{dt}=-2H^3(j-1)$$ | ||
| + | $$\frac{d^2P}{dt^2}=-2H^4(s-j+3q+3)$$ | ||
| + | $$\frac{d^3P}{dt^3}=-2H^5\left(l-j(1+q)-3q(7+2q)-2(6+s)\right)$$</p> | ||
| + | $$\frac{d^4P}{dt^4}=-2H^6\left(m-3l+j^2+12j(2+q)+3\left(20+s+q(48+q(27+2q)+s)\right)\right)$$</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | <div id="cs-24"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 24''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-24</p> |
| − | + | Express time derivatives $d\rho /dt,d^{2} \rho /dt^{2} ,d^{3} \rho /dt^{3} ,d^{4} \rho /dt^{4} $ through the cosmographic parameters. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Consequently differentiate the Friedman equation $\rho =3H^{2} $ and use expressions for the time derivatives of the cosmographic parameters to find[[File:image8.jpg|500px]]</p> |
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | |
| + | <div id="cs-25"></div> | ||
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 25''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-25</p> |
| − | + | Show that the accelerated growth of expansion rate $\dot{H}>0$ takes place under the condition $q<-1$. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">\[\dot{H}=-H^{2} (1+q),\quad \dot{H}>0\to q<-1\]</p> |
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | <div id="cs-26"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 26''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-26</p> |
| − | + | Consider the case of spatially flat Universe and express the scalar (Ricci ) curvature and its time derivatives in terms of the cosmographic parameters (-) | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Using the expression $R=-6\left(\frac{\ddot{a}}{a} +H^{2} \right)$ and definition of the deceleration parameter $q=-\frac{\ddot{a}}{aH^{2} } $ , one finds |
| + | \[R=-6H^{2} \left(1-q\right)\] | ||
| + | Using the expressions | ||
| + | \[\begin{array}{l} {\dot{H}=-H^{2} (1+q),} \\ {\dot{q}=-H\left(j-2q^{2} -q\right)} \end{array}\] | ||
| + | one obtains | ||
| + | \[\dot{R}=6H^{3} \left(2-j+q\right)\]</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <div id="cs-27"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | '''Problem 27''' | ||
| + | <p style= "color: #999;font-size: 11px">problem id: cs-27</p> | ||
| + | Following [O. Luongo and H. Quevedo, Self-accelerated universe induced by repulsive e$\boldsymbol{\mathrm{\textrm{?}}}$ects as an alternative to dark energy and modi?ed gravities, arXiv: (1507.06446)], introduce the parameter$\lambda \equiv -\frac{\ddot{a}}{a} =qH^{2} $ , so that $\lambda <0$ when the Universe is accelerating, whereas for $\lambda >0$ the Universe decelerates. Luongo and H. Quevedo showed, that the parameter $\lambda $ can be considered as an eigenvalue of the curvature tensor defined in special way. In particular, for FLRW metric the curvature tensor $R$ can be expressed as a (6 $\boldsymbol{\mathrm{\times}}$ 6)$\boldsymbol{\mathrm{-}}$matrix | ||
| + | \[R=diag\left(\lambda ,\lambda ,\lambda ,\tau ,\tau ,\tau \right),\quad \tau \equiv \frac{1}{3} \rho \] | ||
| + | The curvature eigenvalues reflect the behavior of the gravitational interaction and if gravity becomes repulsive in some regions, the eigenvalues must change accordingly; for instance, if repulsive gravity becomes dominant at a particular point, one would expect at that point a change in the sign of at least one eigenvalue. Moreover, if the gravitational field does not diverge at infinity, the eigenvalue must have an extremal at some point before it changes its sign. This means that the extremal of the eigenvalue can be interpreted as the onset of repulsion. Obtain the onset of repulsion condition in terms of cosmographic parameters. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">As mentioned above, the onset of repulsion is determined by an extremal of the eigenvalue, i.e.$\dot{\lambda }=0,$ |
| + | \[\lambda =qH^{2} \quad \to \quad \dot{\lambda }=\dot{q}H^{2} +2qH\dot{H}=0\] | ||
| + | Using the result of the previous problem for $\dot{q}$ and $\dot{H}$ we find that the repulsion onset condition $\dot{\lambda }=0$reduces to | ||
| + | \[j=-q.\]</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | <div id=""></div> | + | <div id="cs-28"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | '''Problem ''' | + | '''Problem 28''' |
| − | <p style= "color: #999;font-size: 11px">problem id: </p> | + | <p style= "color: #999;font-size: 11px">problem id: cs-28</p> |
| − | + | Represent results of the previous problem in terms of the Hubble parameter and its time derivatives. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Solving the system of equations |
| + | \[\begin{array}{l} {\dot{H}=-H^{2} (1+q),\quad } \\ {\ddot{H}=H^{3} \left(j+3q+2\right)} \end{array}\] | ||
| + | w.r.t. the variables $q$ and $j$ one finds, that the condition $j=-q$ transforms into | ||
| + | \[\frac{\ddot{H}}{H} =-2\dot{H}\]</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <div id="cs-29"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | '''Problem 29''' | ||
| + | <p style= "color: #999;font-size: 11px">problem id: cs-29</p> | ||
| + | Obtain the following integral relation between the Hubble's parameter and the deceleration parameter | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
Latest revision as of 00:39, 24 May 2016
First section of → Cosmography
Problem 1
problem id: cs-1
Using the cosmographic parameters introduced above, expand the scale factor into a Taylor series in time.
We can write the scale factor in terms of the present time cosmographic parameters: \[a(t)\sim 1+H_{0} \Delta t-\frac{1}{2} q_{0} H_{0}^{2} \Delta t^{2} +\frac{1}{6} j_{0} H_{0}^{3} \Delta t^{3} +\frac{1}{24} s_{0} H_{0}^{4} \Delta t^{4} +120l_{0} H_{0}^{5} \Delta t^{5} \] This decomposition describes evolution of the Universe on the time interval $\Delta t$ directly through the measurable cosmographic parameters. Each of them describes certain characteristic of the evolution. In particular, the sign of deceleration parameter $q$ indicates whether the dynamics is accelerated or decelerated. In other words, a positive\textbf{ }acceleration parameter indicates that standard gravity predominates over the other species, whereas a negative sign\textbf{ }provides a repulsive e\textbf{ff}ect which overcomes the standard attraction due to gravity. Evolution of the deceleration parameter is described by the jerk parameter $j$. In particular, a positive jerk parameter would\textbf{ }indicate that there exists a transition time when the Universe modifies its expansion. In the vicinity of this transition the modulus of deceleration parameters tends to zero and then changes its sign\textbf{. }The two terms, i.e., $q$ and $j$ fix the local dynamics, but they may be not sufficient to remove the degeneration between different cosmological models and one will need higher terms of the decomposition.
Problem 2
problem id: cs-2
Using the cosmographic parameters, expand the redshift into a Taylor series in time.
\[\begin{array}{l} {1+z=\left[\begin{array}{cc} {} & {1+H_{0} (t-t_{0} )-\frac{1}{2} q_{0} H_{0}^{2} (t-t_{0} )^{2} +\frac{1}{3!} j_{0} H_{0}^{3} \left(t-t_{0} \right)^{3} +\frac{1}{4!} s_{0} H_{0}^{4} \left(t-t_{0} \right)^{4} } \\ {} & {+\frac{1}{5!} l_{0} H_{0}^{5} \left(t-t_{0} \right)^{5} \; +{\rm O}\left(\left(t-t_{0} \right)^{6} \right)} \\ {} & {} \end{array}\right]^{-1} ;} \\ {z=H_{0} (t_{0} -t)+\left(1+\frac{q_{0} }{2} \right)H_{0}^{2} (t-t_{0} )^{2} +\cdots .} \end{array}\]
Problem 3
problem id: cs-3
What is the reason for the statement that the cosmological parameters are model-independent?
The cosmographic parameters are model-independent quantities for the simple reason: these parameters are not functions of the EoS parameters $w$ or $w_{i} $ of the cosmic fluid filling the Universe in a concrete model.
Problem 4
problem id: cs-4
Obtain the following relations between the deceleration parameter and Hubble's parameter $$q(t)=\frac{d}{dt}(\frac{1}{H})-1;\,\,q(z)=\frac{1+z}{H}\frac{dH}{dz}-1;\,\,q(z)=\frac{d\ln H}{dz}(1+z)-1.$$
Problem 5
problem id: cs-5
Show that the deceleration parameter can be defined by the relation \[q=-\frac{d\dot{a}}{Hda} \]
\[q=-\frac{d\dot{a}}{Hda} =-\frac{\ddot{a}dt}{Hda} =-\frac{\ddot{a}}{aH^{2} } .\] It corresponds to the standard definition of the deceleration parameter \[q-\frac{\ddot{a}}{aH^{2} } .\]
Problem 6
problem id: cs-6
Classify models of Universe basing on the two cosmographic parameters -- the Hubble parameter and the deceleration parameter.
When the rate of expansion never changes, and $\dot{a}$ is constant, the scaling factor is proportional to time $t$ , and the deceleration term is zero. When the Hubble term is constant, the deceleration term $q$ is also constant and equal to $\mathrm{-}$1, as in the de Sitter and steady-state Universes. In most models of Universes the deceleration term changes in time. One can classify models of Universe on the basis of time dependence of the two parameters. All models can be characterized by whether they expand or contract, and accelerate or decelerate:
- (a) $H>0,\; q>0$: expanding and decelerating
- (b) $H>0,\; q<0$: expanding and accelerating
- (c) $H<0,\; q>0$: contracting and decelerating
- (d) $H<0,\; q<0$: contracting and accelerating
- (e) $H>0,\; q=0$: expanding, zero deceleration
- (f) $H<0,\; q=0$: contracting, zero deceleration
- (g) $H=0,\; q=0$ : static.
Problem 7
problem id: cs-7
Show that the deceleration parameter $q$ can be presented in the form $$q(x)=\frac{\dot{H}(x)}{H(x)}x-1;\,\,x=1+z$$
Problem 8
problem id: cs-8
Show that for the deceleration parameter the following relation holds: $$q(a)=-\left(1+\frac{dH/dt}{H^2}\right)-\left(1+\frac{adH/da}{H}\right)$$
Problem 9
problem id: "cs-9
Show that $$\frac{dq}{d\ln (1+z)}=j-q(2q+1)$$
Problem 10
problem id: cs-10
Let \[C_{n} \equiv \gamma _{n} \frac{a^{(n)} }{aH^{n} } ,\] where $a^{(n)} $ is n-th time derivative of the scale factor, $n\ge 2$ , $\gamma _{2} =-1,\; \gamma _{n} =1$ äëÿ $n>2$ . Then$C_{2} =q,\; C_{3} =j,\; C_{4} =s\ldots $ Obtain $dC_{n} /d\ln (1+z)$ .
\[\begin{array}{l} {\frac{dC_{n} }{d\ln (1+z)} =-a\frac{dC_{n} }{da} =-\frac{1}{H} \frac{dC_{n} }{dt} ;} \\ {\frac{dC_{n} }{d\ln (1+z)} =-\gamma _{n} \left(\frac{a^{\left(n+1\right)} }{aH^{n+1} } -\frac{a^{\left(n\right)} }{aH^{n} } -n\frac{a^{(n)} \dot{H}}{aH^{n+2} } \right)=} \\ {=-\gamma _{n} \left(\frac{1}{\gamma _{n+1} } C_{n+1} -\frac{1}{\gamma _{n} } C_{n} -\frac{1}{\gamma _{n} } nC_{n} \frac{\dot{H}}{H^{2} } \right);} \\ {\frac{dC_{n} }{d\ln (1+z)} =-\frac{\gamma _{n} }{\gamma _{n+1} } C_{n+1} +C_{n} -nC_{n} (1+q)} \end{array}\]
Problem 11
problem id: cs-11
Use result of the previous problem to find $dC_{n} /dt$.
\[\frac{dC_{n} }{dt} =-H\frac{dC_{n} }{d\ln (1+z)} =H\left[\frac{\gamma _{n} }{\gamma _{n+1} } C_{n+1} -C_{n} +nC_{n} (1+q)\right]\]
Problem 12
problem id: cs-12
Use the general formula for $dC_{n} /dt$ obtained in the previous problem to obtain time derivatives of the cosmographic parameters $q,j,s,l$.
\[\begin{array}{l} {\dot{q}=-H\left(j-2q^{2} -q\right),} \\ {\dot{j}=H\left[s+j(2+3q)\right],} \\ {\dot{s}=H\left[l+s(3+4q)\right],} \\ {\dot{l}=H\left[m+l(4+5q)\right]} \end{array}\]
Problem 13
problem id: cs-13
Find derivatives of the cosmographic parameter w.r.t. the red shift.
Using results of the previous problem, one can transit from the time derivatives to the derivative w.r.t. the red shift according to the relation $\frac{d}{dz} =-\frac{1}{H(1+z)} \frac{d}{dt} $: \[\begin{array}{l} {\frac{dH}{dz} =H\frac{1+q}{1+z} ,} \\ {\frac{dq}{dz} =\frac{j-2q^{2} -q}{1+z} ,} \\ {\frac{dj}{dz} =-\frac{s+j(2+3q)}{1+z} ,} \\ {\frac{ds}{dz} =-\frac{l+s(3+4q)}{1+z} ,} \\ {\frac{dl}{dz} =-\frac{m+l\left(4+5q\right)}{1+z} } \end{array}\]
Problem 14
problem id: cs-14
Let $1+z=1/a\equiv x$. Find $q(x)$ and $j(x)$.
It is easy to see that $\dot{H}=-H'H/a$ where $H'=dH/dx$. Then \[q=-\frac{\dot{H}}{H^{2} } -1=\frac{H'}{H} x-1\] Calculating $j$, making use of $a'=-a^{2} $, we obtain \[j(x)=1-2\frac{H'}{H} x+\left(\frac{H'^{2} }{H^{2} } +\frac{H''}{H} \right)x^{2} \]
Problem 15
problem id: cs-15
Express the derivatives $d^{2} H/dz^{2} $ , $d^{3} H/dz^{3} $ and $d^{4} H/dz^{4} $ in terms of the cosmographic parameters.
Using results of the two previous problems, one finds \[\begin{array}{l} {\frac{d^{2} H}{dz^{2} } =\frac{j-q^{2} }{(1+z)^{2} } H,} \\ {\frac{d^{3} H}{dz^{3} } =\frac{H}{(1+z)^{3} } \left(3q^{2} +3q^{3} -4qi-3j-s\right)} \\ {\frac{d^{4} H}{dz^{4} } =\frac{H}{(1+z)^{4} } \left(-12q^{2} -24q^{3} -15q^{4} =32qj+25q^{2} j+7qs+12j-4j^{2} +8s+1\right)} \end{array}\]
Problem 16
problem id: cs-16
Find decomposition of the inverse Hubble parameter $1/H$ in powers of the red shift $z$.
\[\begin{array}{l} {\frac{d}{dz} \left(\frac{1}{H} \right)=-\frac{1}{H^{2} } \frac{dH}{dz} =-\frac{1+q}{1+z} \frac{1}{H} ;} \\ {\frac{d^{2} }{dz^{2} } \left(\frac{1}{H} \right)=2\left(\frac{1+q}{1+z} \right)^{2} \frac{1}{H} -\frac{j-q^{2} }{\left(1+z\right)^{2} } \frac{1}{H} =\frac{2+4q+3q^{2} -j}{(1+z)^{2} } \frac{1}{H} ;} \\ {\frac{1}{H(z)} =\frac{1}{H_{0} } \left[1-\left(1+q_{0} \right)z+\frac{2+4q_{0} +3q_{0}^{2} -j_{0} }{6} z^{2} +\ldots \right]} \end{array}\]
Problem 17
problem id: cs-17
Obtain relations for transition from the time derivatives to that w.r.t. the red shift.
\[\begin{array}{l} {\frac{d^{2} }{dt^{2} } =(1+z)H\left[H+(1+z)\frac{dH}{dz} \right]\frac{d}{dz} +(1+z)^{2} H^{2} \frac{d^{2} }{dz^{2} } ,} \\ {\frac{d^{3} }{dt^{3} } =-(1+z)H\left\{H^{2} +(1+z)^{2} \left(\frac{dH}{dz} \right)^{2} +(1+z)H\left[4\frac{dH}{dz} +(1+z)\frac{d^{2} H}{dz^{2} } \right]\right\}\frac{d}{dz} -3(1+z)^{2} H^{2} } \\ {\times \left[H+(1+z)\frac{dH}{dz} \right]\frac{d^{2} }{dz^{2} } -(1+z)^{3} H^{3} \frac{d^{3} }{dz^{3} } ,} \\ {\frac{d^{4} }{dt^{4} } =(1+z)H\left[H^{2} +11(1+z)H^{2} \frac{dH}{dz} +11(1+z)H\frac{dH}{dz} +(1+z)^{3} \left(\frac{dH}{dz} \right)^{3} +7(1+z)^{2} H\frac{d^{2} H}{dz^{2} } \right. } \\ {+\left. 4(1+z)^{3} H\frac{dH}{dz} \frac{d^{2} H}{d^{2} z} +(1+z)^{3} H^{2} \frac{d^{3} H}{d^{3} z} \right]\frac{d}{dz} +(1+z)^{2} H^{2} \left[7H^{2} +22H\frac{dH}{dz} +7(1+z)^{2} \left(\frac{dH}{dz} \right)^{2} \right. } \\ {+\left. 4H\frac{d^{2} H}{dz^{2} } \right]\frac{d^{2} }{dz^{2} } +6(1+z)^{3} H^{3} \left[H+(1+z)\frac{dH}{dz} \right]\frac{d^{3} }{dz^{3} } +(1+z)^{4} H^{4} \frac{d^{4} }{dz^{4} } +(1+z)^{4} H^{4} \frac{d^{4} }{dz^{4} } .} \end{array}\]
Problem 18
problem id: cs-18
Can $dH^{n} /dz^{n} $ generally be expressed in terms of the cosmographic parameters?
Problem 19
problem id: cs-19
Show that $$q(z)=frac 12 \frac{d\ln H^2}{d\ln(1+z)}$$
Problem 20
problem id: cs-20
Show that the time derivatives of the Hubble's parameter can be expressed through the cosmographic parameters as follows: $$\dot{H}=-H^2(1+q);$$ $$\ddot{H}=H^3(j+3q+2)$$ $$\dddot{H}=H^4\left(s-4j-3q(q+4)-6\right)$$ $$\ddddot{H}=H^5\left(l-5s+10(q+2)j+30(q+2)+24\right)$$ generally be expressed in terms of the cosmographic parameters?
Problem 21
problem id: cs-21
Show that \[j=\frac{\ddot{H}}{H^{3} } +3\frac{\dot{H}}{H^{2} } +1\]
Using results of the previous problem, we find \[j=\frac{\ddot{H}}{H^{3} } -3q-2\] Substituting \[q=-\frac{\dot{H}}{H^{2} } -1\] one finally obtains \[j=\frac{\ddot{H}}{H^{3} } +3\frac{\dot{H}}{H^{2} } +1\]
Problem 22
problem id: cs-22
Express total pressure in flat Universe through the cosmographic parameters.
Excluding the density $\rho $ from the Friedman equations \[\begin{array}{l} {H=\frac{1}{3} \rho ,} \\ {\frac{\ddot{a}}{a} =H^{2} +\dot{H}=-\frac{1}{6} \left(\rho +3p\right)} \end{array}\] one finds \[p=-\left(3H^{2} +2\dot{H}\right)\] Using the above obtained expression $\dot{H}=-H^{2} (1+q)$ , we obtain \[p=-H^{2} \left(1-2q\right)\]
Problem 23
problem id: cs-23
Express time derivatives $dp/dt,d^{2} p/dt^{2} ,d^{3} p/dt^{3} ,d^{4} p/dt^{4} $ through the cosmographic parameters.
Consequent differentiation w.r.t. time the expression $p=-H^{2} \left(1-2q\right)$ obtained in the previous problem using the expressions for the time derivatives of the cosmographic parameters \[\begin{array}{l} {\dot{q}=-H\left(j-2q^{2} -q\right),} \\ {\dot{j}=H\left[s+j(2+3q)\right],} \\ {\dot{s}=H\left[l+s(3+4q)\right],} \\ {\dot{l}=H\left[m+l(4+5q)\right]} \end{array}\] leads to $$P=-H^2(1-2q)$$ $$\frac{dP}{dt}=-2H^3(j-1)$$ $$\frac{d^2P}{dt^2}=-2H^4(s-j+3q+3)$$ $$\frac{d^3P}{dt^3}=-2H^5\left(l-j(1+q)-3q(7+2q)-2(6+s)\right)$$
$$\frac{d^4P}{dt^4}=-2H^6\left(m-3l+j^2+12j(2+q)+3\left(20+s+q(48+q(27+2q)+s)\right)\right)$$</p>
Problem 24
problem id: cs-24
Express time derivatives $d\rho /dt,d^{2} \rho /dt^{2} ,d^{3} \rho /dt^{3} ,d^{4} \rho /dt^{4} $ through the cosmographic parameters.
Problem 25
problem id: cs-25
Show that the accelerated growth of expansion rate $\dot{H}>0$ takes place under the condition $q<-1$.
\[\dot{H}=-H^{2} (1+q),\quad \dot{H}>0\to q<-1\]
Problem 26
problem id: cs-26
Consider the case of spatially flat Universe and express the scalar (Ricci ) curvature and its time derivatives in terms of the cosmographic parameters (-)
Using the expression $R=-6\left(\frac{\ddot{a}}{a} +H^{2} \right)$ and definition of the deceleration parameter $q=-\frac{\ddot{a}}{aH^{2} } $ , one finds \[R=-6H^{2} \left(1-q\right)\] Using the expressions \[\begin{array}{l} {\dot{H}=-H^{2} (1+q),} \\ {\dot{q}=-H\left(j-2q^{2} -q\right)} \end{array}\] one obtains \[\dot{R}=6H^{3} \left(2-j+q\right)\]
Problem 27
problem id: cs-27
Following [O. Luongo and H. Quevedo, Self-accelerated universe induced by repulsive e$\boldsymbol{\mathrm{\textrm{?}}}$ects as an alternative to dark energy and modi?ed gravities, arXiv: (1507.06446)], introduce the parameter$\lambda \equiv -\frac{\ddot{a}}{a} =qH^{2} $ , so that $\lambda <0$ when the Universe is accelerating, whereas for $\lambda >0$ the Universe decelerates. Luongo and H. Quevedo showed, that the parameter $\lambda $ can be considered as an eigenvalue of the curvature tensor defined in special way. In particular, for FLRW metric the curvature tensor $R$ can be expressed as a (6 $\boldsymbol{\mathrm{\times}}$ 6)$\boldsymbol{\mathrm{-}}$matrix \[R=diag\left(\lambda ,\lambda ,\lambda ,\tau ,\tau ,\tau \right),\quad \tau \equiv \frac{1}{3} \rho \] The curvature eigenvalues reflect the behavior of the gravitational interaction and if gravity becomes repulsive in some regions, the eigenvalues must change accordingly; for instance, if repulsive gravity becomes dominant at a particular point, one would expect at that point a change in the sign of at least one eigenvalue. Moreover, if the gravitational field does not diverge at infinity, the eigenvalue must have an extremal at some point before it changes its sign. This means that the extremal of the eigenvalue can be interpreted as the onset of repulsion. Obtain the onset of repulsion condition in terms of cosmographic parameters.
As mentioned above, the onset of repulsion is determined by an extremal of the eigenvalue, i.e.$\dot{\lambda }=0,$ \[\lambda =qH^{2} \quad \to \quad \dot{\lambda }=\dot{q}H^{2} +2qH\dot{H}=0\] Using the result of the previous problem for $\dot{q}$ and $\dot{H}$ we find that the repulsion onset condition $\dot{\lambda }=0$reduces to \[j=-q.\]
Problem 28
problem id: cs-28
Represent results of the previous problem in terms of the Hubble parameter and its time derivatives.
Solving the system of equations \[\begin{array}{l} {\dot{H}=-H^{2} (1+q),\quad } \\ {\ddot{H}=H^{3} \left(j+3q+2\right)} \end{array}\] w.r.t. the variables $q$ and $j$ one finds, that the condition $j=-q$ transforms into \[\frac{\ddot{H}}{H} =-2\dot{H}\]
Problem 29
problem id: cs-29
Obtain the following integral relation between the Hubble's parameter and the deceleration parameter
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id:
Problem
problem id: