Difference between revisions of "Schwarzschild black hole"
| Line 10: | Line 10: | ||
The Birkhoff's theorem$^{**}$ (1923) states, that this solution is unique up to coordinate transformations. The quantity $r_g$ is called the Schwarzschild radius, or gravitational radius, $M$ is the mass of the central body or black hole. | The Birkhoff's theorem$^{**}$ (1923) states, that this solution is unique up to coordinate transformations. The quantity $r_g$ is called the Schwarzschild radius, or gravitational radius, $M$ is the mass of the central body or black hole. | ||
| − | $^{*}$ K. Schwarzschild, On the gravitational field of a mass point according to Einstein's theory, ''Sitzungsber. Preuss. Akad. Wiss. Phys. Math. Kl.'', p.189 (1916) (there | + | $^{*}$ K. Schwarzschild, On the gravitational field of a mass point according to Einstein's theory, ''Sitzungsber. Preuss. Akad. Wiss. Phys. Math. Kl.'', p.189 (1916) (there's a translation of the original paper at [http://arxiv.org/abs/physics/9905030v1 arXiv:physics/9905030v1]; please disregard the abstract/foreword, which is incorrect). |
$^{**}$ G.D. Birkhoff, Relativity and Modern Physics, p.253, Harvard University Press, Cambridge (1923); | $^{**}$ G.D. Birkhoff, Relativity and Modern Physics, p.253, Harvard University Press, Cambridge (1923); | ||
Latest revision as of 10:02, 2 May 2013
The spherically symmetric solution of Einstein's equations in vacuum for the spacetime metric has the form$^{*}$
\begin{align}\label{Schw}
ds^{2}=h(r)\,dt^2-h^{-1}(r)\,dr^2-r^2 d\Omega^{2},
&\qquad\mbox{where}\quad
h(r)=1-\frac{r_g}{r};\quad r_{g}=\frac{2GM}{c^{2}};\\
d\Omega^{2}=d\theta^{2}+\sin^{2}\theta\, d\varphi^{2}&\;\text{is the metric of unit sphere.}\nonumber
\end{align}
The Birkhoff's theorem$^{**}$ (1923) states, that this solution is unique up to coordinate transformations. The quantity $r_g$ is called the Schwarzschild radius, or gravitational radius, $M$ is the mass of the central body or black hole.
$^{*}$ K. Schwarzschild, On the gravitational field of a mass point according to Einstein's theory, Sitzungsber. Preuss. Akad. Wiss. Phys. Math. Kl., p.189 (1916) (there's a translation of the original paper at arXiv:physics/9905030v1; please disregard the abstract/foreword, which is incorrect).
$^{**}$ G.D. Birkhoff, Relativity and Modern Physics, p.253, Harvard University Press, Cambridge (1923); J.T. Jebsen, "Ark. Mat. Ast. Fys." (Stockholm) 15, nr.18 (1921), see also arXiv:physics/0508163v2.
Contents
- 1 Simple problems
- 2 Symmetries and integrals of motion
- 3 Radial motion
- 4 Blackness of black holes
- 5 Orbital motion, effective potential
- 6 Miscellaneous problems
- 6.1 Problem 27: gravitational lensing
- 6.2 Problem 28: generalization of Newtonian potential
- 6.3 Problem 29: coordinate-invariant reformulation
- 6.4 Problem 30: surface gravity
- 6.5 Problem 31: uniqueness in exterior region
- 6.6 Problem 32: solution in a spherically symmetric void
- 6.7 Problem 33: shells
- 6.8 Problem 34: Einstein equations for spherically symmetric case
- 7 Different coordinates, maximal extension
Simple problems
Problem 1: local time
Find the interval of local time (proper time of stationary observer) at a point $(r,\theta,\varphi)$ in terms of coordinate time $t$, and show that $t$ is the proper time of an observer at infinity. What happens when $r\to r_{g}$?
The proper time of the stationary observer is $d\tau=ds|_{dr=d\theta=d\varphi=0}$: \[d\tau=\sqrt{g_{00}}\;dt=\sqrt{1-\frac{r_{g}}{r}}\;dt.\] At $r\to \infty$ it coincides with $dt$, so the coordinate time $t$ can be interpreted as the proper time of a "remote" observer. At $r\to r_g$ the local time flows slower and asymptotically stops. If one of two twins were to live some time at $r\approx r_g$, he will return to his remote twin having aged less (thought he might have acquired some grey hair due to constant fear of tumbling over the horizon).
Problem 2: measuring distances
What is the physical distance between two points with coordinates $(r_{1},\theta,\varphi)$ and $(r_{2},\theta,\varphi)$? Between $(r,\theta,\varphi_{1})$ and $(r,\theta,\varphi_{2})$? How do these distances behave in the limit $r_{1},r\to r_{g}$?
\[l_{r1-r2}=\int\limits_{r_1}^{r_2} \frac{dr}{\sqrt{1-\frac{r_g}{r}}};\quad l_{\varphi1-\varphi_2}=2\pi r|\varphi_1-\varphi_2|; \quad l_{\theta1-\theta_2}=2\pi r|\theta_1-\theta_2|.\]
Problem 3: the inner region
What would be the answers to the previous two questions for $r<r_g$ and why*? Why the Schwarzschild metric cannot be imagined as a system of "welded" rigid rods in $r<r_g$, as it can be in the external region?
This question is given not to be answered but to make one think of the answer. Correct questions and correct answers can be given in terms of a proper coordinate frame, which is regular both in $r>r_g$ and in $r<r_g$. Still, one can say something meaningful as is.
At $r<r_g$ we have $g_{00}<0$ and $g_{11}>0$, thus the $t$ coordinate is spatial and $r$ coordinate is temporal (!): \[ds^{2}=|h|^{-1}(r)dr^{2}-|h|(r)dt^{2} -r^{2}d\Omega^{2}.\] The metric therefore is nonstationary in this region, depending on the temporal coordinate $r$, but homogeneous, as there is no dependence on spatial coordinates. Then for an observer "at rest" with respect to this coordinate system we would have $dt=d\theta=d\varphi=0$, and thus \[d\tau^2=ds^2=-\frac{dr^{2}}{1-r_{g}/r}= \frac{r dr^{2}}{r_{g}-r}>0, \quad\Rightarrow\quad d\tau=\frac{\sqrt{r}dr}{\sqrt{r_{g}-r}}.\] An observer at rest with respect to the old coordinate system $dr=d\theta=d\varphi=0$, though, does not exist, as it would be $ds^{2}<0$ for him, which corresponds to spacelike geodesics (i.e. particles traveling faster than light). The last of the two questions cannot be answered without additional assumptions, because time $t$, which is the spatial coordinate now, in the two points is not given. The physical distance at $d\theta=d\varphi=dr=0$ is defined as \[dl^{2}=|h(r)|dt^2.\] It evidently depends on time $r$. This very fact that Schwarzschild metric is nonstationary at $r<r_g$, and that a stationary one does not exist in this region, leads to the absence of stationary observers and thus to the impossibility to imagine it "welded" of a system of stiff rods.
*This was actually not a very simple problem
Problem 4: acceleration
Calculate the acceleration of a test particle with zero velocity.
If a particle is at rest, its 4-velocity is $u^{\mu}=g_{00}^{-1/2}\delta^{\mu}_{0}$, where the factor is determined from the normalizing condition \[1=g_{\mu\nu}u^{\mu}u^{\mu}=g_{00}(u^{0})^{2}.\] Then the $4$-acceleration can be found from the geodesic equation: \begin{align*} a^{0}\equiv&\frac{du^0}{ds}=-{\Gamma^{0}}_{00}u^{0}u^{0}\sim {\Gamma^{0}}_{00}\sim \Gamma_{0,\,00}\sim (\partial_{0}g_{00}+\partial_{0}g_{00} -\partial_{0}g_{00})=0;\\ a^{1}\equiv&\frac{du^1}{ds} =-{\Gamma^{1}}_{00}u^{0}u^{0} =-g^{11}\Gamma_{1,\,00}\;g_{00}^{-1} =-(g_{00}g_{11})^{-1}\Gamma_{1,\,00}=\Gamma_{1,00}= \\ &=\tfrac{1}{2} (\partial_{0}g_{10}+\partial_{0}g_{10} -\partial_{1}g_{00}) =-\frac{1}{2}\frac{dg_{00}}{dr} =-\frac{h'}{2} =\frac{r_{g}}{2r^2}. \end{align*} The scalar acceleration $a$ is then equal to \[a^{2}=-g_{11}(a^{1})^{2}=\frac{(h')^{2}}{4h} =-\frac{r_{g}^{2}}{4 r^4} \Big(1-\frac{r_g}{r}\Big)^{-1}\] and tends to infinity when we approach the horizon.
Problem 5: Schwarzschild is a vacuum solution
Show that Schwarzschild metric is a solution of Einstein's equation in vacuum.
Straightforward calculation of Christoffel symbols and Ricci tensor yields the vacuum Einstein equation $R_{\mu\nu}=0$.
Symmetries and integrals of motion
For background on Killing vectors see problems K1, K2, K3 of chapter 2.
Problem 6: timelike Killing vector
What integral of motion arises due to existence of a timelike Killing vector? Express it through the physical velocity of the particle.
If a Killing vector field is timelike we can use the coordinate frame in which $K^\mu$ is the unitary vector of the time coordinate (see problem K2 of chapter 2.) $K^{\mu}=(1,0,0,0)$, while the spacelike basis vectors are orthogonal to it. Then the integral of motion is energy in the corresponding (stationary) frame $p_{\mu}K^{\mu}=p_{0}\equiv\varepsilon/c$. Using the result u0, which holds for arbitrary gravitational field, we obtain the expression for energy, which is the integral of motion in a stationary metric \begin{equation}\label{EnergyStat} \varepsilon=mc^{2}u_{0}= mc^{2}\sqrt{g_{00}}\cdot\gamma= \frac{mc^{2}\sqrt{g_{00}}} {\sqrt{1-\frac{v^2}{c^2}}}.\end{equation}
Problem 7: Killing vectors of a sphere
Derive the Killing vectors for a sphere in Cartesian coordinate system; in spherical coordinates.
Killing vectors correspond to infinitesimal transformations that leave the metric invariant. Considering a two-dimensional sphere embedded in the tree-dimensional space, we can see that its symmetries are rotations. Three of them are independent: the rotations in each of the three coordinate planes. Let us consider an infinitesimal rotation in the plane $XY$: $dx=yd\lambda,\; dy=-xd\lambda$. Thus the Killing vector is* \[K_{1}=x\partial_y-y\partial_x.\] Using the spherical coordinates \[x=\sin\theta\cos\varphi;\quad y=\sin\theta\sin\varphi;\quad z=\cos\theta,\] we obtain $\partial_{x}=-\frac{\sin\varphi}{\sin\theta}\partial_\varphi$, $\partial_y=\frac{\cos\varphi}{\sin\theta}\partial_\varphi$, and therefore $K_{1}=\partial_{\varphi}$. Considering rotations in plains $XZ$ and $YZ$ in the same way, in the end we obtain \[\left\{\begin{array}{l} K_{1}=x\partial_{y}-y\partial_{x}=\partial_{\varphi}\\ K_{2}=z\partial_{x}-x\partial_{z}= \cos\varphi\;\partial_{\theta}-\cot\theta\sin\varphi\;\partial_\varphi\\ K_{3}=z\partial_{y}-y\partial_{x}= \sin\varphi\;\partial_{\theta}+\cot\theta\cos\varphi\;\partial_\varphi\;. \end{array}\right.\]
*Hereafter we use the following notation: a 4-vector $A$ is $A=A^{\mu}\partial_{\mu}$, where $\partial_{\mu}\equiv\partial/\partial x_{\mu}$ is the "coordinate" basis, $A^{\mu}$ the coordinates of $A$ in this basis; it is not hard to verify that transformation laws for $A^\mu$ and $\partial_{\mu}$ are adjusted so that $A$ is a quantity that does not depend on a coordinate frame. This also enables us to conveniently recalculate $A^\mu$ when we change the basis. For more detail see e.g. the textbook by Carroll:
Carroll S., Spacetime and geometry: an introduction to General Relativity. AW, 2003, ISBN 0805387323
Problem 8: spherical symmetry of Schwarzshild
Verify that in coordinates $(t,r,\theta,\varphi)$ vectors \[ \begin{array}{l} \Omega^{\mu}=(1,0,0,0),\\ R^{\mu}=(0,0,0,1),\\ S^{\mu}=(0,0,\cos\varphi,-\cot\theta\sin\varphi),\\ T^{\mu}=(0,0,-\sin\varphi,-\cot\theta\cos\varphi) \end{array}\] are the Killing vectors of the Schwarzschild metric.
Vectors $\Omega^\mu$ and $R^\mu$ are Killing vectors because the metric does not depend explicitly either on $t$ or on $\varphi$. The last two correspond to the spherical symmetry (see previous problem). We can also check directly that they obey the Killing equation by evaluating the Christoffel symbols for the Schwarzschild metric.
Problem 9: planar motion
Show that existence of Killing vectors $S^\mu$ and $T^\mu$ leads to motion of particles in a plane.
The integrals of motion corresponding to $S^\mu$ and $T^\mu$ are \begin{align*} S=u_{\mu}S^{\mu}=& \;u_{2}\cos\varphi-u_{3}\cot\theta\sin\varphi;\\ T=u_{\mu}T^{\mu}=& -u_{2}\sin\varphi-u_{3}\cot\theta\cos\varphi. \end{align*} Let us align the coordinate frame in such a way that the initial conditions are \[\theta|_{t=0}=\pi/2;\quad u_{2}|_{t=0}\equiv u_{\theta}|_{t=0}=0.\] Then $S$ and $T$ are zero: \[u_{2}\cos\varphi=u_{3}\cot\theta\sin\varphi;\qquad u_{2}\sin\varphi=-u_{3}\cot\theta\cos\varphi.\] Taking the square and adding the two equations, and also multiplying them, we obtain \[\left\{\begin{array}{l} u_{2}^{2}=u_{3}^{2}\cot^{2}\theta,\\ u_{2}^{2}\sin\varphi\cos\varphi= -u_{3}^{2}\cot^{2}\theta\sin\varphi\cos\varphi \end{array}\right.\quad\Rightarrow\quad u_{3}^{2}\sin\varphi\cos\varphi \cdot\cot^{2}\theta=0.\] Then either $\varphi=const$, which means that $u_{3}=u_{2}=0$ and the motion is radial, or $\cot^{2}\theta=0$ and the motion takes place in the plane $\theta=\pi/2$.
Problem 10: stability of planar motion
Show that the particles' motion in the plane is stable.
Conservation of $u_{\mu}R^{\mu}$ means that $R\equiv u_{3}\equiv\varphi'=const$. It is not hard to derive from the expressions for $S$ and $T$ that \begin{align*} &S\sin\varphi+T\cos\varphi=R\cot\theta,\\ &S\cos\varphi-T\sin\varphi=u_2. \end{align*} Taking the square and adding up, we are led to \[u_2^2 =S^2+T^2+R^2-\frac{R^2}{\sin^2 \theta},\] then on differentiating we obtain \[u'_{2}=R^2 \frac{\cos\theta}{\sin^{2}\theta}.\] Let the trajectory deviate slightly from the plane $\theta=\pi/2$. Then $\theta=\pi/2+\delta\theta$ and \[(\delta\theta)''=u'_{2} =R^2 \frac{\cos\theta}{\sin^{2}\theta} \approx -R^2 \delta\theta,\] therefore $\theta$ oscillates around the stable point $\pi/2$.
Problem 11: remaining integrals of motion
Write down explicitly the conserved quantities $p_{\mu}\Omega^{\mu}$ and $p_{\mu}R^{\mu}$ for movement in the plane $\theta=\pi/2$.
The first integral of motion is, up to a multiplier, the energy (see Eq. EnergyStat): \begin{equation}\label{SchwInt-E1} E=\Omega_{\mu}u^{\mu}= g_{00}\frac{dx^{0}}{d\lambda}=h\frac{dt}{d\lambda}= \left(1-\frac{r_g}{r}\right)\frac{dt}{d\lambda},\end{equation} where $\lambda$ is the geodesic parameter: for a massive particle we can always choose the natural parametrization $d\lambda=ds=\gamma^{-1}\sqrt{g_{00}}\,dt$ (see Eq. IntervalStaticCase) so that $E$ is energy per unit mass; recovering the multipliers, for true energy we obtain \begin{equation}\label{SchwInt-E2} \varepsilon_{m}\equiv mcE= mc^{2}\sqrt{g_{00}}\,\gamma= mc^{2}\sqrt{h}\,\gamma= mc^{2}\sqrt{\frac{1-r_{g}/r}{1-v^{2}/c^{2}}}.\end{equation} The second integral of motion is the angular momentum (per unit mass also, and the sign is chosen so that in the Newtonian limit we obtain the usual angular momentum) \begin{equation}\label{SchwInt-L1} L=-R_{\mu}u^{\mu}=-g_{33}\frac{dx^{3}}{d\lambda}= r^{2}\sin^{2}\theta\frac{d\varphi}{d\lambda}= r^{2}\frac{d\varphi}{d\lambda}.\end{equation} For a massive particle we choose $\lambda=s$, then $d\lambda=ds=\gamma^{-1}\sqrt{g_{00}}\,dt$ and \begin{equation}\label{SchwInt-L2} l_{m}\equiv mL= mr^{2}\dot{\varphi} \sqrt{g_{00}}\gamma= m r^{2}\dot{\varphi} \sqrt{\frac{1-r_{g}/r}{1-v^{2}/c^{2}}}.\end{equation} Note that conservation of $l_m$ is a generalization to the relativistic case of the second Kepler's law on the sweeping of equal areas per unit time $r^{2}\dot{\varphi}=const$.
Problem 12: work and mass
What is the work needed to pull a particle from the horizon to infinity? Will a black hole's mass change if we drop a particle with zero initial velocity from immediate proximity of the horizon?
At $r\gg r_g$ we'll have $\varepsilon_{m}=mc^{2}$, while near the horizon $\varepsilon_{m}\to 0$. The difference is the work needed to pull the particle away from the horizon to infinity, and it equals the rest mass (energy) of the particle. No, it will not change, because the energy of the falling particle is zero.
Radial motion
Consider a particle's radial motion: $\dot{\varphi}=\dot{\theta}=0$. In this problem one is especially interested in asymptotes of all functions as $r\to r_{g}$.
Let us set $c=1$ here and henceforth measure time in the units of length, so that $x^{0}=t$, $\beta=v$, etc., and introduce the notation \[h(r)\equiv g_{00}(r)=-\frac{1}{g_{11}(r)}= 1-\frac{r_{g}}{r} \underset{r\to r_g+0}{\longrightarrow}+0.\]
Problem 13: null geodesics
Derive the equation for null geodesics (worldlines of massless particles).
Equation of null curve is $ds^2=0$. Substituting the metric with $d\theta=d\varphi=0$, we get \[dt=\pm dr\,\sqrt{-\frac{g_{11}}{g_{00}}} =\pm\frac{dr}{h}.\] On integration, we obtain \begin{equation}\label{Schw-NullGeodesic} \pm t=r+r_{g}\ln|r-r_{g}|+const.\end{equation} Due to symmetry it is also a geodesic. This can be verified by evaluating the Christoffel symbols for the Schwarzschild metric and writing down the geodesic equatoin in explicit form.
Problem 14: geodesic motion of massive particle
Use energy conservation to derive $v(r)$, $\dot{r}(r)=dr/dt$, $r(t)$ for a massive particle. Initial conditions: $g_{00}|_{\dot{r}=0}=h_{0}$ (the limiting case $h_{0}\to 1$ is especially interesting and simple).
In the radial case the physical velocity $v$ is expressed through the $4$-velocity $u^{\mu}=(u^{0},u^{1},0,0)$ as \begin{equation}\label{Schw-v(u)} \beta^{2}=\frac{dx^{\alpha}dx_{\alpha}}{d\tau^{2}}= \frac{-g_{11}(dx^{1})^{2}}{g_{00}(dx^{0})^{2}}= h^{-2}\Big(\frac{u^1}{u^0}\Big)^2= \Big(\frac{\dot{r}}{h}\Big)^2,\end{equation} where dot denotes differentiation by coordinate time $t$, and thus the energy conservation law (see (\ref{SchwInt-E2})) takes the form \[const=\Big(\frac{\varepsilon}{mc^2}\Big)^{2}= h\gamma^{2}=\frac{h}{1-\dot{r}^{2}/h^2}.\] Initial condition fixes the constant*: \begin{equation}\label{Schw-h0} \dot{r}\sim v|_{r_{0}}=0\quad \Rightarrow\quad \Big(\frac{\varepsilon}{mc^2}\Big)^{2} =g_{00}(r_{0})=h(r_0)=1-\frac{r_{g}}{r_{0}} \equiv h_{0},\end{equation} so for the physical velocity we get \begin{equation}\label{SchwRad-V} \gamma^{2}=\frac{h_{0}}{h(r)} \underset{r\to r_{g}}{\longrightarrow}\infty; \quad \frac{v}{c}\equiv\beta= \sqrt{1-\gamma^{-2}}= \sqrt{1-\frac{h}{h_{0}}} \underset{r\to r_{g}}{\longrightarrow}1.\end{equation} It tends to infinity close to the horizon! At the same time, as $v^{2}=\dot{r}^{2}/h^{2}$ from (\ref{Schw-v(u)}), the coordinate velocity \begin{equation}\label{Schw-dotR} \Big|\frac{dr}{dt}\Big|=vh=h \sqrt{1-\frac{h}{h_{0}}}= \Big(1-\frac{r_{g}}{r}\Big) \sqrt{1-\frac{1-\frac{r_{g}}{r}}{1-\frac{r_{g}}{r_{0}}}} \underset{r\to r_{g}}{\thicksim}h\to 0\end{equation} tends to zero. After integration we obtain $t(r)$: \begin{equation}\label{Schw-t(r)} const\pm t=\int\limits_{r}^{r_{0}} \frac{dr}{vh}= \int\limits_{r}^{r_{0}}\frac{rdr}{r-r_{g}} \bigg[1-\frac{1-r_{g}/r}{1-r_{g}/r_{0}}\bigg]^{-1/2} \underset{\substack{r\approx r_{g}\\r_{0}\gg r_{g}}} {\approx}\int\limits_{r}^{r_{0}} \frac{r\,dr}{r-r_{g}}=r+r_{g}\ln|r-r_{g}|.\end{equation} As should be expected, the asymptote is the same as for the null geodesics (for $r_{0}\gg r_{g}$).
*Note that $r_0$ has the meaning of a turning point only for finite motion; this, however, does not prevent us from using the same notation in the non-finite case. Then $r_0$ is determined from $\varepsilon$ by the same formula and takes negative values, while $h_{0}>1$.
Problem 15: radial motion in terms of proper time
Show that the equation of radial motion in terms of proper time of the particle is the same as in the non-relativistic Newtonian theory. Calculate the proper time of the fall from $r=r_0$ to the center. Derive the first correction in $r_{g}/r$ to the Newtonian result. Initial velocity is zero.
The particle's proper time interval $\tau$ is $d\tau=\gamma^{-1} d\hat{t}$, where $d\hat{t}=\sqrt{h}dt$ is local time. Then \begin{equation}\label{ShwRad-tau} \tau=\int dt \gamma^{-1}\sqrt{h}= \int\limits_{r}^{r_{0}} \frac{dr}{\gamma v\sqrt{h}}= \int\limits_{r}^{r_{0}} \frac{dr}{v \sqrt{h_{0}}}= \int\limits_{r}^{r_{0}} \frac{dr}{\sqrt{h_{0}-h}}= \int\limits_{r}^{r_{0}} \frac{dr}{\sqrt{\frac{r_{g}}{r_{0}}- \frac{r_{g}}{r}}}.\end{equation} On the other hand, in the Newtonian approach from energy conservation we obtain in the same way that \[(\dot{r})^{2}=2(E-U)=2\;\Big(E+\frac{GM}{r}\Big) =\frac{r_{g}}{r}-\frac{r_{g}}{r_{0}},\] which gives us the same equation of motion. We see that the integral is regular at $r=r_{g}$, is finite and converges even at $r\to 0$. It is not hard to evaluate: \begin{equation}\label{Schw-TauParametric} \tau=\frac{r_0}{2}\sqrt{\frac{r_0}{r_g}} (\eta+\sin\eta),\qquad r=\frac{r_0}{2}(1+\cos\eta),\qquad \eta\in(0,\pi). \end{equation} The proper time of reaching the singularity $r=0$ is therefore \[\tau_{f}=\frac{\pi}{2}r_{0} \sqrt{\frac{r_{0}}{r_{g}}}.\] The integral (\ref{Schw-t(r)}) for $t(r)$ can be rewritten as \[t(r)=\int \frac{dr}{vh}=\sqrt{h_{0}} \int\frac{dr}{\sqrt{h_{0}-h}}\cdot \frac{1}{h}= \underbrace{\sqrt{1-\frac{r_{g}}{r_{0}}}} _{\text{correction 1}}\, \underbrace{\int\!\frac{dr}{\sqrt{\frac{r_g}{r}-\frac{r_g}{r_0}}}}_{\tau(r)} \cdot \underbrace{\frac{1}{1-\frac{r_g}{r}}} _{\text{correction 2}}.\] Now we see that the first factor gives the correction taking into account time dilation in the initial point $r_0$, while the second correction accounts for local time dilation and proper time dilation due to acceleration. If the second factor is close to unity, we can expand it in powers of $r_{g}/r$ and obtain \[t=\sqrt{1-\frac{r_g}{r_0}}\;\; \big[\tau+\Delta\tau\big], \quad\text{where}\quad \Delta\tau=\int \frac{dr\,r_{g}/r} {\sqrt{\frac{r_g}{r}-\frac{r_g}{r_0}}}.\] On integrating, we can express $\Delta\tau$ through $\eta$ (\ref{Schw-TauParametric}), and thus derive the equation of motion in the form analogous to (\ref{Schw-TauParametric}), but with the correction term \begin{equation}\label{Schw-TauParametric2} \tau=\frac{r_0}{2}\sqrt{\frac{r_0}{r_g}}\; \Big([1+\tfrac{r_g}{r_0}]\eta+\sin\eta\Big),\qquad r=\frac{r_0}{2}(1+\cos\eta). \end{equation} Evidently, this approximation works only for $r\gg r_{g}$.
Problem 16: ultra-relativistic limit
Derive the equations of radial motion in the ultra-relativistic limit.
In the relativistic limit we should assume $\gamma\gg1$ (near $r_{g}$ this always holds), thus $v\to 1$, and from (\ref{Schw-dotR}) we get \[\frac{dr}{dt}\approx h\quad \Rightarrow\quad t=\int \frac{dr}{h}.\] This is, as should be expected, the null geodesic equation.
Problem 17: communication from near the black hole
A particle (observer) falling into a black hole is emitting photons, which are detected on the same radial line far away from the horizon (i.e. the photons travel from emitter to detector radially). Find $r$, $v$ and $\dot{r}$ as functions of the signal's detection time in the limit $r\to r_g$.
The geodesics describing light signals propagating away from the horizon are given by the equation (\ref{Schw-NullGeodesic}) with the plus sign: \begin{equation}\label{Schw-tLambda} t=r+r_{g}\ln|r-r_{g}|+t_{\Lambda},\end{equation} where parameter $t_\Lambda$ parametrizes this family of geodesics and gives the difference in coordinate times of signals' registration at a given $r$. At $r\gg r_g$ this is also the proper time of the remote detector. Then \begin{equation}\label{Schw-dtL(dr)} dt_{\Lambda}=dt-\frac{r_{g}dr}{r-r_{g}}= dt-\frac{r_{g}dr}{rh}= -\frac{dr}{vh}-\frac{r_{g}dr}{rh}= -\frac{dr}{h}\Big(\frac{1}{v}+\frac{r_{g}}{r}\Big).\end{equation} As both $v$ and $r_{g}/r$ tend to unity near the horizon, the integral diverges logarithmically, twice faster than the one for $t(r)$. The meaning of this number is the following: as $r\to r_{g}$, the geodesics of massive and massless particles asymptotically coincide, and it takes the light as much time to "escape" the potential well as it takes the particle to fall in. Asymptotically we obtain \begin{equation}\label{Schw-r(tL)} -t_{\Lambda}\approx 2\int\limits^{r} \frac{rdr}{r-r_{g}}\approx 2r_{g}\ln|r-r_{g}| \approx 2t(r)\quad\Rightarrow\quad r(t_{\Lambda})-r_{g}\sim r_{g} e^{-t_{\lambda}/2r_{g}};\end{equation} also $\gamma=h_{0}/h\approx r_{g}/(r-r_{g})$, $v(r)=\sqrt{1-h/h_{0}}\approx 1-(r-r_{g})/2r_{g}$, and $\dot{r}\approx h$, thus \begin{equation}\label{Schw-v(tL)} \gamma\sim e^{t_{\Lambda}/2r_{g}};\qquad (1-v)\sim {\textstyle\frac{1}{2}} e^{-t_{\Lambda}/2r_{g}}; \qquad \dot{r}\sim e^{-t_{\Lambda}/2r_{g}}.\end{equation}
Blackness of black holes
A source radiates photons of frequency $\omega_i$, its radial coordinate at the time of emission is $r=r_{em}$. Find the frequency of photons registered by a detector situated at $r=r_{det}$ on the same radial line in different situations described below. By stationary observers here, we mean stationary in the static Schwarzschild metric; "radius" is the radial coordinate $r$.
Problem 18: stationary source and detector
The source and detector are stationary.
The integral of motion that conserves along the light ray due to the timelike Killing vector $\Omega^{\mu}=\partial_{t}$ is energy (up to a factor): \begin{equation}\label{Schw-OmegaConst} const\equiv\omega_{0}= g_{\mu\nu}\Omega^{\mu}k^{\nu}= g_{00}k^{0}=hk^{0}.\end{equation} For a static observer $u^{\mu}=(u^{0},0,0,0)$, while \begin{equation}\label{Schw-u0} 1=u^{\mu}u_{\mu}=g_{\mu\nu}u^{\mu}u^{\nu}= g_{00}(u^{0})^{2}\quad\Rightarrow\quad u^{0}=h^{-1/2}.\end{equation} Therefore the frequency registered by this static observer is \begin{equation}\label{Schw-omegastat} \omega_{stat}=g_{\mu\nu}u^{\mu}_{stat}k^{\nu}= g_{00}u^{0}_{stat}k^{0}=\sqrt{g_{00}}k^{0}= \sqrt{h}k^{0}=\omega_{0}h^{-1/2}.\end{equation} Then \begin{equation}\label{Schw-RedShift0} \omega_{0}=\omega_{stat}(r)\sqrt{h(r)}=const,\end{equation} so we obtain \begin{equation}\label{Schw-RedShift} \omega_{det}=\omega_{em} \sqrt{\frac{g_{00}(r_{em})}{g_{00}(r_{det})}}.\end{equation} This is gravitational redshift.
Problem 19: free-falling source
The source is falling freely without initial velocity from radius $r_0$; it flies by the stationary detector at the moment of emission.
It is educative to derive the Doppler effect from analogous considerations. Let us consider an emitter (detector) moving radially with physical velocity $v$ (see. (\ref{Schw-v(u)})). From the normalizing condition \begin{equation}\label{Schw-rad-u0} 1=u^{\mu}u_{\mu}=g_{00}(u^{0})^{2}+g_{11}(u^{1})^{2}= g_{00}(u^0)^{2}(1-\beta^{2})=\gamma^{-2} h (u^0)^{2},\end{equation} thus \begin{equation}\label{Schw-rad-u^mu} u^{\mu}=\gamma\Big( \frac{1}{\sqrt{g_{00}}}, \frac{\beta}{\sqrt{-g_{11}}},0,0\Big)= \gamma\Big(\frac{1}{\sqrt{h}}, \beta\sqrt{h},0,0\Big).\end{equation} For light \[0=k^{\mu}k_{\mu}=g_{00}(k^0)^{2}+g_{11}(k^{1})^{2} \quad\Rightarrow\quad k^{1}=\pm k^{0}\sqrt{-g_{00}/g_{11}}=\pm hk^{0},\] therefor the observer registers (or the detector emits) light with frequency \[\omega_{em}\equiv\omega_{\beta}= g_{\mu}u^{\mu}k^{\nu}= g_{00}u^{0}k^{0}+g_{11}u^{1}k^{1}= h\cdot \frac{\gamma}{\sqrt{h}}k^{0}\pm \frac{1}{h}\cdot\gamma\beta\sqrt{h}\cdot hk^{0}= \sqrt{h}\gamma k^{0}(1\pm\beta).\] Choosing the sign "$+$" here, which corresponds to the emitter moving towards the horizon and light travaling outwards, we obtain the relativistic Dopper effect \begin{equation}\label{RelatDoppler-radial} \omega_{\beta}= \frac{\omega_{0}}{\sqrt{h}}\cdot\gamma(1+\beta)= \omega_{stat}\cdot\gamma(1+\beta).\end{equation} Taking into account that in this case the emitter is moving and detector is at rest, so that $\omega_{em}=\omega_{\beta}$, $\omega_{det}=\omega_{stat}$, we get \begin{equation}\label{Schw-RadialDoppler} \omega_{det}\equiv \omega_{stat}= \omega_{em}\frac{\gamma^{-1}}{1+\beta}= \omega_{em}\sqrt{\frac{1-\beta}{1+\beta}}.\end{equation}
Problem 20: adding the two effects
The source is freely falling the same way, while the detector is stationary at $r_{det}>r_{em}$.
In this case we just need to take into account both the gravitational redshift (\ref{Schw-RedShift}) and the Doppler effect (\ref{Schw-RadialDoppler}). On substituting $\gamma=\sqrt{h_{0}/h_{em}}$, we get \begin{equation}\label{Schw-Rad-FullRedshift} \omega_{det}=\omega_{stat}(r_{em}) \sqrt{\frac{h_{em}}{h_{det}}}= \omega_{em}\frac{\gamma^{-1}}{1+\beta} \sqrt{\frac{h_{em}}{h_{det}}}= \frac{\omega_{em}}{1+\beta}\cdot \frac{h_{em}}{\sqrt{h_{0}h_{det}}}\end{equation} In the limit $r_{em}\equiv r\sim r_{g}\ll r_{det}$ we obtain $\beta\approx 1$, thus \[\omega_{det}\approx \omega_{em}\cdot \frac{h_{em}}{2}= \omega_{em}\cdot {\textstyle\frac{1}{2}} \Big(1-\frac{r_{g}}{r_{em}}\Big)\to 0.\]
Problem 21: intensity
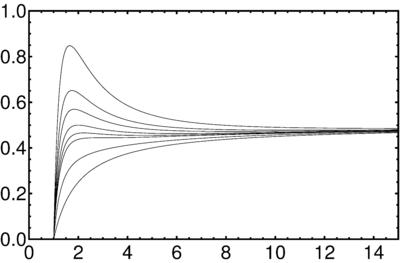
The source is falling freely and emitting continuously photons with constant frequency, the detector is stationary far away from the horizon $r_{det}\gg r_{g}$. How does the detected light's intensity depend on $r_{em}$ at the moment of emission? On the proper time of detector?
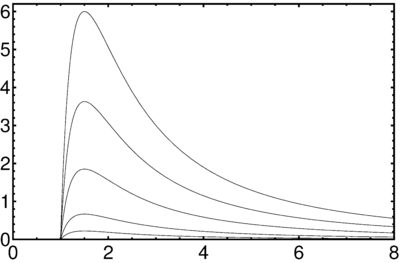
Repeating the argument of this problem, for the proper time interval between detection of consecutive infinitely close signals (\ref{Schw-dtL(dr)}) we have \[dt_{\Lambda}= -\frac{dr}{h}\Big(\frac{1}{v}+\frac{r_{g}}{r}\Big),\] where $dr$ is the corresponding displacement of the emitter, related with its proper time interval as (see \ref{ShwRad-tau}) \[dr=-\gamma v h\, d\tau.\] Then using $\gamma=h^{-1/2}$ from (\ref{SchwRad-V}), we get \begin{equation}\label{Schw-dtL(dTau)} dt_{\Lambda}=\gamma \Big(1+v\frac{r_{g}}{r}\Big) d\tau= h^{-1/2}\Big(1+v\frac{r_{g}}{r}\Big) d\tau.\end{equation} Intensity of the emitted and detected light is proportional to the photons' frequency and inversely proportional to the proper time interval during which a given number $N$ of photons are being emitted/detected. So, combining (\ref{Schw-Rad-FullRedshift}) and (\ref{Schw-dtL(dTau)}), we get \begin{equation}\label{SchwRad-I} \frac{I_{det}}{I_{em}}= \frac{\omega_{det}}{\omega_{em}}\cdot \frac{d\tau}{dt_{\Lambda}}= \frac{1}{1+v} \frac{h_{em}}{\sqrt{h_{0}h_{det}}}\cdot \frac{\sqrt{h_{em}}}{1+v\frac{r_{g}}{r}}.\end{equation} In the limit $h_{0},h_{det}\to 1$ and $r\to r_{g}$, so that $v\to1$, we have \[\frac{I_{det}}{I_{em}}\approx \frac{1}{4}h_{em}^{3/2}= \frac{1}{4}\Big(1-\frac{r_{g}}{r}\Big)^{3/2}.\] Substituting $r(t_\Lambda)$ from (\ref{Schw-r(tL)}), we finally obtain \begin{equation}\label{Schw-I(tL)} I_{det}(t_\Lambda)\approx I_{em}\cdot \exp\Big\{-\frac{3\;t_\Lambda}{4\;r_g}\Big\}.\end{equation}
Orbital motion, effective potential
Due to high symmetry of the Schwarzschild metric, a particle's worldline is completely determined by the normalizing condition $u^{\mu}u_{\mu}=\epsilon$, where $\epsilon=1$ for a massive particle and $\epsilon=0$ for a massless one, plus two conservation laws---of energy and angular momentum.
Problem 22: impact parameter
Show that the ratio of specific energy to specific angular momentum of a particle equals to $r_{g}/b$, where $b$ is the impact parameter at infinity (for unbounded motion).
For $r\gg r_{g}$ we'll have $h\approx 1$ so if we count the angle from $\pi/2$ the impact parameter is $b=r\cos\varphi$. If we denote the length element of the trajectory by $dl$, then the ratio between the angular momentum and energy is \[\frac{L}{E} =\frac{r^2\cdot d\varphi/d\lambda} {h\cdot dt/d\lambda} =\frac{r^2 d\varphi}{hdt}\approx \frac{r^2 (dl\cos\varphi\, /r)}{dl/v}= r\cdot r\cos\varphi=vb.\] In the ultrarelativistic case \[L=Eb.\]
Problem 23: geodesic equations and effective potential
Derive the geodesics' equations; bring the equation for $r(\lambda)$ to the form \[\frac{1}{2}\Big(\frac{dr}{d\lambda}\Big)^{2} +V_{\epsilon}(r)=\varepsilon,\] where $V_{\epsilon}(r)$ is a function conventionally termed as effective potential.
The first equation is $\epsilon=u^{\mu}u_{\mu}$. For a massive particle $\epsilon=1$ and we can also choose the parameter $\lambda$ as the natural parameter of the geodesic $d\lambda=ds$. For a massless particle $\epsilon=0$ and the parameter is arbitrary. In the Schwarzschild metric therefore \begin{equation}\label{Schw-Orbit1} h\Big(\frac{dt}{d\lambda}\Big)^{2}- \frac{1}{h}\Big(\frac{dr}{d\lambda}\Big)^{2}- r^{2}\Big(\frac{d\varphi}{d\lambda}\Big)^{2}= \epsilon.\end{equation} The two integrals of motion (\ref{SchwInt-E1},\ref{SchwInt-L1}) are \begin{equation}\label{Schw-Orbit-Integrals} E=h\frac{dt}{d\lambda};\qquad L=r^{2}\frac{d\varphi}{d\lambda}.\end{equation} Substituting this into (\ref{Schw-Orbit1}) and rearranging terms, we derive the equation for $r(\lambda)$ in the form \begin{equation}\label{Schw-V} \frac{1}{2}\Big(\frac{dr}{d\lambda}\Big)^{2}+ V_{\epsilon}(r)=\varepsilon,\qquad\mbox{where}\quad V(r)=\frac{h}{2} \Big(\epsilon+\frac{L^2}{r^2}\Big), \quad \varepsilon=\frac{E^2}{2}.\end{equation} This is an analogue of one-dimensional motion of a particle in a potential $V$, with the quantity $\varepsilon$ playing the role of full energy (its analytic solution for the given $V$ is expressed through the integral from the square root of a third degree polynomial in the denominator, which is reduced to elliptic Jacobi functions). Note that $V(r=r_{g})=0$. Recall that for massive particles $E$ and $L$ with the chosen parametrization are the energy and angular momentum per unit mass (see (\ref{SchwInt-E2},\ref{SchwInt-L2})).
Problem 24: bound and unbound motion
Plot and investigate the function $V(r)$. Find the radii of circular orbits and analyze their stability; find the regions of parameters $(E,L)$ corresponding to bound and unbound motion, fall into the black hole. Consider the cases of a) massless, b) massive particles.
Let us first consider $\epsilon=0$.
For massless particles the parameter $\lambda$ is arbitrary, so we will fix it by demanding that far from the horizon, where the metric is asymptotically Euclidean, holds $u^{0}\equiv dt/d\lambda=1$. Then, first, $E=1$, and second, at $r\gg r_{g}$ \[0=u^{\mu}u_{\mu}=(u^{0})^{2}-u^{\alpha}u_{\alpha} \quad\Rightarrow\quad \frac{dl}{d\lambda}=1.\] Here $dl$ is the line element of the (asymptotically) flat space, and for such parametrization we obtain that $L=b$, where $b$ is the impact parameter of the ray at infinity: \begin{equation}\label{Schw-orb-NullInts} u^{0}|_{r\to\infty}=1,\;\Rightarrow\quad E=1;\quad L=b.\end{equation} Then \[V_{\epsilon=0}=b^{2}\frac{h}{2r^{2}}= \frac{b^{2}}{2} \Big(\frac{1}{r^2}-\frac{r_{g}}{r^3}\Big), \quad \varepsilon=\frac{1}{2}.\] At small $r/r_{g}$ the effective potential behaves as $\sim (-r^{-3})$, while at large $r/r_{g}$ as $\sim r^{2}$, and reaches its maximum at \[r_{max}=\frac{3}{2}r_{g},\quad V_{max}=V(r_{max})= \frac{2}{27}\Big(\frac{b}{r_g}\Big)^2.\] As this is a maximum, the corresponding circular orbit on the so-called "photon sphere" is unstable. For $\varepsilon>V_{max}$ all the trajectories from one side of it escape to infinity, and the ones from the other side fall on the center (more accurately, they fall on the horizon, as we do not yet consider the motion beyond this point). Rewriting the inequality in terms of $b$, we have \[b<b_{m}\equiv\frac{3\sqrt{3}}{2}\;r_{g}.\] At larger impact parameters there is a "turning point" for motion from infinity, in which $dr/d\lambda=0$. In the region $r<r_{\max}$ these values of $b$, which do not have the meaning of the impact parameter in this case, correspond to finite orbits falling on the center.
For massive particles it is convenient to express $V$ in terms of dimensionless quantities $\xi=r/r_{g}$ and $l=L/r_{g}$: \[V_{\epsilon=1}-\frac{1}{2}=-\frac{1}{2\xi}+ \frac{l^2}{2\xi^2}-\frac{l^2}{2\xi^3}.\] The first term is the Newtonian potential energy, the second one is the centrifugal energy, and only the third term is absent in the Newtonian theory and is unique to General Relativity. It changes the asymptote of $V$ at small $\xi$: $V\sim -\xi^{-3}$ instead of the usual $V\sim\xi^{-2}$.
The extrema of $V$ are found as the roots of quadratic equation \[\xi^2-2l^2 \xi +3l^2=0\quad\Rightarrow\quad \xi_{\pm}=l^{2}\left\{1\pm\sqrt{1-3/l^2}\right\}.\] Two extrema exist, maximum and minimum, if $l>\sqrt{3}$, i.e. $L>L_{cr}$, where \[L_{cr}\equiv\sqrt{12}\,GM.\] The minimum $\xi=\xi_{+}>l^2$ corresponds to a stable circular orbit and non-circular finite motions dangling around it (they are not elliptic). The maximum $\xi=\xi_{-}<l^2$ corresponds to an unstable circular orbit. If $\varepsilon>V(\xi_{-})$, then the motion is infinite with the fall on the center (i.e. at least on the horizon $r=r_g$). The radius of the stable circular orbit is minimal when the discriminant turns to zero: $l=\sqrt{3}$, $\xi_{+}=\xi_{-}=l^{2}=3$, and thus \[r_{circ}^{min}=3r_{g}=6GM.\] For $l<\sqrt{3}$, i.e. $L<L_{cr}$, there are no extrema of $V$ and a particle's motion, either finite ($E<1$) or infinite ($E\geq 1$) always ends with the fall on the center. In the limit $l\gg 1$, which corresponds to $L\gg r_{g}$, \[\xi_{-}\approx3/2,\;\xi_{+}\approx2l^2, \quad\Rightarrow\quad r_{-}=\frac{3}{2}r_{g};\; r_{+}=\frac{2L^{2}}{r_{g}}= \frac{L^2}{GM},\] so the inner unstable orbit tends to the photon sphere, while the outer stable orbit tends to the classical circular one.
Problem 25: gravitational cross-section
Derive the gravitational capture cross-section for a massless particle; the first correction to it for a massive particle ultra-relativistic at infinity. Find the cross-section for a non-relativistic particle to the first order in $v^2/c^2$.
The gravitational capture happens, i.e. a particle moving from infinity falls on the center, if it passes above the effective potential barrier \[\varepsilon\geq V_{\max}.\] (a) For a massless particle we have already found the height of the barrier, so the limiting condition is \[\frac{1}{2}=\frac{2}{27}\Big(\frac{b}{r_g}\Big)^2,\] and for the capture cross-section we get \[S_{\gamma}=\pi b^2 =\frac{27\pi}{4}r_{g}^{2} =27\pi \Big(\frac{GM}{c^2}\Big)^2.\] For a massive particle $V_{\epsilon=1}$ reaches its maximum in the lesser of the two roots $\xi_{\pm}$: \[\xi_{\max}^{-1}=\frac{1}{3}\big(1+\sqrt{1-3/l^2}\big).\] On substituting this into $V(\xi)$, after some transformations we find the maximum: \[V_{\max}=\frac{1}{27}\Big( l^2 +9+\frac{(l^2-3)^{3/2}}{l}\Big).\] (b) Ultrarelativistic case: \[\gamma\gg1,\quad E=\gamma_{\infty}\gg1, \quad\varepsilon =\tfrac{1}{2}\gamma_{\infty}^{2}\gg 1,\] thus $V_{\max}\gg 1$, which only can be when $l\gg1$. In this limit, in the first order by $l^{-2}$ \[V_{\max}=\frac{2}{27}l^2 +\frac{1}{6},\] so the limiting condition of capture is \[l^{2}=\frac{27}{4}\big( \gamma_{\infty}^{2}-\tfrac{1}{3}\big).\] Expressing it through the impact parameter $b=L/Ev$, we are led to \[S_{\gamma\gg1} =\pi b^2=\pi r_{g}^{2}\frac{l^2}{v^2 E^2} =\frac{27\pi}{4}r_{g}^{2}\Big( 1+\frac{2}{3\gamma_{\infty}^{2}}\Big).\] (c) Nonrelativistic case: $E\approx (1+v^2 /2)$, $\varepsilon\approx \tfrac{1}{2}(1+v^2)$, and the limiting condition of capture takes the form \[1+v^2 =\frac{1}{27}\Big( l^2 +9+\frac{(l^2-3)^{3/2}}{l}\Big).\] In the zeroth order by $v^2$ its solution is $l=2$ (note that at $l=\sqrt{3}$ there is no maximum of $V$), while in the first order \[l^2 =4(1+2v^2).\] In terms of impact parameter then the cross-section is \[S_{v\ll 1}=\pi r_{g}^{2}\frac{l^2}{v^2 E^2} \approx \frac{4\pi r_{g}^{2}}{v^2}(1+v^2).\]
Problem 26: innermost stable circular orbit
Find the minimal radius of stable circular orbit and its parameters. What is the maximum gravitational binding energy of a particle in the Schwarzschild spacetime?
The radius of stable circular orbit is minimal when \[\xi_{\min}=l_{min}^{2}=3+0.\] The value of effective potential at $\xi=\xi_{min}$ determines the particle's energy on the corresponding circular orbit (\ref{Schw-V}): \[\frac{E^2}{2}=\varepsilon=V|_{\epsilon=1} =\frac{1}{2}\Big(1-\frac{1}{\xi}\Big) \Big(1+\frac{l^{2}}{\xi^2}\Big)= \frac{1-\xi_{\min}^{-2}}{2},\] where in the last equality we plugged in the value $\xi=\xi_{min}=l_{min}^{2}$. Thus \[E=\sqrt{1-\xi_{min}^{-2}}=\sqrt{\frac{8}{9}} =\frac{2\sqrt{2}}{3}.\] The binding energy then is (in the units of $mc^{2}$) \[1-E=1-\frac{2\sqrt{2}}{3}\approx 0,06.\]
Miscellaneous problems
Problem 27: gravitational lensing
Gravitational lensing is the effect of deflection of a light beam's (photon's) trajectory in the gravitational field. Derive the deflection of a photon's trajectory in Schwarzschild metric in the limit $L/r_{g}\gg 1$. Show that it is twice the value for a massive particle with velocity close to $c$ in the Newtonian theory.
We choose $\lambda$ for massless particles as before and obtain \[\Big(\frac{dr}{d\lambda}\Big)^{2}+ b^{2}\frac{h}{r^2}=1;\qquad \frac{d\varphi}{d\lambda}=b\frac{1}{r^2}.\] Excluding $\lambda$, after integration we obtain $\varphi(r)$. We are interested here in the variation of angle when $r$ goes from infinity to the minimal value, fro which the square root is zero. In the Newtonian theory it is $\pi/2$, so looking for the first correction to this value, we write \[\Delta\varphi\big|_{\pi/2}= b\int\limits_{r_{min}}^{\infty} \frac{dr/r^2} {\sqrt{1-hb^{2}/r^2}}= \left\| x=\frac{b}{r},\;\varepsilon=\frac{r_{g}}{r}\ll 1 \right\|= \int\limits_{0}^{x_{max}} \frac{dx}{\sqrt{1-x^2+\varepsilon x^3}}.\] Changing variables as $x^{2}-\varepsilon x^3=y^2$ and using the small parameter $\varepsilon$, we can transform the integral to one that is easy to compute \[\Delta\varphi\big|_{\pi/2}\approx\int\limits_{0}^{1} \frac{dy}{\sqrt{1-y^2}}(1+\varepsilon y)= \frac{\pi}{2}+\varepsilon= \frac{\pi}{2}+\frac{r_{g}}{b}.\] The second term is the needed correction, which is half the full correction $\delta\phi$ to the angle's variation when a particle moves from infinity and back to infinity: \[\delta\varphi\big|_{\pi}=\frac{2r_{g}}{b}= \frac{4GM}{b c^2}.\] Now let us calculate the same thing in the Newtonian theory for a fast particle. Integrals of motion are \begin{align*} &L=b v_{\infty}=r^{2}\dot{\varphi},\\ &E=U+\frac{\dot{r}^2}{2}+\frac{(r\dot{\varphi})^2}{2} =\frac{\dot{r}^2}{2}-\frac{r_g}{2r}+\frac{L^2}{2r^2}. \end{align*} Then $\varphi(r)$ can be written as \[\varphi=L\int\frac{dr/r^2} {\sqrt{2E+\frac{r_g}{r}-\frac{L^2}{r^2}}},\] and changing variables to $u=r^{-1}$, we obtain for the variation of angle from infinity to the turning point \[\varphi|_{\pi/2}=\int\limits_{0}^{u_{max}}\frac{du} {\sqrt{b^{-2}-u^2+\frac{r_g}{L^2}u}}.\] The last term under the root is a small correction. Let us make another change of variables $u=u'+\varepsilon/2$, where $\varepsilon=r_{g}/L^2 \ll 1$. Then up to terms of higher order by $\varepsilon$ the integral is reduced to \[\varphi|_{\pi/2}=\int\limits_{-\varepsilon/2}^{b^{-1}} \frac{du'}{\sqrt{b^{-2}-{u'}^2}}= \int\limits_{-b\varepsilon/2}^{1} \frac{d\xi}{\sqrt{1-\xi^2}} =\frac{\pi}{2}+\frac{b\varepsilon}{2}.\] Then for motion from infinity to infinity the deflection of the trajectory from a straight line is \[\delta\varphi|_{\pi}=b\varepsilon= \frac{b r_g}{L^2} =\frac{r_g}{b}\frac{1}{v_{\infty}^2} \to \frac{r_g}{b}.\] This is exactly half the correct quantity given by GTR.
Problem 28: generalization of Newtonian potential
Show that the $4$-acceleration of a stationary particle in the Schwarzschild metric can be presented in the form \[a_{\mu}=-\partial_{\mu}\Phi,\quad \text{where}\quad \Phi=\ln \sqrt{g_{00}} =\tfrac{1}{2}\ln g_{00}\] is some generalization of the Newtonian gravitational potential.
For a static particle $u^{\mu}=(u^0,0,0,0)$, where $u^0$ is found from the normalizing condition \[1=u^\mu u_\mu = g_{00}(u^{0})^2\quad \Rightarrow\quad u^{0}=\frac{1}{\sqrt{g_{00}}}.\] Then $4$-acceleration is \[a^\mu=\frac{du^\mu}{ds} =-\Gamma^{\mu}_{\nu\lambda}u^{\nu}u^{\lambda} =-\Gamma^{\mu}_{00}(u^0)^{2}\] and \[a_{\mu}=-\frac{1}{g_{00}}\Gamma_{\mu\,00} =-\frac{1}{2g_{00}}(-\partial_{\mu}g_{00}) =\frac{1}{2}\frac{\partial_{\mu}g_{00}}{g_{00}} =\partial_{\mu}\Phi,\] where $\Phi=\ln\sqrt{g_{00}}$.
Problem 29: coordinate-invariant reformulation
Let us reformulate the problem in a coordinate-independent manner. Suppose we have an arbitrary stationary metric with timelike Killing vector $\xi^\mu$, and we denote the $4$-velocity of a stationary observer by $u^{\mu}=\xi^{\mu}/V$. What is the $4$-force per unit mass that we need to apply to a test particle in order to make it stay stationary? Show in coordinate-independent way that the answer coincides with $\partial_{\mu}\Phi$ (up to the sign), and rewrite $\Phi$ in coordinate-independent form.
From the normalizing condition $V^2=\xi^\mu \xi_\mu$. Here we will use a different meaning of acceleration, natural in the context of GTR. On a geodesic the covariant acceleration of a particle $w^\mu = u^\mu \nabla_{\mu} u^\nu$ is zero; if a particle moves not on a geodesic, this means that some (non-gravitational) force (per unit mass) is acting on it, equal to $w^{\mu}=-a^\mu$. First of all, let us note that, as $\nabla g=0$, \[\xi^{\mu}\nabla_{\mu}V =\xi^{\mu}\xi^{\nu} (\nabla_{\mu}\xi_{\nu}+\nabla_{\nu}\xi_{\mu})=0,\] and also \[2V\nabla_{\mu}V=\nabla_{\mu}V^2 =\nabla_{\mu}\xi^{\nu}\xi_{\nu} =2\xi^{\nu}\nabla_{\mu}\xi_{\nu}.\] Then using stationarity $u^\mu=\xi_\mu /V$ and the Killing equation, we get \[ -a^\mu = w^\mu=\frac{1}{V}\xi^{\nu}\nabla_{\nu} \big(\frac{1}{V}\xi^\mu\big) =\frac{1}{V^2}\xi_{\nu}\nabla^{\nu}\xi^{\mu} =-\frac{1}{V^2}\xi_{\nu}\nabla^{\mu}\xi^{\nu} =-\frac{1}{V}\nabla^{\mu}V=-\nabla^{\mu}\ln V,\] therefore \[a^{\mu}=\nabla^{\mu}\Phi,\quad\text{where} \quad \Phi=\ln V=\tfrac{1}{2}\ln \xi^{\mu}\xi_{\nu}.\] In the weak field limit $g_{00}\approx 1+\tfrac{2\phi}{c^2}$, so $\Phi\approx \phi/c^2$. $\phi$ is the Newtonian gravitational potential.
Problem 30: surface gravity
Surface gravity $\kappa$ of the Schwarzschild horizon can be defined as acceleration of a stationary particle at the horizon, measured in the proper time of a stationary observer at infinity. Find $\kappa$.
The scalar acceleration near the horizon, measured in proper time, is \begin{align*} a=&\sqrt{|a^{\mu}a_{\mu}|} =\sqrt{|g^{\mu\nu}a_{\mu}a_{\nu}|} =\sqrt{|g^{11}|(a_1)^{1}}=\sqrt{|g^{11}|(\Phi')^2}=\\ &=\sqrt{g_{00}}\;\Phi'(r) =\sqrt{g_{00}}\;\frac{g_{00}'}{g_{00}} =\frac{g_{00}'}{2\sqrt{g_{00}}}. \end{align*} It tends to infinity at the horizon. The time of remote observer $t$ is related to the proper time as $dt=d\tau\sqrt{g_{00}}$, therefore acceleration measured in time $t$ is \[a_{\infty}=\sqrt{g_{00}}\;a=\frac{1}{2}g_{00}',\] and it is finite. At $r=r_{g}$ it gives us the surface gravity \[\kappa=a_{\infty}\Big|_{r=r_g}=\frac{1}{2r_{g}} =\frac{c^4}{4MG}.\] In the last equality we restored the dimensional factor $c^2$.
Solving Einstein's equations for a spherically symmetric metric of general form in vacuum (energy-momentum tensor equals to zero), one can reduce the metric to \[ds^2=f(t)\Big(1-\frac{C}{r}\Big)dt^2 -\Big(1-\frac{C}{r}\Big)^{-1}dr^2-r^2 d\Omega^2,\] where $C$ is some integration constant, and $f(t)$ an arbitrary function of time $t$.
Problem 31: uniqueness in exterior region
Suppose all the matter is distributed around the center of symmetry, and its energy-momentum tensor is spherically symmetric, so that the form of $g_{\mu\nu}$ written above is correct. Show that the solution in the exterior region is reduced to the Schwarzschild metric and find the relation between $C$ and the system's mass $M$.
We eliminate the factor $f$ in $g_{00}$ by coordinate transformation $\sqrt{f(t)}dt=dt'$; other components of the metric do not change. In the weak field limit $g_{00}\approx(1+\tfrac{2\varphi}{c^2})$, where $\varphi=-GM/r$ is the Newtonian gravitational potential. Comparing with the asymptote of $g_{00}$ we get \[C=r_{g}=\frac{2GM}{c^2}.\]
Problem 32: solution in a spherically symmetric void
Let there be a spherically symmetric void $r<r_{0}$ in the spherically symmetric matter distribution. Show that spacetime in the void is flat.
The integration constant is determined by the demand of boundedness of $g_{\mu\nu}$ in the region: $C=0$. Then on coordinate transformation $f(t)dt^2=d\tau^2$ we will obtain the flat Minkowskii metric \[ds^2=d\tau^2-dr^2-r^2 d\Omega^2.\]
Problem 33: shells
Let the matter distribution be spherically symmetric and filling regions $r<r_{0}$ and $r_{1}<r<r_{2}$ ($r_{0}<r_{1}$). Can one affirm, that the solution in the layer of empty space $r_{0}<r<r_{1}$ is also the Schwarzschild metric?
With such matter distribution the solution in region $r>r_{2}$ is Schwarzschild, as the constant $C$ and function $f(t)$ are fixed in the usual way. In region $r_{0}<r<r_{1}$, however, we do not have the freedom to choose a new time coordinate, as it will be determined by the smooth sewing-up of the metric at the boundaries (in region $r_{1}<r<r_{2}$ the solution is quite different, of course). Therefore $f(t)\neq 1$ in the inner region.
Problem 34: Einstein equations for spherically symmetric case
Consider a static, spherically symmetric spacetime, described by metric \[ds^{2} =-f(r)dt^{2} +f^{-1} (r)dr^{2} +r^{2} d\Omega ^{2}, \] and write the Einstein's equations for it.
\[(-f)-rf'(r)=-8\pi GPr^{2},\] where $P=T_{r}^{r} $ is the radial pressure of the matter source.
Different coordinates, maximal extension
We saw that a particle's proper time of reaching the singularity is finite. However, the Schwarzschild metric has a (removable) coordinate singularity at $r=r_{g}$. In order to eliminate it and analyze the casual structure of the full solution, it is convenient to use other coordinate frames. Everywhere below we transform the coordinates $r$ and $t$, while leaving the angular part unchanged.
Problem 35: Rindler metric
Make coordinate transformation in the Schwarzschild metric near the horizon $(r-r_{g})\ll r_{g}$ by using physical distance to the horizon as a new radial coordinate instead of $r$, and show that in the new coordinates it reduces near the horizon to the Rindler metric.
The physical distance to the horizon along the "radius" $r$ at $(r-r_{g})\ll r_{g}$ is \[l=\int\limits_{r_{g}}^{r}\frac{dr}{\sqrt{1-r_{g}/r}}= \int\limits_{r_{g}}^{r} \frac{\sqrt{r}dr}{\sqrt{r-r_{g}}}\approx \sqrt{r_{g}}\int\limits_{0}^{r-r_{g}} \frac{d\xi}{\sqrt{\xi}}=2\sqrt{r_{g}(r-r_{g})}.\] Substituting this into the metric, we obtain (restoring the $c$ factors by dimensionality) \[ds^{2}=l^{2}d\omega^{2}-dl^{2}-r^{2}(l)d\Omega^{2}, \qquad\mbox{where}\quad\omega=\frac{ct}{2r_{g}}.\] Comparing with the Rindler metric, we see that $l\equiv\rho=\frac{c^2}{a}$, and $\tau=t\frac{l}{2r_g}$. Thus the static Schwarzschild metric near the horizon has the same form as Minkowskii metric for a uniformly accelerated observer with acceleration $a=\frac{c^2}{l}$, which tends to infinity at the horizon. Then using the inverse transformation, from Rindler to Minkowskii, we can turn the Schwarzschild metric near the horizon into the flat one, thus showing explicitly that $r=r_g$ is just a removable coordinate singularity.
Problem 36: tortoise coordinate
Derive the Schwarzschild metric in coordinates $t$ and $r^\star=r+r_{g}\ln|r-r_g|$. How do the null geodesics falling to the center look like in $(t,r^\star)$? What range of values of $r^\star$ corresponds to the region $r>r_g$?
Making the change of variables $(t,r)\to(t,r^\star)$, we get \[ds^2=\Big(1-\frac{r_g}{r}\Big) \big(dt^2-(dr^\star)^2\big)-r^2 d\Omega^2,\] where $r$ should be understood as a function of $r^\star$. This metric is conformally flat$^{*}$ (without its angular part), and with no singularities. This is achieved, however, by pulling the horizon to infinity: $r=r_g$ corresponds to $r^\star =-\infty$.
$^{*}$A metric $g_{\mu\nu}$ is said to be conformally flat if it differs from the Minkowskii metric $\eta_{\mu\nu}$ by a factor $g_{\mu\nu}=\omega^{2}(x)\eta_{\mu\nu}$.
Problem 37: introducing null coordinates
Rewrite the metric in coordinates $r$ and $u=t-r^\star$, find the equations of null geodesics and the value of $g=det(g_{\mu\nu})$ at $r=r_{g}$. Likewise in coordinates $r$ and $v=t+r^\star$; in coordinates $(u,v)$. The coordinate frames $(v,r)$ and $(u,r)$ are called the ingoing and outgoing Eddington-Finkelstein coordinates.
In different coordinates \begin{align*} ds^2&=\Big(1-\frac{r_g}{r}\Big)dv^2 -\big(dv\,dr+dr\,dv\big)-r^2 d\Omega^2=\\ &=\Big(1-\frac{r_g}{r}\Big)du^2 +\big(du\,dr+dr\,du\big)-r^2 d\Omega^2,\\ &=\frac{1}{2}\Big(1-\frac{r_g}{r}\Big) \big(du\,dv+dv\,du\big)-r^2 d\Omega^2. \end{align*} The null geodesics equations are $v=const$ for the ones falling to the center and $u=const$ for the ones escaping to infinity. Thus, by using the null coordinates $(u,v)$, we rectify the geodesics everywhere including the vicinity of the horizon. In coordinates $(r,v)$ we can analytically extend the solution beyond the horizon. The resulting spacetime region contains all the geodesics corresponding to particles which cross the horizon from the outside in, as well as all the geodesics in the outer region. In coordinates $(r,u)$ we can likewise extend the solution beyond the horizon, and the resulting spacetime will contain, in addition to all the geodesics in the outer region, all the geodesics corresponding to particles crossing the horizon from the inside out. The two considered analytic extensions extend out metric to "different sides". This will be seen better in Kruskal coordinates. In coordinates $(r,u)$ and $(r,v)$ the determinant of $g_{\mu\nu}$ is $g=-r^{4}\sin^{2}\theta$, and in coordninates $(u,v)$ we get $g=-\frac{1}{4}(1-r_{g}/r)^{2}r^{4}\sin^{2}\theta$.
Problem 38: Kruskal-Sekeres metric
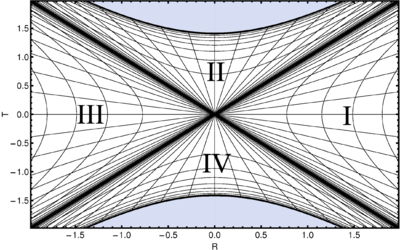
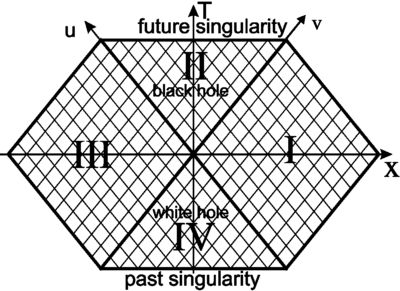
Rewrite the Schwarzschild metric in coordinates $(u',v')$ and in the Kruskal coordinates $(T,R)$ (Kruskal solution), defined as follows: \[v'=e^{v/2r_g},\quad u'=-e^{-u/2r_g};\qquad T=\frac{u'+v'}{2},\quad R=\frac{v'-u'}{2}.\] What are the equations of null geodesics, surfaces $r=const$ and $t=const$, of the horizon $r=r_{g}$, singularity $r=0$, in the coordinates $(T,R)$? What is the range space of $(T,R)$? Which regions in the Schwarzschild coordinates do the regions $\{\text{I}:\;R>|T|\}$, $\{\text{II}:\;T>|R|\}$, $\{\text{III}:\;R<-|T|\}$ and $\{\text{IV}:\;T<-|R|\}$ correspond to? Which of them are casually connected and which are not? What is the geometry of the spacelike slice $T=const$ and how does it evolve with time $T$?
After substitution we obtain \[ds^2=\frac{2r_{g}^3}{r}e^{-r/r_{g}} (dv'\,du'+du'\,dv')-r^{2}d\Omega^2 =\frac{4r_{g}^3}{r}e^{-r/r_{g}} (dT^2-dR^2)-r^{2}d\Omega^2.\] Equations of null geodegics: $u=const$ and $v=const$, or in terms of $(T,R)$: $T=\pm R+const$. The surface $r=const$ is mapped to a hyperbola $T^2-R^2=-2(r-r_g)e^{r/r_g}$; singularity to a hyperbola $T^2-R^2=2r_g$ with two branches also; the horizon to \emph{two} straight lines $T=\pm R$. A surface $t=const$ is mapped to straight line $T=R\tanh\frac{t}{r_g}$; at $t\to\pm\infty$ it coincides with the horizon. Every point $(T,R)$ here represents a two-sphere.
The physical region of values $(R,T)$ is given by condition $r>0$ and the region between the two hyperbola branches $T=\pm\sqrt{2r_g+R^2}$, which represent the past and future singularities. Region I is the asymptotically flat space outside of the horizon (we are living here); region II is the analytical extension along timelike geodesics directed inside across the horizon (coordinates $(r,v)$ map regions I and II); region III is the analytic extension along the timelike geodesics directed away from the horizon (coordinates $(r,u)$ map regions I and III); region IV is \emph{another} asymptotically flat spacetime. It is not casually connected to our spacetime region I. A three-dimensional slice $T=const$ of the entire spacetime for $|T|>\sqrt{2r_g}$ is comprised of two unconnected asymptotically flat regions; for $|T|<\sqrt{2r_g}$ there is a connection between them, the so-called wormhole, or the Einstein-Rosen bridge. This bridge, however, is spacelike: it is seen clearly from the Kruskal diagram that there are no timelike geodesics (or any other timelike curves either) that would correspond to particles coming from one asymptotically flat region into the other.
Problem 39: Penrose diagram
Pass to coordinates \[v''=\arctan\frac{v'}{\sqrt{r_g}},\quad u''=\arctan\frac{u'}{\sqrt{r_g}}\] and draw the spacetime diagram of the Kruskal solution in them.
The coordinates $(v'',u'')$ are needed in order to conformally map the entire Kruskal solution onto a bounded region of parameters $(v'',u'')$, \[|v''|<\frac{\pi}{2},\quad |u''|<\frac{\pi}{2}, \quad |v''+u''|<\frac{\pi}{2}.\] This is a square with two opposite angles cut out, rotated by $\pi/4$. Conformality here means that null geodesics, and thus the casual structure, is left invariant under such transformation, and equations of the null geodesics are still $u''=\pm v'' +const$.
Problem 40: more realistic collapse
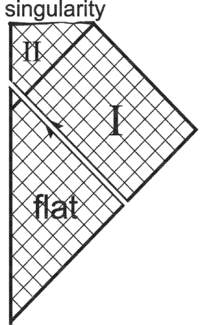
The Kruskal solution describes an eternal black hole. Suppose, for simplicity, that some black hole is formed as a result of radial collapse of a spherically symmetric shell of massless particles. What part of the Kruskal solution will be realized, and what will not be? What is the casual structure of the resulting spacetime?
Outside of the collapsing shell the spacetime should be the Schwarzschild solution. As the particles are massless, their worldlines on the Kruskal diagram lie on the straight line $T-R=const$, and the exterior region contains a part of region I and a part of region II.
The inner region is just a chunk of Minkowskii spacetime, up to the moment of singularity formation. Sewing together of the tho solutions along the spheres of equal circumference $2\pi r$ gives us the full spacetime realized in the considered idealized case of collapse. We see that singularity and horizon are only in the future.