Simple English
A vague definition of a horizon can be accepted as the following: it is a frontier between things observable and things unobservable.
Particle horizon.. If the Universe has a finite age, then light travels only a finite distance in that time and the volume of space from which we can receive information at a given moment of time is limited. The boundary of this volume is called the particle horizon.
Event horizon. The event horizon is the complement of the particle horizon. The event horizon encloses the set of points from which signals sent at a given moment of time will never be received by an observer in the future.
Space-time diagram is a representation of space-time on a two-dimensional plane, with one timelike and one spacelike coordinate. It is typically used for spherically symmetric spacetimes (such as all homogeneous cosmological models), in which angular coordinates are suppressed.
References:[1]
Contents
Problem 1
Draw a space-time diagram that shows behaviour of worldlines of comoving observers in a
- stationary universe with beginning
- expanding universe in comoving coordinates
- expanding universe in proper coordinates
Problem 2
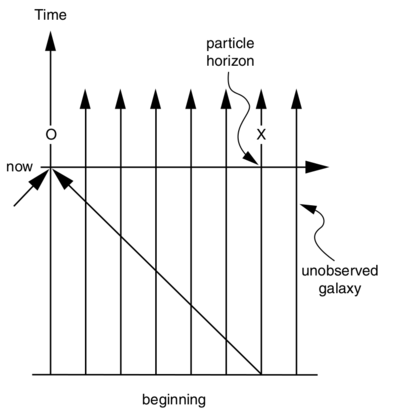
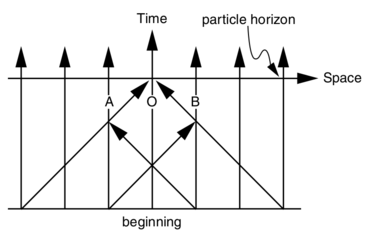
Suppose there is a static universe with homogeneously distributed galaxies, which came into being at some finite moment of time. Draw graphically the particle horizon for some static observer.
The worldline $O$ represents our Galaxy from which we observe the universe. At the present moment we look out in the space and back in time and see other galaxies on our backward lightcone. Worldline $X$ determines the particle horizon. Objects (galaxies) beyond $X$ have not yet been observed by the present moment.
Problem 3
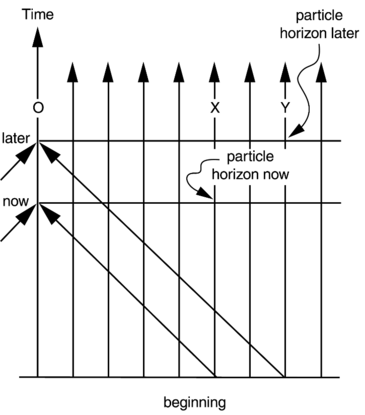
How does the horizon for the given observer change with time?
Problem 4
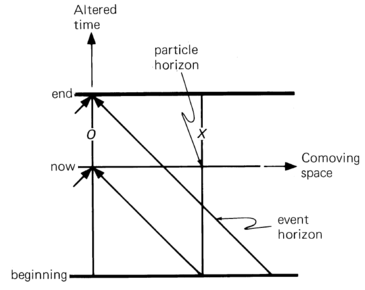
Is there an event horizon in the static Universe? What if the Universe ends at some finite time?
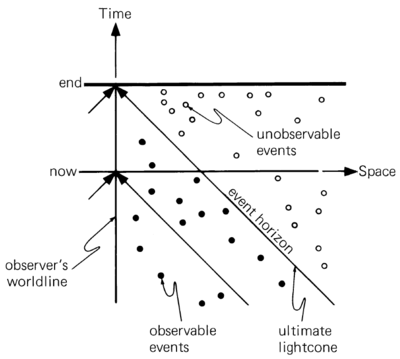
If the Universe is eternal and galaxies shine forever, no event horizons exist. However, it does exist in a Universe that lives for some finite time (has an "end"). For an observer in such a Universe the event horizon is the lightcone built on its worldline at the last possible moment.
Inside this ultimate lightcone are the events that have been seen by the end of the Universe, and outside are the events that can never been seen. The reason is that the lightcone cannot advance farther into time and all events outside of it remain unseen.
Problem 5
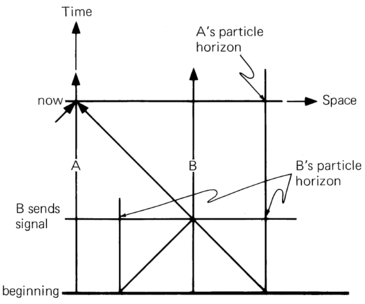
The horizon riddle. Consider two widely separated observers, A and B (see Figure). Suppose they have overlapping horizons, but each can apparently see things that the other cannot. We ask: Can B communicate to A information that extends A's knowledge of things beyond his horizon? If so, then a third observer C may communicate to B information that extends her horizon, which can then be communicated to A. Hence, an unlimited sequence of observers B, C, D, E,... may extend A's knowledge of the Universe to indefinite limits. According to this argument A has no true horizon. This is the horizon riddle. Try to resolve it for the static Universe.
Suppose, for example, that luminous galaxies originated 10 billion years ago and the particle horizon is therefore at distance 10 billion light years. Observers A and B see each other and have overlapping horizons. Suppose A and B are separated by a distance of 6 billion light years (see Figure ). B sends out information that travels at the speed of light and takes 6 billion years to reach A. Hence A receives from B information that was sent 6 billion years ago, when the Universe was 4 billion years old. But B's particle horizon in the past at the time when the information was sent was only 4 billion light years distant. Thus B's horizon at that time did not extend beyond A's present horizon. In other words, B communicates information to A by sending it at the speed of light on A's backward lightcone. But when B sends the information, her horizon extends no farther than A's horizon, and he cannot see farther than A.
Problem 6
Suppose observer O in a stationary universe with beginning sees A in some direction at distance $L$ and B in the opposite direction, also at distance $L$. How large must $L$ be in order for A and B to be unaware of each other's existence at the time when they are seen by O?
Consider two visible bodies at equal distances in opposite directions from us, as shown by world lines A and B on the figure . We see these bodies, but can they see each other? Let $t$ be the time that it takes for light to travel to us from A and B. The time it takes the light to travel from A to B, or from B to A, is obviously $2t$. Hence when the Universe is older than $3t$, we not only see A and B, but they also see each other. If the Universe is younger than $3t$, and older than $t$, we see A and B, but they cannot yet see each other. There is thus a maximum distance beyond which the observed bodies A and B do not know of each other's existence. By examining the spacetime diagram, we see that this maximum distance is one third of the distance to the particle horizon. The answer to our question is that bodies at opposite directions and equal distances from us, which are larger than one third of the distance to the particle horizon, cannot at present see each other.
Problem 7
Draw spacetime diagrams in terms of comoving coordinate and conformal time and determine whether event or particle horizons exist for:
- the universe which has a beginning and an end in conformal time. The closed Friedman universe that begins with Big Bang and ends with Big Crunch belongs to this class.
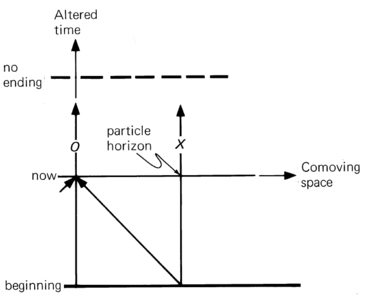
- the universe which has a beginning but no end in conformal time. The Einstein--de Sitter universe and the Friedman universe of negative curvature, which begin with a Big Bang and expand forever, belong to this class.
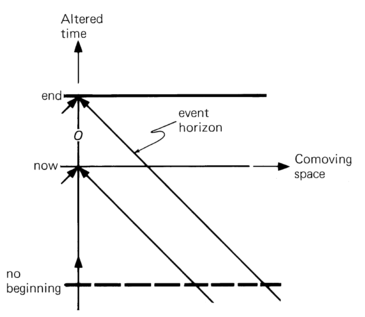
- the universe which has an end but no beginning in conformal time. The de Sitter and steady-state universes belong to this class.
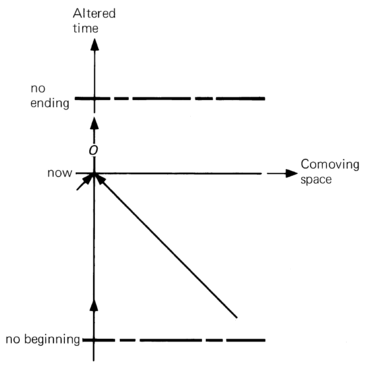
- the universe which has no beginning and no ending in conformal time. The Einstein static and the Milne universes are members of this class.
Conformal time is the altered time coordinate $\eta=\eta (t)$, defined in such a way that lightcones on the spacetime diagram in terms of $\eta$ and comoving spatial coordinate are always straight diagonal lines, even when the universe is not stationary.
- The world line X is at the particle horizon. Notice the existence of an event horizon.
- The particle horizon is at world line X, and no event horizon exists.
- Only the event horizon exists in this case.
- There are no particle or event horizons.
Problem 8
Draw the spacetime diagram in terms of comoving space and ordinary time or the universe with an end but no beginning in conformal time.
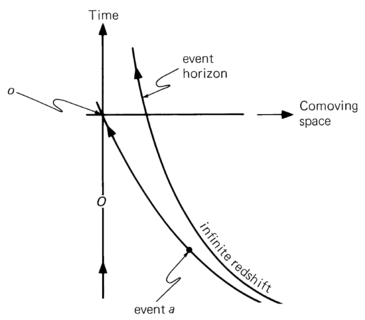
There are universes that expand forever and yet have endings in conformal time. The de Sitter is of this kind and therefore has event horizons. The figure below shows such a universe in a spacetime diagram of comoving space and cosmic time. The event horizon is as shown. As the moment now advances into the infinite future, the observer’s backward lightcone approaches the event horizon more and more closely. For example, the observer O at moment $O$ sees event $a$. As the moment of observation advances into the unlimited future, the lightcone moves upward and approaches more and more slowly but never reaches the event horizon. The event horizon is the observer’s lightcone in the infinite future. Events outside this horizon can never be observed.
Problem 9
Formulate the necessary conditions in terms of conformal time for a universe to provide a comoving observer with
- a particle horizon
- an event horizon
- The necessary condition for the existence of a particle horizon is that conformal time has a beginning (see items I and II of problem 7). The observer's lightcone stretches back and terminates at the lower boundary where the universe begins. When conformal time has no beginning, there is no lower boundary (see items III and IV of problem 7). In this case the lightcone stretches back without limit and intersects all world lines in the universe. In these universes there are no particle horizons. Note that beginning in conformal time does not necessarily mean beginning in ordinary time.
- The necessary condition for the existence of an event horizon is that conformal time has an ending. The event horizon in cosmology is thus nothing more than the observer's ultimate lightcone at the end of conformal time. All the events inside the event horizon (the ultimate lightcone) are at some time observed, and all events outside are never observed. Note that an end in conformal time does not necessarily mean an end in ordinary time.
Problem 10
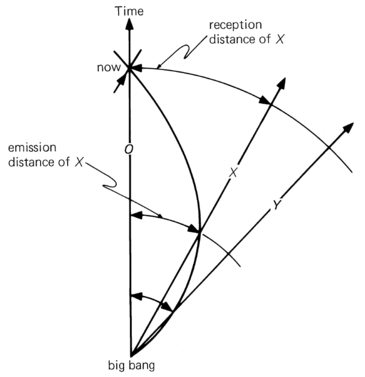
Consider two galaxies, observable at present time, $A$ and $B$. Suppose at the moment of detection of light signals from them (now) the distances to them are such that $L_{det}^{A}<L^{B}_{det}$. In other words, if those galaxies had equal absolute luminosities, the galaxy $B$ would seem to be dimmer. Is it possible for galaxy $B$ (the dimmer one) to be closer to us at the moment of its signal's emission than galaxy $A$ (the brighter one) at the moment of $A$'s signal's emission?
Yes, it is possible. The corresponding spacetime diagram is shown on the figure below . Worldlines branch out radially in all directions from the ``big bang. Spatial slices of constant cosmic time are represented by spherical surfaces perpendicular to the world lines, while time is measured along the radial worldlines. An arbitrary worldline is chosen as the observer and labeled $O$. At some instant in time -- let it be ``now -- the observer's lightcone stretches out and back and intersects other worldlines such as $X$ and $Y$. Because of the expansion of space, the lightcone does not stretch out straight as in a static universe, but contracts back into the big bang. All worldlines and all backward lightcones converge into the big bang.
Problem 11
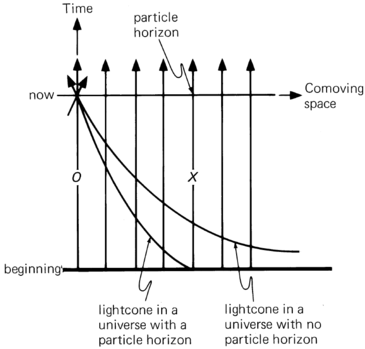
Show on a spacetime diagram the difference in geometry of light cones in universes with and without particle horizons.
A spacetime diagram of comoving space (in which all worldlines are parallel) and cosmic time is shown below . Some universes have particle horizons and in their case the lightcone stretches out and back to the beginning at a finite comoving distance indicated by the world line $X$ . In universes without particle horizons, the lightcone stretches out to an unlimited distance and intersects all world lines.
References
- ↑ E. Harrison. Cosmology: the science of the Universe. CUP (1981)