Solutions of Friedman equations in the Big Bang model

One component dominated Universe

Problem 1: matter or radiation in a flat Universe

Derive $\rho(a)$, $\rho(t)$ and $ a(t)$ for a spatially flat$^*$ ($k=0$) Universe that consists of only

a) radiation,

b) non-relativistic matter$^{**}$.

$^*$ The "spatial" part is often omitted when there cannot be any confusion (and even when there can be), generally and hereatfer.

$^{**}$ In this context and below also quite often called just "matter" or dust.

solution

a) Radiation: $p=\frac{1}{3}\rho$, and from energy conservation \[\dot{\rho}+4\frac{\dot{a}}{a}\rho=0, \quad\Rightarrow\quad \rho\sim \frac{1}{a^{4}}.\] On substitution of this into the first Friedman equation we obtain the equation for $a(t)$ (we use normalization $a_{0}=1$) \[\frac{\dot{a}^{2}}{a^{2}} =\frac{8\pi G}{3}\cdot\frac{\rho_{r0}}{a^4}.\] After integration \[a(t) = \sqrt[4]{\tfrac{32}{3} \pi G{\rho _{r0}}}\;t^{1/2} \quad\mbox{and}\quad \rho_r (t)= \frac 1{\frac {32}{3}\pi G{t^2}}.\] The main result is: \begin{equation}\label{dyn-radiation} \rho_{r}\sim \frac{1}{a^{4}}, \quad a(t) \sim t^{1/2}, \quad \rho_{r}(t)\sim t^{-2}. \end{equation} b) For non-relativistic matter $p=0$, so the energy conservation equation is \[\dot{\rho}+3\frac{\dot{a}}{a}\rho=0, \quad\Rightarrow\quad \rho\sim \frac{1}{a^{3}}.\] In the same way as for the case of radiation domination we get \[a(t) = \sqrt[3]{{6\pi G{\rho _{m0}}}}\;t^{\frac{2}{3}} \quad\mbox{and}\quad \rho_m (t) = \frac{1}{6\pi Gt^2}.\] Then \begin{equation}\label{dyn-matter} \rho_{m}\sim\frac{1}{a^3}, \quad a(t) \sim t^{\frac{2}{3}}, \quad \rho_m (t) \sim t^{-2 }. \end{equation} Note that the dependence $\rho(t)$ is the same in both cases.

Problem 2: RD and MD regimes

Consider two spatially flat Universes. One is filled with radiation (thus radiation dominated, or RD), the other with dust (thus matter dominated, MD). The current energy density is the same. Compare energy densities when both of them are twice as old.

solution

The temporal dependence of energy density in a Universe filled with only one component with equation of state $p=w\rho$ (where $w=const$) can be written as \[\rho(t)=\rho_{0}\frac{t_0^2}{t^2},\] where $\rho_0$ is the current density and \[t_0=\frac{1}{(w+1)\sqrt{6\pi G\rho_0}}\] is the current age of the Universe. When both Universes are twice older, density will be four times smaller in each of them.

Problem 3: RD$\to$MD transition

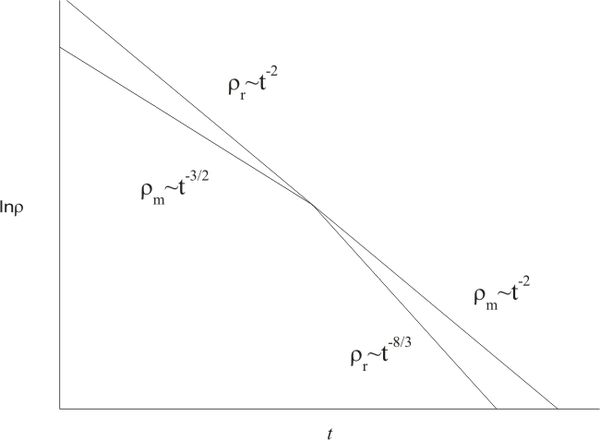
Find the scale factor and density of each component as functions of time in a flat Universe which consists of dust and radiation, for the case one of the components is dominating. Present the results graphically.

solution

• 

  Asymptotic behavior of $\rho(t)$ for the case of background interaction of matter and radiation.

If matter and radiation do not interact, as is assumed, we can write down energy conservation laws for them separately. Then for radiation $\rho_{r}\sim a^{-4}$ and for matter $\rho_{m}\sim a^{-3}$, so energy density of radiation in an expanding Universe always decreases faster than that of non-relativistic matter. Thus the dynamics of the Universe can be divided into two stages: the first one when the dominating component is radiation, and the second one when the dominating component is non-relativistic matter.
The first stage: radiation domination. The first Friedman equation is \[\left(\frac{\dot a}{a}\right)^2 = \frac{8\pi G}{3}(\rho_r + \rho_m)\] When $\rho_r \gg \rho_m$, it takes the form \[\left( \frac{\dot a}{a} \right)^2 \approx\frac{8\pi G}{3}\rho_r.\] Then $a(t)\sim t^{1/2}$ and $\rho_r \sim t^{-2}.$
The dominating component determines the behavior of scale factor as function of time. Therefore we have to plug $a(t)$ for the Universe with dominating radiation into $\rho_m = \rho_m(a)$. Then $\rho_m \sim a^{-3} \sim t^{3/2}$. The relative density of matter increases with time, so the stage of radiation domination is succeeded by the stage of matter domination.
Stage 2: matter domination. Following the same train of thought we get \[ a \sim t^{2/3};\quad\rho _m \sim \frac{1}{t^2}; \quad\rho _r \sim \frac{1}{a^4} \sim \frac{1}{t^{8/3}}.\]

Problem 4: Hubble parameter

Derive the time dependence of the Hubble parameter for a flat Universe in which either matter or radiation is dominating.

solution

a) matter domination $H \equiv\dot a/a = 2/(3t).$
b) radiation domination $H =1/(2t).$

Matter and radiation

Problem 5: exact solutions for matter and radiation

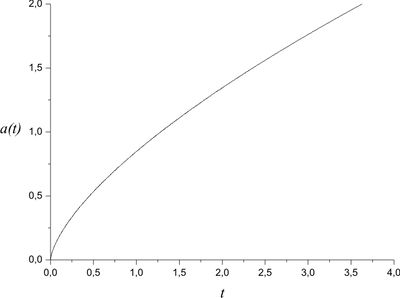
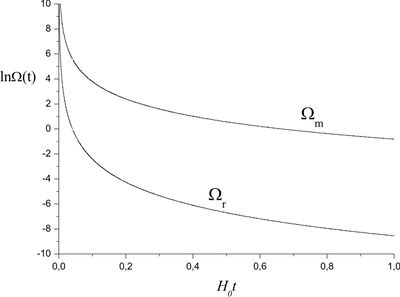
Derive the exact solutions of the Friedman equations for the Universe filled with matter and radiation. Plot the graphs of scale factor and both densities as functions of time.

solution

• 

  Scale factor $a(t)$ for a flat Universe filled with dust and radiation.

• 

  Scale factor $a(t)$ for a flat Universe filled with dust and radiation.

Let us present the total energy density as the sum $\rho=\rho_m+\rho _r$ and plug it into the first Friedman equation \[\left( \frac{\dot a}{a} \right)^2 = \frac{8\pi G}{3}(\rho _r + \rho _m).\] The components' densities $\rho _m$ and $\rho _r$, according to problem, are \[\rho_m=\rho_{m0}\left(\frac{a_0}{a}\right)^{3},\quad \rho _r =\rho_{r0}\left(\frac{a_0}{a}\right)^{4}.\] By definition, $\Omega _i = \rho _i/{\rho _{cr}}$, where \[\rho _{cr} \equiv \frac{3H_0^2}{8\pi G}.\] Then \[\frac{\dot a}{a}= H_0\sqrt{\Omega_{m0}\left(\frac{a_0}{a} \right)^{3} +\Omega _{r0}\left(\frac{a_0}{a} \right)^{4}},\] therefore \begin{equation}\label{dyn-MRgenSol} t = \frac{1}{H_0}\int\limits_{0}^{a/a_0} \frac{dx}{x\sqrt{\Omega_{m0}x^{-3} +\Omega_{r0}x^{ - 4}}} =\frac{1}{H_0}\int\limits_{0}^{a/a_0} \frac{x\,dx}{\sqrt{\Omega_{m0}x +\Omega_{r0}}}. \end{equation}

Problem 6: equipartition time

At what moment after the Big Bang did matter's density exceed that of radiation for the first time?

solution

The condition which determines the time $t_{md}$ when radiation and matter densities became equal is, obviously, $\rho_m=\rho_r$. As $\rho_{m}\sim a^{-3}$ and $\rho_{r}\sim a^{-4}$, then (see problem) \[a_{md} = \frac{\Omega _{r0}}{\Omega _{m0}}a_0.\] Using the results and notation of problem, we get \[t_{md} = \frac{1}{H_0}\int\limits_0^{a_{md}/a_{0}} \frac{x\,dx}{\sqrt {\Omega_{m0}x+ \Omega_{r0}}} =H_{0}^{-1} \frac{\Omega_{r0}^{3/2}}{\Omega_{m0}^{2}} \int\limits_{0}^{1}\frac{y\,dy}{\sqrt{y+1}}=\frac{2(2-\sqrt{2})}{3H_0} \frac{\Omega _{r0}^{3/2}}{\Omega _{m0}^2}.\]

Problem 7: age of the Universe

Determine the age of the Universe in which either matter or radiation has always been dominating.

solution

For the case of matter domination $a\sim t^{2/3}$ (see problem and problem), so $H=\dot{a}/a=2/(3t)$ and \[t_{0}=\frac{2}{3H_{0}}.\] For the case of radiation domination $a\sim t^{1/2}$, $H=\dot{a}/a=1/(2t)$ and \[t_{0}=\frac{1}{2H_{0}}\] Using the observed value $H_0 \approx 7.15\cdot 10^{ - 11}\mbox{yr}^{-1}$, we get $t_0 \approx 9.3 \cdot 10^{9}\mbox{yr}$ for matter and $t_0 \approx 7 \cdot 10^{9}\mbox{yr}$ for radiation.

Non-interacting components, effective potential

Problem 8: constant EoS parameter

Derive the dependence $a(t)$ for a spatially flat Universe that consists of matter with equation of state $p=w\rho$, assuming that the parameter $w$ does not change throughout the evolution.

solution

The energy conservation equation is \[\dot \rho +3 \frac{\dot a}a(1+w)\rho=0.\] On separation of variables and integration with the initial condition $\rho(1)=\rho_0$ (assuming $a_0=1$), we get \begin{equation}\label{dyn-rho(a-w)} \rho(a)=\rho_0a^{-3(1+w)}. \end{equation} Plugging the obtained $\rho(a)$ into the first Friedman equation, we have \[\left( \frac{\dot a}{a} \right)^2 = \frac{8}{3}\pi G\rho_0a^{ - 3(1 + w)}\] and therefore \[a(t) = \left[ \frac{2t}{3(1 + w)} \sqrt {\frac{8}{3}\pi G{\rho _0}} \right]^{\frac{2}{3(1 + w)}},\] thus \begin{equation}\label{dyn-a(t-w)} a(t)=A_{0} t^{\frac{2}{3(1+w)}}. \end{equation}

Problem 9: $H(t)$

Find the Hubble parameter as function of time for the previous problem.

solution

Using the result of the previous problem (\ref{dyn-a(t-w)}) and the definition of the Hubble parameter, we get \[H = \frac{\dot a}{a}= \frac{2}{3\left( {1 + w} \right)t}.\]

Problem 10: effective potential

Using the first Friedman equation, construct the effective potential $V(a)$, which governs the one-dimensional motion of a fictitious particle with coordinate $a(t)$, for the Universe filled with several non-interacting components.

solution

The dynamics of the Universe filled with different components with energy densities $\rho_i$ and equations of state $p_i=w_i\rho_i$ is described by equations \begin{align*} \left( \frac{\dot a}{a} \right)^2 &= \frac{8\pi G}{3} \sum\limits_i \rho _i - \frac{k}{a^2 },\\ \frac{\ddot a}{a} &= - \frac{4\pi G}{3} \sum\limits_i \left(\rho _i + 3p_i \right). \end{align*} Let us use dimensionless variables \[x \equiv \frac{a}{a_0}; \quad \tau \equiv t\left| {H_0 } \right|; \quad \Omega _{i0} \equiv \frac{\rho _{i0}}{\rho _{cr0}}; \quad \rho _{cr0} \equiv \frac{3H_0^2}{8\pi G}; \quad \Omega _{k0}\equiv-\frac{k}{a_0^2 H_0^2}.\] It is assumed that $H_0 \neq 0$. The Friedman equations in terms of new variables are (the dot now denotes derivative by $\tau$) \begin{align*} \frac{1}{2}\dot{x}^2 &=+\frac{1}{2}\sum\limits_i \Omega _{i0} x^{-(1+3w_i)}+\frac{1}{2}\Omega _{k0};\\ \ddot x &=-\frac{1}{2}\sum\limits_i \Omega _{i0} (1 + 3w_i )x^{ - (2 + 3w_i )}. \end{align*} They can be rewritten as \begin{equation}\label{BBpotential1} \frac{1}{2}\dot x^2 + V(x) = E;\qquad \ddot x = - \frac{dV}{dx}, \end{equation} where \begin{equation}\label{BBpotential2} E = \frac{1}{2}\Omega _{k0} ;\qquad V(x) = - \frac{1}{2}\sum\limits_i \Omega _{i0} x^{ - (1 + 3w_i )}. \end{equation}

Problem 11: effective potential for radiation and dust

Construct the effective one-dimensional potential $V(a)$ (using the notation of the previous problem) for the Universe consisting of non-relativistic matter and radiation. Show that motion with $\dot{a}>0$ in such a potential can only be decelerating.

solution

For matter $w_{m}=0$, for radiation $w_{r}=1/3$: \begin{equation}\label{BBpotential3} V(x) = - \frac{\Omega _{m0}}{2x} - \frac{\Omega _{r0}}{2x^2}. \end{equation} We see that $dV/dx>0$ for all $x$, therefore $\ddot{x}=-dV/dx<0$.

Problem 12: exact solutions with dust, radiation and curvature

Derive the exact solutions of the Friedman equations for the Universe with arbitrary curvature, filled with radiation and matter.

solution

Following the consideration of the dynamics of the Universe in terms of an effective potential for variable $a=a/a_{0}$, for the Universe filled with dust ($w=0$) and radiation ($w=1/3$) we use the formulas (\ref{BBpotential1}),(\ref{BBpotential2}), and (\ref{BBpotential3}). Then the solution in quadratures is \[\tau=\int\limits_{0}^{x}\frac{x\,dx} {\sqrt{\Omega_{k0}x^{2}+\Omega_{m0}x+\Omega_{r0}}},\] which can be rewritten as \[t=\sqrt{\frac{a_0}{H_0}}\;\int\limits_{0}^{a/a_0} \frac{x\,dx}{\sqrt{-kx^2+\omega_{m}x+\omega_{r}}},\] where $\omega_{i}=8\pi G a_{0}^{2}\rho_{i0}$.

Deceleration parameter

Problem 13: one component, flat case

Show that for a spatially flat Universe consisting of one component with equation of state $p = w\rho$ the deceleration parameter $q\equiv -\ddot{a}/(aH^2)$ is equal to $\frac{1}{2}(1 + 3w)$.

solution

From the conservation equations \[p = - \frac{\dot \rho }{3H}\frac{w}{1 + w}.\] Then using that \begin{align} w& = \frac{2q - 1}{3}; \\ \dot \rho &= \frac{3}[[:Template:4\pi G]]H\dot H,\quad \dot H = - H^2 (1 + q), \end{align} we find \[p = \frac{H^2}{8\pi G}(2q -1)\]

Problem 14: relation between the total pressure and the deceleration parameter

Find the relation between the total pressure and the deceleration parameter for the flat Universe.

solution

Plugging the first and second Friedman equations into the numerator and denominator correspondingly, we obtain \begin{equation}\label{dyn-q(w)} q = - \frac{\ddot{a}/a}{H^2} = \frac{\frac{4\pi G}{3}\rho(1+3w)} {\frac{8\pi G}{3}\rho}= \frac{1 + 3w}{2}. \end{equation}

Problem 15: $\frac{d^k p}{dt^k }$

The expansion of pressure by the cosmic time is given by \[p(t) = \sum\limits_{k = 0}^\infty {\left. {\frac{1}{k!}\frac{d^k p}{dt^k }} \right|} _{t = t_0 } (t - t_0 )^k. \] Using cosmography parameters (see Chapter 2), evaluate the derivatives $\frac{d^k p}{dt^k }$ up to the fourth order

solution

\begin{align} p& = \frac{H^2 }{8\pi G}(2q - 1);\\ \frac{dp}{dt} &= \frac{H^3 }{4\pi G}(1 - j);\\ \frac{d^2 p}{dt^2} &= \frac{H^4 }{4\pi G}\left( {j - 3q - s - 3} \right);\\ \frac{d^3 p}{dt^3 } &= \frac{H^5 }{4\pi G}\left[ {2s + j - l + q\left( {21 - j} \right) + 6q^2 + 12} \right];\\ \frac{d^4 p}{dt^4 } &= \frac{H^6 }{4\pi G}\big[ j^2 + 3l - m - 144q - 81q^2 - 6q^3 -12j(2 + q) - 3s - 3qs - 60\big]. \end{align}

Problem 16: $w(t)$

Сonsider the universe filled with an ideal fluid with the time-dependent equation of state parameter $w(t)$, and find $\rho (t),H(t)$.

solution

Combination of conservation law and first Friedmann equation gives \[\dot \rho + 2\sqrt {6\pi G} \left[ {1 + w(t)} \right]\rho ^{3/2} = 0\] This equation can be integrated to yield \begin{align} \rho &= \frac{1}{6\pi G\left[ {\int {dt\left( {1 + w(t)} \right)} } \right]^2 }, \\ H(t) &= \frac{2}{3\int {dt\left( {1 + w(t)} \right)} } \end{align} If $w$ is a constant $\left( {w \ne - 1} \right)$, the standard expression for $\rho (t)$ and $H(t)$ is recovered.

Problem 17: $\rho = f(a)$

Find the parameter $w$ in the equation of state if the dependence $\rho = f(a)$ is known. Check the obtained formula for the known special cases.

solution

The conservation equation \[\dot \rho + 3H\rho (1 + w) = 0\] can be rewritten in terms of $\rho = f(a)$ as \[f'(a)\dot a + 3Hf(a)(1 + w) = 0,\] whence we obtain \[w = - \frac{1}{3}\frac{f'(a)}{f(a)}a - 1 = - \frac{1}{3}\frac{d\ln f(a)}{da}a - 1.\]

Problem 18: age of the Universe

Express the age of the spatially flat Universe filled with a single component with equation of state $p=w\rho$ through the deceleration parameter $q=-\ddot{a}/(aH^2)$.

solution

For a spatially flat one-component Universe with equation of state $p=w\rho$, where $w=const$, the scale factor depends on time as (\ref{dyn-a(t-w)}) \[ a(t)\sim t^{2/[3(1+w)]}.\] Then \begin{align*} H=\frac{\dot{a}}{a}&=\frac{2}{3(1+w)}\;\frac{1}{t},\\ \frac{\ddot{a}}{a}&=\frac{2}{3(1+w)} \Big(\frac{2}{3(1+w)}-1\Big)\frac{1}{t^{2}}, \end{align*} and we are immediately led to \[q=\frac{1+3w}{2}=const; \quad t_{0}=\frac{2H_{0}^{-1}}{3(1+w)},\] thus $q$ is constant and \[t_{0}=\frac{H_{0}^{-1}}{1+q}.\]

Problem 19: non-flat generalization

Find the generalization of relation $q = \frac{1}{2}(1 + 3w)$ for the non-flat case.

solution

Excluding the combination $8\pi G$ from the Friedman equations, we get \[\frac{\ddot{a}}{a}= -\frac{1}{2}\left(H^{2}+\frac{k}{a^2}\right)(1+3w),\] therefore \[q = \frac{1+3w}{2} \left(1 + \frac{k}{a^{2}H^{2}}\right).\] We can derive another generalization by simply dividing one of the Friedman equations by the other: \[q=-\frac{\ddot{a}/a}{H^{2}}=\frac{1+3w}{2} \left(1-\frac{k}{a^{2}H^{2}} \frac{\rho_{cr}}{\rho}\right)^{-1}.\]

Problem 20: $q[\rho(a)]$

Show that for a one-component Universe filled with ideal fluid of density $\rho$ \[q=-1-\frac{1}{2}\,\frac{d\ln\rho}{d\ln a}.\]

solution

The energy conservation law can be rewritten as \[a\,d\rho+3da(\rho+p)=0\quad\Leftrightarrow\quad \frac{a}{\rho}\frac{d\rho}{da}=-3(1+w).\] Then plugging $(1+w)$ into the formula for $q$ (\ref{dyn-q(w)}), we obtain \[q=-1-\frac{1}{2}\,\frac{d\ln\rho}{d\ln a}.\]

Problem 21: several components

Show that for a Universe consisting of several components with equations of state $p_{i} = w_{i} \rho_{i}$ the deceleration parameter is \[q = \frac{\Omega }{2} + \frac{3}{2}\sum\limits_i {w_i \Omega_i },\] where $\Omega$ is the total relative density.

solution

Let us write the second Friedman equation for the multi-component model as \[\frac{\ddot a}{a} = \frac{4\pi G}{3}\sum\limits_i ( \rho _i + 3p_i).\] Plugging it into the definition of the deceleration parameter and using $H^2 = 8\pi G\rho_{cr}/3$, we get \[q = - \frac{\ddot aa}{\dot a^2} = \frac{\ddot{a}/a}{H^2} =\frac{\frac{4\pi G}{3}\sum\limits_i ( \rho _i + 3p_i)}{\frac{8\pi G}{3}\rho _{cr}}.\] Then \[q = \frac{\Omega }{2} + \frac{3}{2}\sum\limits_i w_i\Omega _i.\]

Problem 22: acceleration or deceleration

For which values of the state parameter $w$ the rate of expansion of a one-component flat Universe increases with time?

solution

As $\dot{H}=-{H}^{2}(1+q)$, taking into account (\ref{dyn-q(w)}), we obtain \[\dot{H}<0\quad\Leftrightarrow\quad q=\frac{1+3w}{2}<-1\quad\Leftrightarrow\quad w<-1.\]

Closed Universe

Problem 23: closed dusty Universe, exact solution

Show that for a spatially closed ($k=1$) Universe that contains only non-relativistic matter the solution of the Friedman equations can be given in the form \[a(\eta)=a_{\star}(1-\cos\eta); \qquad t(\eta)=a_{\star}(\eta -\sin\eta); \qquad a_{\star}=\frac{4\pi G\rho_0}{3}; \quad 0<\eta<2\pi.\]

solution

Let's use normalization of scale factor by the current value $a_{0}=1$. Taking into account that for matter $\rho\sim a^{-3}$, the first Friedman equation in terms of conformal time $d\eta=dt/a(t)$ is rewritten as \[\frac 1{a^4}\left(\frac{da}{d\eta} \right)^2 =\frac{2a_{\star}}{a^3}-\frac{1}{a^2},\] where \begin{equation}\label{aStar} a_{\star}=\frac{4\pi G \rho_{0}}{3}. \end{equation} After separation of variables and integration, one obtains \[\eta = \int\limits_{0}^{a/a_{\star}} \frac{dx}{\sqrt{2x-x^2}} =-\arccos \Big( 1 - \frac{a}{a_{\star}}\Big).\] Then \begin{align} \label{dyn-closed} a(\eta)&=a_{\star}(1-\cos\eta),\\ t(\eta)=\int a d\eta&=a_{\star}(\eta-\sin\eta), \qquad \eta\in(0,2\pi).\nonumber \end{align} Restoring $a_{0}$ by dimensionality, we get \begin{equation}\label{dyn-closed-dim} \frac{a}{a_0}=\alpha_{\star} (1-\cos\eta),\qquad \frac{t}{a_0}=\alpha_{\star} (\eta-\sin\eta),\qquad \alpha_{\star}=a_{0}^{2}a_{\star} =\frac{4\pi G}{3}\rho_{0}a_{0}^{2}. \end{equation}

Problem 24: size and lifetime

Find the relation between the maximum size and the total lifetime of a closed Universe filled with dust.

solution

We make use of the exact solution in the form (\ref{dyn-closed}). As the range of values of $\eta$ is $[0,2\pi]$, the total lifetime is $T=2\pi a_{\star}$, while the maximal size is reached at $\eta=\pi$: $a_{\max}=2a_{\star}$. Then \[T=\pi a_{\max}.\]

Problem 25: future through observables

Suppose we know the current values of the Hubble constant $H_0$ and the deceleration parameter $q_0$ for a closed Universe filled with dust only. How many times larger will it ever become?

solution

The current value of $a_0$ can be expressed through the observed quantities using the definition of the deceleration parameter $q$: \begin{equation}\label{dyn-a0} q=-\frac{\ddot{a}/a}{H^2} =\frac{\frac{4\pi G}{3}\rho}{H^2} =\frac{1}{2}\Big(1+\frac{1}{a^2 H^2}\Big), \quad\Rightarrow\quad a_0^2 H_0^2=\frac{1}{2q_0 - 1}. \end{equation} Then \[\alpha_{\star}=\frac{4\pi G }{3} \cdot \rho_0 a_{0}^{2} =\frac{a_{0}^{2}}{2} \Big(H_{0}^{2}+\frac{1}{a_{0}^{2}}\Big) =\frac{a_{0}^{2}H_{0}^{2}+1}{2} =\frac{q_0}{2q_0 -1}.\] The scale factor reaches its maximum at $\eta=\pi$ and \begin{equation}\label{dyn-alphaStar} \frac{a_{\max}}{a_0} =2\alpha_{\star}=\frac{1}{1-1/2q_{0}}. \end{equation} Then the maximal value of the size of the Universe can be written as \begin{equation}\label{dyn-Amax} a_{\max}=H_{0}^{-1}\frac{2q_{0}}{(2q_0 -1)^{3/2}}. \end{equation}

Problem 26: age of the Universe

In a closed Universe filled with non-relativistic matter the current values of the Hubble constant is $H_0$, the deceleration parameter is $q_0$. Find the current age of this Universe.

solution

From the general solution (\ref{dyn-closed-dim}) \[t_{0}=a_{0}\alpha_{\star}(\eta_0 - \sin\eta_0),\] where, taking into account (\ref{dyn-alphaStar}), \[\eta_{0}=-\arccos(1-\alpha_\star^{-1}) =-\arccos(q_{0}^{-1}-1).\] On substitution of $a_0$ from (\ref{dyn-a0}), we get \[t_{0}=\frac{H_{0}^{-1}}{2q_0 -1}\Big( 1+\frac{q_0}{\sqrt{2q_0 -1}} \arccos(q_{0}^{-1}-1)\Big).\]

Problem 27: around the Universe

Suppose in the same Universe radiation is dominating during a negligibly small fraction of total time of evolution. How many times will a photon travel around the Universe during the time from its "birth" to its "death"?

solution

First of all, note, that in a stationary closed Universe a photon (as any other particle) that is emitted from a given point in arbitrary direction, travels "around the world" in finite time and returns to the initial point from the opposite direction, very much like a particle moving in a "straight line" on a two-dimensional sphere does. The trigonometric radial coordinate $\chi$, such that $d{\chi ^2} = d{r^2}/(1 - {r^2})$ (see problem of chapter 2), changes during the round-trip from $0$ to $\pi$ (on the opposite pole) and back to zero. In terms of conformal time $d\eta / a(t)$ and $\chi$ the interval for a radially propagating photon $(d\theta = d\varphi = 0)$ is \[d{s^2} = a{(t)^2}(d{\eta ^2} - d{\chi ^2})=0,\] We know (see problem) that the lifetime of the Universe, i.e. the interval between two zeros of $a(\eta)$ corresponds to the interval $\Delta\eta=2\pi$. During this time a photon will travel distance $\Delta\chi=2\pi$, thus making exactly one round-trip around the Universe.

Problem 28: different volumes in dynamical Universe

In a closed Universe filled with dust the current value of the Hubble constant is $H_0$ and of the deceleration parameter $q_0$.

a) What is the total proper volume of the Universe at present time?

b) What is the total current proper volume of space occupied by matter which we are presently observing?

c) What is the total proper volume of space which we are directly observing?

solution

a) The volume of a closed Universe with scale factor $a_0$ was found in problem: $V_{0}=2\pi^2 a_{0}^{3}$. Using the expression for $a_{0}$ through the measured quantities $H_0$ and $q_0$ (\ref{dyn-a0}), we get then \[V_0 = 2\pi^2a_0^3 = 2\pi^2 H_0^{-3}(2q_0-1)^{-3/2}.\] b) The spatial metric of the closed Universe is \[dl^{2}=a^{2}\big(d\chi^2 +\sin^{2}\!\chi\; d\Omega^{2}\big), \quad d\Omega^{2}=d\theta^2 +\sin^{2}\theta d\varphi^2,\] so the volume element between spherical layers of "radii" $\chi$ and $\chi+d\chi$ is \[dV_{\chi}=4\pi\cdot a^{2}\sin^{2}\chi \cdot a\,d\chi =4\pi a^{3}\sin^{2}\chi d\chi.\] At present we have received light emitted with the radial comoving coordinate $\chi$ equal to at most the conformal age of the Universe \[\eta_{0}=-\arccos(1-\alpha_{\star}^{-1}) =-\arccos(q_{0}^{-1}-1),\] where in the second equality sign we used (\ref{dyn-alphaStar}) . Then \begin{align*} V_{b}=4\pi a_{0}^{3} \int\limits_{0}^{\eta_0}d\eta \sin^{2}\eta \end{align*} Assuming here $\eta_{0}=\pi$, which corresponds to the moment of maximal expansion, we obtain the total volume of the Universe calculated in problem at this same moment. At later times $\eta>\pi$ we can see all of the Universe, moreover some points from different directions, so the formula is not applicable. c) The volume that we are observing directly differs from the calculated above as we see the distances between objects as they were at the moment of emission, not as they are "now", so one $a(t)$ shoulf be left inside the integral. Otherwise following the same steps, we arrive to \[V_{c}=4\pi (a_{0}\alpha_{\star})^{3} \int\limits_{0}^{\eta_{0}}d\eta\, (1-\cos\eta)^{3}\sin^{2}\eta.\] In more rigorous terms: consider the $4$-volume $\Omega$ filled with worldlines of all particles which we are currently observing (i.e. the ones the light from which took less time to arrive to us than the age of the Universe). The previous volume $V_{b}$ was the spatial volume that the observed matter occupies "at present", i.e. it is the volume of the section $t=t_{0}$ of $\Omega$. The volume $V_{c}$ is the 3-volume of the section of $\Omega$ by the light "cone" directed to the past with the vertex at the observer (it is actually a cone only in Minkowski spacetime, and is quite deformed for Friedmannian spaces).

Different problems

Problem 29: open dusty Universe

Find the solution of Friedman equations for spatially open ($k=-1$) Universe filled with dust in the parametric form $a(\eta)$, $t(\eta)$.

solution

The solution differs from the one for $k=+1$ (problem) only by the sign of $k$. Likewise the first Friedman equation is rewritten as \[\frac 1{a^4}\left(\frac{da}{d\eta} \right)^2 =\frac{2a_{\star}}{a^3}+\frac{1}{a^2}, \quad\text{where}\quad a_{\star}=\frac{8\pi G \rho_{0}}{3},\] and on integration we obtain \[ \eta=\int\limits_{0}^{a/a_{\star}} \frac{dx}{\sqrt{2x+x^{2}}} =\text{arcosh}\Big(1+\frac{a}{a^{\star}}\Big),\] so trigonometric functions are replaced by the hyperbolic ones and \begin{align}\label{dyn-open} a(\eta)&=a^{\star}(\cosh\eta-1),\\ t(\eta)=\int a d\eta&=a^{\star}(\sinh\eta-\eta), \qquad \eta\in(0,\infty).\nonumber \end{align}

Problem 30: density evolution

Suppose the density of some component in a spatially flat Universe depends on scale factor as $\rho(t) \sim a^{-n}(t)$. How much time is needed for the density of this component to change from $\rho_1$ to $\rho_2$?

solution

Let $\rho(t) = b a(t)^{-n}$, then expressing $a$ and $\dot{a}$ in the first Friedman equation through $\rho$ and $\dot{\rho}$, we are led in result to equation \[\frac{d\rho}{dt}=n\sqrt{ \frac{8\pi G}{3}}\rho^{3/2},\] and after integration to \[ \Delta t =\frac{1}{n} \sqrt{\frac{3}{8\pi G}} \int\limits_{\rho_1}^{\rho_2}\!d\rho\;\rho^{-3/2} =\frac{2}{n}\sqrt{ \frac{3}{8\pi G}}\;\; \big(\sqrt{\rho_1}-\sqrt{\rho_2}\big).\]

Problem 31: $q[H(t)]$

Using the expression for $H(t)$, calculate the deceleration parameter for the cases of domination of

a) radiation,

b) matter.

solution

As \[\frac{d}{dt}\frac{1}{H}=\frac{d}{dt}\frac{a}{\dot{a}} =1-\frac{a\ddot{a}}{a^2}=1+q,\] from \[H=\frac{2}{3(1+w)t}\] we obtain the formula already derived above (\ref{dyn-q(w)}) \[q=\frac{3(1+w)}{2}-1=\frac{1+3w}{2}.\] Then a) for radiation $q=\frac{1}{2}$; b) for matter $q=1$.

Problem 32: effective EoS for multi-component Universe

Consider a Universe consisting of $n$ components, with equations of state $p_{i}=w_{i}\rho_{i}$, and find $w_{tot}$, the parameter of the equation of state $p_{tot}=w_{tot}\rho_{tot}$.

solution

By definition \[p_{tot}=w_{tot}\rho_{tot},\] so \begin{equation}\label{w_tot_i} w_{tot}=\frac{\sum\limits_i w_i \rho_i}{\sum\limits_i \rho_i}=\frac{\sum\limits_i w_i \Omega_i}{\sum\limits_i \Omega_i}. \end{equation} For a flat Universe $\sum\Omega_{i}=\Omega=1$, and in case of two-component medium \begin{equation}\label{w_tot_d_m} w_{tot}=\Omega_{m}w_{m}+\Omega_{d}w_{d}. \end{equation}

Problem 33: relative densities

Derive the equations of motion for relative densities $\Omega_{i}=\rho_{i}/\rho_{cr}$ of the two components comprising a spatially flat two-component Universe, if their equations of state are $p=w_i\rho$, $i=1,2$.

solution

First let us note that from the conservation laws for each of the components separately and both of them together \begin{align*} \dot{\rho}_{i}&=-3H(1+w_{i})\rho_{i};\\ \dot{\rho}_{tot}&=-3H(1+w_{tot})\rho_{tot}. \end{align*} On substitution of $\dot{\rho}_{i}$ into the time derivative of $\Omega_{i}=\rho_{i}/\rho_{cr}$ we get \[\frac{1}{H}\dot{\Omega}_{i}=\frac{1}{H} \frac{\dot{\rho}_{i}\rho_{tot}- \rho_{i}\dot{\rho}_{tot}}{\rho_{tot}^{2}} =3\Omega_{i}(w_{tot}-w_{i}).\] For a two-component flat Universe we can use the result (\ref{w_tot_d_m}) for $w_{tot}$, thus \[\dot{\Omega}_{m}=-\dot{\Omega}_{r} =3H\Omega_{m}\Omega_{r}(w_{r}-w_{m}).\]

Problem 34: EoS for non-relativistic gas

Suppose a Universe is initially filled with a gas of non-relativistic particles of mass density $\rho_{0}$, pressure $p_{0}$, and $c_p/c_v=\gamma$. Construct the equation of state for such a system.

solution

Let us rewrite the conservation law in the Friedmannian Universe \[\dot{\rho}+3H(\rho+p)=0\] (here $c=1$) in the form \[\dot{\rho}+\frac{\dot{V}}{V}(\rho+p)=0,\] and passing to differentiation by pressure $p$ instead of time $t$, as \[\frac{d\rho}{dp}+\frac{1}{V}\frac{dV}{dp} (\rho+p)=0.\] For adiabatic expansion \[pV^\gamma = const\quad \Rightarrow\quad V\sim p^{-1/\gamma}\quad \Rightarrow\quad \frac{1}{V}\frac{dV}{dp}=-\frac{1}{\gamma p}.\] Plugging this into the conservation law, we get a differential equation for $\rho(p)$: \[\gamma p\cdot \rho'=\rho+p.\] Its solution is %\[\rho=\rho _m + \frac{p}{\gamma-1}.\] \[\rho(p)=\frac{p}{\gamma-1}+C\,p^{1/\gamma}.\] Using the initial conditions then \[\rho(p)=\frac{p}{\gamma-1} +\Big(\rho_{0}-\frac{p_{0}}{\gamma-1}\Big) \left(\frac{p}{p_{0}}\right)^{1/\gamma}.\]

Problem 35: Newtonian derivation of critical density

Derive the expression for the critical density $\rho_{cr}$ from the condition that Hubble's expansion velocity equals the second cosmic velocity (escape velocity) $v=\sqrt{2gR}$.

solution

Let us consider the spherical region of radius $R$ with density $\rho_{cr}$. Putting down the escape velocity as $\dot R$, we obtain \[\dot R^2 = 2\frac{G\rho _{cr}\cdot\frac{4}{3}\pi R^3}{R^2}R.\] Then taking into account the definition of $H = \dot R/R$, \[\rho_{cr}=\frac{3H^2}{8\pi G}.\]

X-component

Problem 36: dust plus something else

Suppose the Universe is filled with non-relativistic matter and some substance with equation of state $p_X=w\rho_X$. Find the evolution equation for the quantity $r \equiv \frac{\rho_m}{\rho _X}$.

solution

From $r=\rho_{m}/\rho_{X}$ \[\dot r = \frac{{\dot \rho}_m}{\rho _X} - {\dot \rho }_X{\rho_m}{\rho _X^2}.\] Then on substitution of ${\rho _m}$ and ${\rho _X}$ from the corresponding conservation laws, we get \[\dot r = 3Hwr.\]

Problem 37: deceleration parameter

Express the deceleration parameter through the ratio $r$ for the conditions of the previous problem.

solution

Similarly to problem, on substitution of the right hand parts of the Friedman equations into the numerator and denominator, we get \[q = - \frac{\ddot{a}/a}{H^2} = \frac{\frac{4\pi G}{3}(\rho + 3p)}{\frac{8\pi G}{3}\rho } = \frac{1}{2}\frac{\rho_m + \rho_X + 3w\rho _X}{\rho_m +\rho _X} =\frac{1}{2} + \frac{3w}{2(1+r)}.\] Another way: \[q = - 1 + \frac{d}{dt}\left( \frac{1}{H} \right) = - 1 - \frac{\dot H}{H^2};\] \[\dot H = - 4\pi G(\rho + p), \quad {H^2} = \frac{8\pi G}{3}\rho.\]

Problem 38: $\rho_{X}\propto H^2$

Let a spatially flat Universe be filled with non-relativistic dust and a substance with equation of state $p_{X}= w\rho_{X}$. Show that in case $\rho_{X}\propto H^2$, the ratio $r =\rho_{m}/\rho_{X}$ does not depend on time.

solution

The Friedman equations can be written as \[3{H^2} = 8\pi \rho - 3\frac{k}{a^2},\] \[\dot H = - 4\pi G\left( {\rho + p} \right) + \frac{k}{a^2}.\] Then \[2\frac{{\dot{H}}}{H} =-3H\left( 1+\frac{p}{\rho } \right) -\frac{k}{{{a}^{2}}H}\left( 1+3\frac{p}{\rho } \right).\] Combining this with the conservation equation for $\rho_X$, we get \[\frac{\dot{\rho}_X}{\rho_X} -2\frac{\dot{H}}{H} =-\frac{3Hwr}{1+r}+\frac{k}{{{a}^{2}}H} \left( 1+3\frac{w}{1+r} \right)\] In the considered case (see problem) $\dot{r}=3Hwr$, so we arrive to \[\dot{r}=-\left( 1+r \right)\left[ \frac{{{{\dot{\rho }}}_{X}}}{{{\rho }_{X}}}-2\frac{{\dot{H}}}{H}-\frac{k}{{{a}^{2}}H}\left( 1+3\frac{w}{1+r} \right) \right].\] If ${{\rho }_{X}}\propto {{H}^{2}}$, then \[\dot{r}=(1+r) \frac{k}{{{a}^{2}}H}\left( 1+3\frac{w}{1+r} \right).\] Thus we obtain immediately that for a flat Universe $\dot{r}=0$.

Problem 39: $r(q)$

Show that for the model of the Universe described in the previous problem the parameter $r$ is related with the deceleration parameter as \[\dot{r}=-2H\frac{\Omega_{curv}}{\Omega_X}q.\]

solution

Combining \[\dot{r}=(1+r)\frac{k}{{{a}^{2}}H}\left( 1+3\frac{w}{1+r} \right)\] with \[q=\frac{1}{2}\left( 1+\frac{k}{{{a}^{2}}{{H}^{2}}} \right)\left( 1+3\frac{w}{1+r} \right)\] we find \[\dot{r}=2\left( 1+r \right)\frac{k}{{{a}^{2}}H}\frac{q}{1+\frac{k}{{{a}^{2}}{{H}^{2}}}}\] Using the relative densities \[{{\Omega }_{m}}=\frac{8\pi G}{3{{H}^{2}}}{{\rho }_{m}},\quad {{\Omega }_{X}}=\frac{8\pi G}{3{{H}^{2}}}{{\rho }_{X}},\quad {{\Omega }_{curv}}=-\frac{k}{{{a}^{2}}{{H}^{2}}}\] we can transform the combination $1+r$ to \[1+r=1+\frac{{{\rho }_{m}}}{{{\rho }_{X}}}=\frac{1-{{\Omega }_{curv}}}{{{\Omega }_{X}}}=\left( 1+\frac{k}{{{a}^{2}}{{H}^{2}}} \right)\frac{1}{{{\Omega }_{X}}}\] Finally \[\dot{r}=-2H\frac{{{\Omega }_{curv}}}{{{\Omega }_{X}}}q\] Yet again we confirm that for the considered model in the flat case $\dot{r}=0$.

Problem 40: $r$ in open and closed cases

Show that in the model of the Universe of problem, in case $k=+1$ and $q>0$ (decelerated expansion) $r$ increases with time, in case $k=+1$ and $q<0$ (accelerated expansion) $r$ decreases with time, and for $k=-1$ vice-versa.

solution

The result immediately follows from the ralation obtained in the previous problem \[\dot{r}=-2H\frac{{{\Omega }_{curv}}} {{{\Omega }_{X}}}q\] and definition \[{\Omega }_{curv}=-\frac{k}{{{a}^{2}}{{H}^{2}}}.\]

Power-law cosmology

The following problems on power-law cosmology are inspired by Kumar [1].

Problem 41: power-law cosmologies

Let us consider a general class of power-law cosmologies described by the scale factor \[a(t) =a_{0}\Big(\frac{t}{t_0}\Big)^\alpha,\] where $t_0$ is the present age of theUniverse and $\alpha$ is a dimensionless positive parameter. Show that:

1) the scale factor in terms of the deceleration parameter may be written as \[a(t) =a_{0}\Big(\frac{t}{t_0}\Big)^{1/1 + q}, \quad\text{i.e.}\quad \alpha=\frac{1}{1+q}.\]

2) the expansion of the Universe is described by Hubble parameter \[H=\frac{1}{(1+q)\;t}\] or in terms of redshift \[H(z)=H_{0}(1+z)^{1+q}.\]

solution

As $H=\dot{a}/a=\alpha/t$, using the definition for the deceleration parameter, we get \[q=-\frac{\ddot{a}/a}{H^2}=\frac{1-\alpha}{\alpha},\] so \[\alpha=\frac{1}{1+q},\qquad H=\frac{1}{(1+q)\;t}.\]

Problem 42: age of the Universe

In the power-law cosmology find the age of the Universe at redshift $z$.

solution

In the general case, using the relation $(1+z)=1/a$, we can relate the age of the Universe to the expansion history as \[t=\int dt=\int \frac{da/a}{H} =\int\limits_{z}^{\infty} \frac{dz}{(1+z)H}.\] Then using the result of the previous problem), on integration we find \[t(z)=\frac{\alpha/H_{0}}{(1+z)^{1/\alpha}}.\]

Problem 43: luminosity distance

For the power-law cosmology find the luminosity distance between the observer and the object with redshift $z$.

solution

The luminosity distance is \[{D_L}(z) = (1 + z)\int_0^z \frac{dz'}{H(z')} = \frac{1 + z}{H_0}\frac{\alpha }{1-\alpha} (1 + z)^{\frac{\alpha-1}{\alpha}}\Big|_{0}^{z} =\frac{H_{0}^{-1}}{q} (1+z)\big[1-(1+z)^{1-q}\big].\]

Problem 44: a "softer" version of the cosmological evolution

The power law cosmological evolution $a(t)\propto t^{\beta }$ leads to the Hubble parameter $H(t)\propto 1/t$. Consider a "softer" version of the cosmological evolution given by the law \[H(t)=\frac{S}{t^{\alpha } } \] where $S$ is a positive constant and $0<\alpha <1$. Analyze the dynamics of such model at $t\to 0$.
(F.Cannata, A.Kamenshchik, D.Regoli, arXiv:0801.2348).

solution

Integrating $\frac{d}{dt} \left(\ln a\right)=\frac{S}{t^{\alpha } } $ we obtain \[\ln \left(\frac{a(t)}{a(0)} \right)=\frac{S}{1-\alpha } t^{1-\alpha } \] At $t=0$ singularity is present, but it is different from the traditional Big Bang singularity. If $t\ne 0\, (t>0)$, the right hand side is finite and hence one cannot have $a\left(0\right)=0$ in the left hand side. Then $a(0)>0$, while \[\dot{a}(t)=a(0)\frac{S}{t^{\alpha } } \exp \left(\frac{S}{1-\alpha } t^{1-\alpha } \right)\mathop{\to }\limits_{t\to 0} \, \infty. \] This type of singularity received the name of "soft Big Bang singularity" because the cosmological scale factor is finite (and non-zero) while its time derivative, the Hubble variable and the scalar curvature are singular. It is interesting to note that when $t\to \infty $ both $a(t)$ and $\dot{a}(t)$ tend to infinity, but they do not encounter any cosmological singularity because the Hubble variable and its derivatives tend to zero.