ANONIMOUS
Problem 1
Find the lower limit for the mass of the dark matter particles in case they are:
a) bosons;
b) fermions.
If the dark matter consists of bosons then the de Broglie wavelength of the particles must be shorter than the galactic size ($\sim 1 \mbox{ kpc}$). For typical velocities $v\sim 250${ km/s}, one obtains $m \leq 10^{-22} \mbox{ eV}$. This inequality does not pose any restriction on mass of the boson as a candidate for the dark matter particle.
Problem 2
Find the lower limit for the mass of fermion particles that constitute a compact spherical object of dark matter with radius $R$ and mass $M$.
The bound $m_{lb}$ can be determined from the condition that maximum speed of degenerated fermi gas with gravitational interaction does not exceed the escape velocity: $v_\infty = \left(2GM/R\right)^{1/2} $ : \[\hbar \left( {\frac{9\pi M}{2gm^4 R^3 }} \right) \le \sqrt {\frac{2GM}{R}} \Rightarrow m \ge m_{lb} = \left( \frac{9\pi \hbar ^3 }{4\sqrt 2gM^{1/2} R^{3/2} G^{3/2}}\right)^{1/4}. \] Here $g$ is the number of internal degrees of freedom for the dark matter particles.
Problem 3
Show that particles that contitute a galaxy of mass $M=10^{10}M_\odot$ and radius $R=3kpc$ must be non-relativistic.
Escape velocity $v_\infty$ for particles in the galaxy can be found from the condition \[ \frac{mv_\infty ^2 }{2} = G\frac{mM}{R} \Rightarrow v_\infty = \sqrt {\frac{2GM}{R}} \approx 10^5 \mbox{ m/s} \] As the particle velocities in the galaxies cannot exceed the escape velocity $v < v_\infty $, then the particles must be non-relativistic.
Problem 4
In assumption that neutrinos have mass $m_\nu$ and temperature of decoupling $T_D\simeq1MeV$, determine their contribution to the presently observed energy density.
$\Omega_\nu h^2 = {m_\nu}/{91.5\mbox{eV}}$.
If WIMPs represent dark matter, they will not just generate the background density of Universe, but they will also cluster together with the usual baryon matter in the galactic halo. In particular, they will be presented in our own galaxy - the Milky Way. It gives hope to detect the relic WIMPs immediately on the Earth. What is these hope related to? By definition, WIMPs do not interact with photons. However, WIMPs could annihilate into usual matter (quarks and leptons) in the early Universe. Otherwise they would have too high relative abundance today. Due to the crossover symmetry, the temperature of annihilation of e.g. WIMPs into quarks is related to the amplitude of elastic scattering of WIMPs on quarks. Therefore WIMPs should interact, though weakly, with usual matter. Due to this interaction, WIMPs can elastically scatter on target nuclei and lead to a recoil of detector nuclei partially transferring energy to them. Therefore the search for the events of elastic scattering of WIMPs on detector nuclei is one of the prospective ways of galactic dark matter research.
Problem 5
Show that preservation of thermal equilibrium for a certain component in the expanding Universe is possible only under the condition $\Gamma\ll H$, where $\Gamma$ is the rate of reaction needed to support the equilibrium.
Preservation of the thermal equilibrium requires that the rate of the supporting reactions is much higher than the relative velocity of the temperature change: $$ \Gamma\gg \left|\frac{\dot T}{T} \right|. $$ Taking into account that $aT = const$ in the expanding Universe, one obtains $\dot T/T = - \dot a/a = - H.$ Thus the condition $\Gamma\gg \left|{\dot T}/{T} \right|$ is equivalent to the requirement \( \Gamma\gg H. \)
Problem 6
Show that at high temperatures $T\gg m_\chi$ ($m_\chi$ is the WIMPs mass) the ratio of equilibrium densities of WIMPs and photons is constant: $n_\chi^{eq}/n_\gamma^{eq}=const$.
In thermal equilibrium \[ n_\chi ^{eq} = \frac{g}{{\left( {2\pi } \right)^3 }}\int {f(\vec p)d\vec p}, \] where $g$ is the number of internal degrees of freedom, and $f(\vec p)$ is either Bose-Einstein or Fermi-Dirac distribution function. At high temperatures ($T \gg m_\chi $ ) $n_\chi ^{eq} \propto T^3$. For photons \[n_\gamma ^{eq} \simeq 0.244\left( {\frac{T}{\hbar c}} \right)^3. \] Therefore $n_\chi ^{eq} /n_\gamma ^{eq} = const$.
Problem 7
Show that the Boltzmann equation describing the evolution of WIMPs number density $n_\chi$ in particle number preserving interactions leads to the usual relation for non-relativistic matter $n_\chi\propto a^{-3}$.
The Boltzmann equation for WIMP number density reads \begin{equation}\label{11_10} \frac{dn_\chi }{dt} + 3Hn_\chi = - \left\langle {\sigma _A v} \right\rangle \left[ {n_\chi ^2 - \left( {n_\chi ^{eq} } \right)^2 } \right]. \end{equation} Here $n_\chi ^{eq} $ is the equilibrium WIMP number density. For the case $ n_\chi = n_\chi ^{eq}$ one immediately obtains the solution of the Boltzmann equation in the form $n_\chi\propto a^{ - 3} $.
Problem 8
Show that in the early Universe for $T\ge m_\chi$, the WIMPs number density follows its equilibrium value at temperature decreasing.
For early times $H\propto T^2 $, while $n_\chi\propto T^3 $, so the expansion rate decreases slower than the density. The term $3Hn_\chi$ can be neglected in the Boltzmann equation (\ref{11_10}) so that the density can follow its equilibrium value.
Problem 9
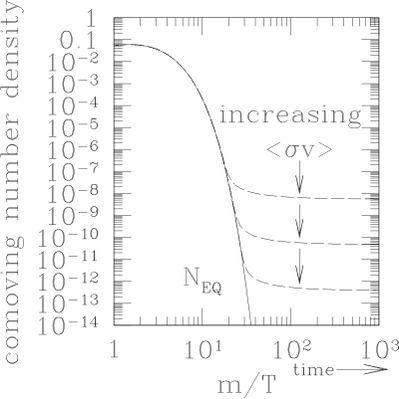
Show that decreasing of the annihilation cross-section leads to increasing of the relic density: contrary to Charles Darwin, the weakest wins.
High detection ability of a candidate particle in general does not assist, and even rather exclude, that the particle is the dominant component of the dark matter. It is due to the fact that the detection rate is proportional to the cross-section magnitude of the scattering (or annihilation) process, while the relic abundance is inversely proportional to it instead. Thus there is obvious anti-correlation between the detection rate and the cosmological abundance. It follows so that, in spite the natural desire of the experimenters, there is little hope to have a relic with both high abundance and high detection rate. The explanation is illustrated by the picture showing the evolution of particle number in early Universe.
Problem 10
What temperature does neutrino's density "freezing" take place at?
Problem 11
Considering the WIMPs as the thermal relics of the early Universe, estimate their current density.