Astronomy "before the Common Era"
Contents
- 1 Problem 1: Aristotle's geometry
- 2 Problem 2: Earth's radius
- 3 Problem 3: distance to the Moon
- 4 Problem 4: distance to the Sun
- 5 Problem 5: naked eye limitations
- 6 Problem 6: measuring distance to a satellite
- 7 Problem 7: orbits of planets
- 8 Problem 8: speed of light
- 9 Problem 9: Doppler shift
- 10 Problem 10: absorption lines
- 11 Problem 11: lines of calcium
- 12 Problem 12: getting rid of $c$
Problem 1: Aristotle's geometry
Aristotle knew there were stars, that one can see in Egypt but not in Greece. What conclusions could be made from this observation?
The Earth has the form of a ball with finite radius.
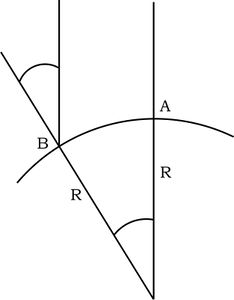
Problem 2: Earth's radius
How could Eratosthenes in 250 BCE determine the Earth's radius with the help of a well?
Problem 3: distance to the Moon
How could Aristarchus (310-230 BCE) compute the distance to the moon, knowing that it sets in about two minutes, and the maximum duration of a lunar eclipse is three hours?
Assuming that Sun is distant enough and lunar eclipses occur when the Earth shadows the Moon from the Sun, we conclude that Moon travels two Earth's radii in three hours. At the same time, Moon travels the distance of $2\pi d$ in one month. This information is enough to calculate that $d\approx 60 R_{\oplus}$.
Relative to the observer on Earth the Moon revolves around the Earth in one day $2\pi d=v\cdot 24\, h$. From the other hand, recalling that Moon gets beyond the horizon in approximately two minutes: $2r_{m}=v\cdot 2\,m$, we obtain the ratio between its diameter and the distance to the Earth: $r_{m}\approx d\cdot \pi/720\approx 0.25 R_{\oplus}$.
Problem 4: distance to the Sun
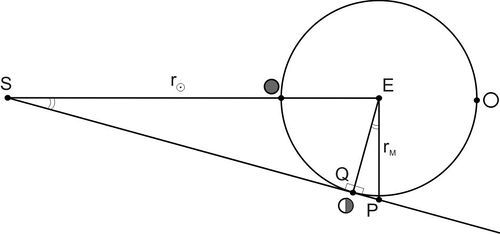
How can one calculate the size and distance to the Sun, while observing the phases and eclipses of the Moon?
It is well known that time between the quarter and new moon is in average $\tau=1~h$ greater than the time between quarter and full moon. Full moon occurs when Moon is at the opposite side of the Earth $E$ relative to the Sun $S$, while new moon occurs when it is on the same side. Quarter $Q$ is a phase when exactly half of the Moon's surface is illuminated and, thus, the angle Sun-Moon-Earth is $\pi/2$ (see figure). If $P$ is a point on the orbit where the angle Sun-Moon-Earth is right, then from similar triangles we obtain $ES/EQ=EQ/QP$ and, thus, \[\frac{r_{\odot}}{r_{M}}=\frac{r_{M}}{QP} =\frac{r_{M}}{2\pi r_{M}\cdot \tau/2T} =\frac{1}{\pi}\frac{T}{\tau},\] here $\tau=1~h$ and $T$ is the period of Moon revolution around the Earth, which equals to one month. Calculating, we set $r_{\odot}\sim1.50\cdot 10^{8}~km$, which is correct by the order of magnitude. The error is caused by not exact circularity of the Moon's orbit (the distance to the Moon is $405\cdot 10^3~km$ in apogee and $363\cdot10^3~km$ in perigee). Given the distances to the Sun and the Moon, recalling that their angular sizes are quite close, it's easy to estimate the size of the Sun.
Problem 5: naked eye limitations
Can one estimate how farther is the Sun than the Moon using only naked eye observations?
The Sun and the Moon can be usually seen together on the sky, so, analyzing the shape of the illuminated "crescent" of the Moon, we can estimate the angles in the triangle Earth--Moon--Sun. Thus, the angle Sun--Moon--Earth is $\pi/2$ for first quarter Moon or last quarter Moon. Measuring the angle between the directions to the Moon and to the Sun, we can calculate the acute angle with vertex at the Sun. This angle is just around 6 angular minutes! With the naked eye we can only ensure, that this acute angle is not greater than $1^\circ$ so that the Sun is at least 40 times farther than the Moon (while the exact number is 400).
Problem 6: measuring distance to a satellite
How to determine the distance to an Earth's satellite (Moon, for example) or to the Sun, using only a chronometer?
Since we observe their apparent daily motion from the surface of the planet and not from its center, the Sun, the Moon and sattelites of the Earth spend more time beyond the horizon than above it. It is easy to demonstrate, that for an observer at the sea level at equator the relative difference $\eta=\Delta T / T$ of the "day" and "night" durations relative to the luminary (?), which passes the zenith, is related to the Earth's radius $R_{\odot}$ as: $$ \sin {\pi \eta \over 2} = {R_0 \over R} $$ here $R$ is the radius of the star's orbit. For an artificial sattelite on the geostationary orbit, for example, the difference is $\Delta T \approx 70~m$ (in case when the sattelite orbits in antiphase with the Earth). For the Moon, correspondingly, $\Delta T \approx 15~m$, which is easily measurable with chronometer and, thus, the distance to the Moon could be calculated with high precision. But for the Sun we get $\Delta T \approx 2~s$, which is hard to measure even with a stopwatch.
Problem 7: orbits of planets
Ancient Babylonians knew, that apparent motion of Mars relative to the Earth is periodic with the orbital period 780 days (the synodic period of Mars). Tycho Brahe, in XVI century, measured the apperent Mars' trajectory with great precision. How could Johannes Kepler, using Brahe's data, accurately calculate the orbits of both Earth and Mars relative to the Sun and discover the laws named after him, which in time enabled Newton to biuld the classical theory of gravity?
Given the frequencies of the Earth's and Mars' revolution around the Sun, $\omega_1$ and $\omega_2$, we can calculate the apparent frequency of the Mars' revolution around the Earth, and it's period $T_{M}\approx 687\,\text{days}$. Then, using the data on Mars' location by Tycho Brahe with the period of 687 days (it will correspond to the same location of the Mars on its orbit) and triangulating, we can obtain the orbit of the Earth relative to the Sun and the Mars in corresponding position. Using the Earth's orbit and, again, different samples of Tycho Brahe's data with the period of 687 days, we can construct the orbit of the Mars by triangulation. Kepler's methods allowed to measure precisely the distances to the planets of Solar System.
Problem 8: speed of light
The orbital period of Io, one of the satellites of Jupiter, is equal to $42.5$ hours. In the 1670-ties Ole Rømer was measuring the time between two successive eclipses of Io when Earth moved on its orbit towards Jupiter and when it moved in the opposite direction. The noticed difference, about 20 minutes, allowed him to estimate the speed of light. Try to reproduce the reasonong and estimates of Rømer.
Rømer noticed that eclipses are delayed from strictly periodic "schedule" when the Earth is at the largest distance from Jupiter, and go ahead of "schedule", when the Earth is closest. The difference is caused by the finiteness of the speed of light, which has to travel the distance larger by $2\text{a.u.}\approx 3\cdot 10^8\,\text{km}$ (which was known at the moment only approximately, though). Thus, $c\approx 2a.u./1200\,\text{s}\approx 2.50\cdot 10^{5}\,\text{km/s}$. More accurate value can be obtained if we account for the actual delay around $16\,\text{min}\approx 10^3\,\text{s}$.
Problem 9: Doppler shift
In 1982 Doppler predicted the effect of change in the percieved frequency of oscillations when there is relative motion of emitter and detector. Doppler assumed that this effect can cause the difference in the color of stars: a star moving towards the Earth seems "bluer", while the one moving away "reddens". Explain why the Doppler effect cannot substantially change the color of a star.
The blue light from a moving away star shifts to the red part of the spectrum, but at the same time the portion of ultraviolet light of the star, which is invisible in normal conditions, shifts to the blue part of the visible spectrum, so that visible color of the star does not change. Stars have different colors mainly because of their different surface temperatures.
Problem 10: absorption lines
In the beginning of the XXth century J.F. Hartmann, a German astronomer, was studying the spectra of double stars. The wavelengths of their spectral lines shifted periodically due to their relative motion, with the period equal to the orbital one. In the spectra of some of the binaries he also noticed there were absorption lines with wavelengths that did not change with time. What discovery did Hartmann make due to this observation?
Hartmann understood that "unshifted lines" originate not in the outer layers of stars, but on their way from the star to the observer. This way the interstellar gas was first detected. This gas absorbs the starlight in narrow spectral intervals.
Problem 11: lines of calcium
Originally the interstellar gas was discovered by its absorption of spectral lines of calcium. Does that mean that calcium is the dominating component of the interstellar medium?
Interstellar gas reveals itself in other absoption lines too, for example in the well known yellow natrium line. Intensity of absorption is not necessarily determined by the abundance of corresponding element. It is rather determined by the "fortunate" location of energy levels, the transition between which realizes this line. Usually the lines which correspond to thansitions to the lowest excited state are most intensive. These lines are called resonant. The resonant lines of calcium and natrium lie in the visible part of the spectrum, while most of the resonant lines of other elements lie in the far ultraviolet part. Extraterrestrial radiation with wavelength smaller than 2900 A is completely absorbed by the Earth's atmosphere.
Problem 12: getting rid of $c$
One of the creators of the Theory of Relativity, Henry Poincare, when speaking in 1904 (!) of the fact that the speed of light $c$ enters all the equations of electromagnetism, compared the situation with the Ptolemy's geocentric theory of epicycles, in which the Earth's year enters all the relations for the relative motion of celestial bodies. Poincare expressed hope that a future Copernicus would rid electrodynamics of $c$. Recall other examples of blunders of geniuses.