Causal Structure
Contents
The causal structure is determined by propagation of light and is best understood in terms of conformal diagrams. In this section we construct and analyze those for a number of important model cosmological solutions (which are assumed to be already known), following mostly the exposition of [1].
In terms of comoving distance $\tilde{\chi}$ and conformal time $\tilde{\eta}$ (in this section they are denoted by tildes) the two-dimensional radial part of the FLRW metric takes form \begin{equation} ds_{2}^{2}=a^{2}(\tilde{\eta})\big[d\tilde{\eta}^2 -d\tilde{\chi}^2\big]. \label{ds2Dconf} \end{equation} In the brackets here stands the line element of two-dimensional Minkowski flat spacetime. Coordinate transformations that preserve the \emph{conformal} form of the metric \begin{equation*} ds_2^2 =\Omega^{2}(\eta,\chi)\big[d\eta^2 -d\chi^2 \big], \end{equation*} are called conformal transformations, and the corresponding coordinates $(\eta,\chi)$ -- conformal coordinates.
Problem 1
Show that it is always possible to construct $\eta(\tilde{\eta},\tilde{\chi})$, $\chi(\tilde{\eta},\tilde{\chi})$, such that the conformal form of metric (\ref{ds2Dconf}) is preserved, but $\eta$ and $\chi$ are bounded and take values in some finite intervals. Is the choice of $(\eta,\chi)$ unique?
Suppose $\tilde{\eta},\tilde{\chi}$ span infinite or semi-infinite values. Then we can always make the following sequence of coordinate transformations:
- Pass to null coordinates
\begin{equation} u=\tilde{\eta}-\tilde{\chi},\qquad v=\tilde{\eta}+\tilde{\chi}; \end{equation}
- Bring their range of values to a finite interval by some appropriate function, i.e.
\begin{equation} U=\arctan u,\qquad V=\arctan v. \end{equation}
- Go back to timelike and spacelike coordinates (this is not really necessary at this point and is done mostly for aesthetic reasons):
\begin{equation} T=V+U,\qquad R=V-U. \end{equation} Now the range of $(T,R)$ obviously covers some bounded region on the plane, while the radial part of the line element preserves its conformal form: \begin{equation} ds_2^2 \sim d\tilde{\eta}^2-d\tilde{\chi}^2 \sim du\, dv \sim dU\, dV \sim dT^2 -dR^2 . \end{equation} As the choice of function $\arctan$ was rather arbitrary (though convenient), the choice of conformal coordinates is not unique.
In this section we will reserve notation $\eta$ and $\chi$ and name "conformal coordinates/variables" to such variables that can only take values in a bounded region on $\mathbb{R}^2$; $\tilde{\eta}$ and $\tilde{\chi}$ can span infinite or semi-infinite intervals. Spacetime diagram in terms of conformal variables $(\eta,\chi)$ is called conformal diagram. Null geodesics $\eta=\pm \chi + const$ are diagonal straight lines on conformal diagrams.
Problem 2
Construct the conformal diagram for the closed Universe filled with
- radiation;
- dust;
- mixture of dust and radiation.
Show the particle and event horizons for the observer at the origin $\chi=0$ (it will be assumed hereafter that the horizons are always constructed with respect to this chosen observer).
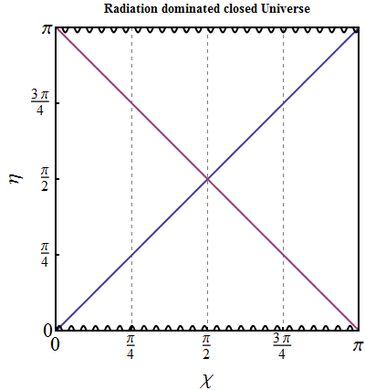
- Solution for $a(\eta)$ in a radiation dominated closed Universe is
\begin{equation} a=a_m \sin\eta ,\qquad \eta\in(0,\pi),\quad \chi \in [0,\pi]. \end{equation} As the ranges spanned by $\eta$ and $\chi$ are finite, they are already conformal coordinates. The conformal diagram is a square $\eta,\chi\in [0,\pi]$. Edges $\eta=0$ and $\eta=\pi$ correspond to the Big Bang and Big Crunch singularities respectively; worldline $\chi=\pi$ is the point on the three-sphere that is situated at the opposite pole with respect to observer at $\chi=0$.
The particle horizon is \[\eta=\chi,\] and event horizon is \[\eta=\eta_{max}-\chi =\pi -\chi.\] Both exist for all cosmological times: by the finite moment of the Big Crunch $\eta=\pi$ the event horizon is collapsed into a point (which is natural, as there is no more time left), while the particle horizon extends to the whole Universe. Thus only at the finite moment the whole of the Universe becomes observable. The farther the point, though, the younger will it look, of course, and the opposite pole will only be "observed" by our observer at the last moment of the Universe as it was at its creation.
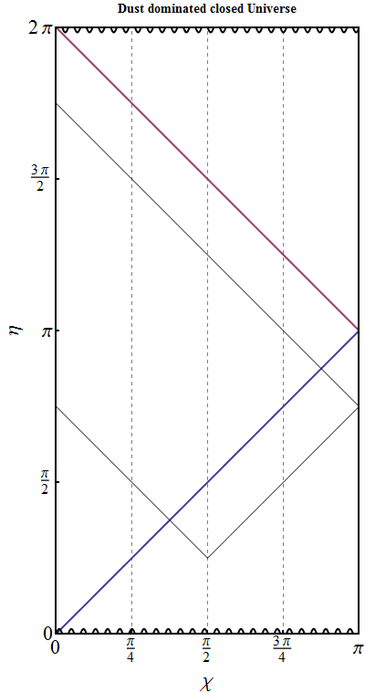
- Solution for $a(\eta)$ in a dust dominated closed Universe is
\begin{equation} a=a_m (1-\cos\eta) ,\qquad \eta\in(0,2\pi),\quad \chi \in [0,\pi]. \end{equation} The difference from the previous case is that $\eta$ spans twice the range, and $\eta_{max}=2\pi =2\chi_{max}$.
Therefore the event horizon is given by \[\eta=\eta_{max}-\chi=2\pi -\chi,\] so it exists only in the second, contracting, phase $\eta>\pi$. The particle horizon is given by $\eta=\chi$ again, but now it exists only during the expanding phase $\eta<\pi$. It encloses the full Universe at the moment of maximal expansion $\eta=\pi$ and for later times does not exist.
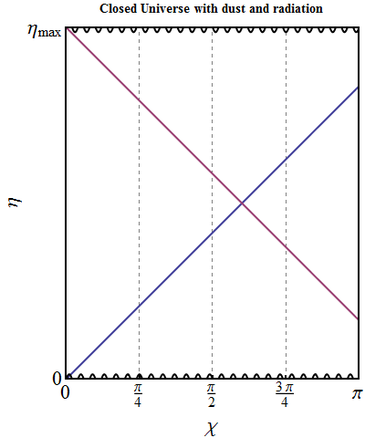
- Though the full analytic solution is more complicated, it is clear that the main features remain the same as in the previous considered cases. At early and late times, close to the singularities, the dynamics is determined by the radiation component. If there is enough dust, then at large enough scale factors (which may or may not be achieved depending on the initial conditions), which would correspond to the epoch around the maximal expansion, it will be dominating. The influence of dust is that dynamics is slowed down, so that depending on the ratio of densities
\[\eta_{max}\in [\pi,2\pi].\] Thus qualitatively the picture will be the same as in a dust dominated Universe: the conformal diagram is a rectangle, the event horizon exists only starting from some time $\eta_{e}=\eta_{max}-\pi$, while particle horizon, on the contrary, vanishes at $\eta_{p}=\pi$.
Problem 3
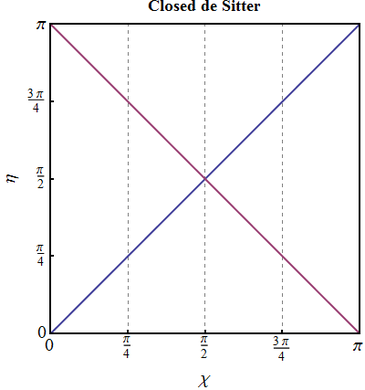
Closed dS. Construct the conformal diagram for the de Sitter space in the closed sections coordinates. Provide reasoning that this space is (null) geodesically complete, i.e. every (null) geodesic extends to infinite values of affine parameters at both ends.
The scale factor in the closed dS Universe is \begin{equation} a(t)=H_\Lambda^{-1}\cosh (H_\Lambda t),\qquad t\in (-\infty, +\infty), \end{equation} so on integration, for conformal time we obtain \begin{equation} \eta (t)=\int\limits_{-\infty}^{t}\frac{dt}{a(t)}=\arcsin\big[\tanh (H_\Lambda t)\big]+\frac{\pi}{2} \in (0,\pi). \end{equation} We choose the integration constant here so that $\eta=0$ corresponds to $t=-\infty$ and $\eta=\pi$ to $t=+\infty$. The full metric then can be written as \begin{equation} ds^{2}_{dS}=\frac{H_\Lambda^2}{\sin^2 \eta}\big[d\eta^2 -d\chi^2 -\sin^2 \chi d\Omega^2 \big]. \label{dSclosed} \end{equation} As the values of $\eta$ span a finite interval, $(\eta,\chi)$ are already conformal coordinates. The conformal diagram is again a square \begin{equation} \eta\in [0,\pi],\qquad \chi \in[0,\pi], \end{equation} with the difference from the radiation dominated Universe that the edges $\eta=0,\pi$ do not represent a singularity anymore, but instead correspond to infinite (and regular) past and future respectively. Both horizons are given again by \begin{equation} \eta_{e}=\pi-\chi,\qquad \eta_{p}=\chi \end{equation} and exist at all times. The spacelike boundaries of the conformal diagram correspond to $t\to \pm\infty$, and therefore to infinite values of affine parameter. This can be shown if one remembers the general formula for the cosmological redshift: \begin{equation} \text{const}=\omega a =\frac{dt}{d\lambda}a,\quad \Rightarrow\quad \lambda=\text{const}\cdot\int\limits^{t}dt \cosh(H_\Lambda t) \underset{t\to\pm\infty}{\longrightarrow}\infty . \end{equation} The timelike boundary of the diagram corresponds to the opposite pole, there is no real boundary there, the same as on a sphere: as particles propagate across the pole, their radial coordinate begins to decrease again, while the worldline on the conformal diagram is reflected from $\chi=\pi$. Thus by definition the spacetime is (null) geodesically complete.
Problem 4
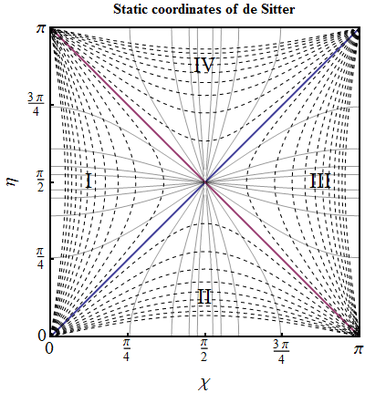
Static dS. Rewrite the metric of de Sitter space (\ref{dSclosed}) in terms of "static coordinates" $T,R$: \begin{equation} \tanh (H_\Lambda T)=-\frac{\cos\eta}{\cos\chi},\qquad H_\Lambda R =\frac{\sin\chi}{\sin\eta}. \end{equation}
- What part of the conformal diagram in terms of $(\eta,\chi)$ is covered by the static coordinate chart $(T,R)$?
- Express the horizon's equations in terms of $T$ and $R$
- Draw the surfaces of constant $T$ and $R$ on the conformal diagram.
- Write out the coordinate transformation between $(\eta,\chi)$ and $(T,R)$ in the regions where $|\cos\eta|>|\cos\chi|$. Explain the meaning of $T$ and $R$.
Let us introduce dimensionless coordinates $t=H_\Lambda T$ and $r=H_\Lambda R$. The inverse relations then are \begin{equation} \sin^2 \eta =\frac{1}{\cosh^2 t-r^2 \sinh^2 t}, \quad \sin^2 \chi =\frac{r^2}{\cosh^2 t-r^2 \sinh^2 t}. \end{equation} Using them, after some algebra from (\ref{dSclosed}) we get \begin{equation} ds_{dS}^2 =\big[1-H_\Lambda^2 R^2\big]dT^2 -\frac{dR^2}{1-H_\Lambda^2 R^2}-R^2 d\Omega^2 , \label{dSstatic} \end{equation} which resembles the Schwarzschild line element (and this is not a coincidence).
- As $|\tanh (H_\Lambda T)|<1$, we have $|\cos\eta| \leq |\cos\chi|$. This condition cuts out two out of four sectors from the square conformal diagram, I and III: one is $\eta\in [\chi, \pi-\chi]$ and the other is $\eta\in [\pi-\chi, \chi]$. In both $|\sin\eta|\geq |\sin\chi|$, so $R \leq H_{\Lambda}^{-1}$;
- The particle horizon $\eta=\chi$ corresponds to $R=H_\Lambda^{-1}$ and $T=-\infty$. It is one part of the boundary of the region (in two parts) covered by coordinates $(T,R)$. The event horizon $\eta=\pi-\chi$ corresponds to $R=H_\Lambda^{-1}$ and $T=+\infty$ and is the other part of the boundary of this region.
- $T=const$ is $\cos\eta =t\cos\chi $ and $R=const$ is $\sin\eta =r^{-1}\sin\chi$.
- In regions II and IV the needed relation is obtained if we simply replace $\tanh$ with $\coth$ in the first relation:
Problem 4
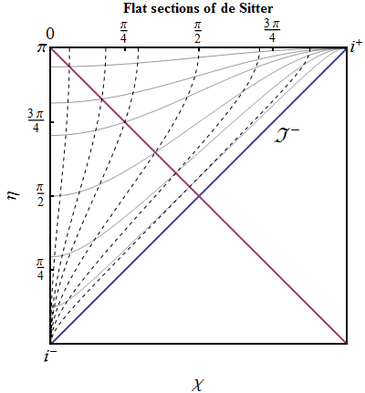
Flat dS. The scale factor in flat de Sitter is $a(t)=H_\Lambda^{-1} e^{H_\Lambda t}$.
- Find the range of values spanned by conformal time $\tilde{\eta}$ and comoving distance $\tilde{\chi}$ in the flat de Sitter space
- Verify that coordinate transformation
\begin{equation} \tilde{\eta}=\frac{-\sin\eta}{\cos\chi-\cos\eta},\qquad \tilde{\chi}=\frac{\sin\chi}{\cos\chi-\cos\eta} \end{equation} bring the metric to the form of that of de Sitter in closed slicing (it is assumed that $\tilde{\eta}=0$ is chosen to correspond to infinite future).
- Which part of the conformal diagram is covered by the coordinate chart $(\tilde{\eta},\tilde{\chi})$? Is the flat de Sitter space geodesically complete?
- Where are the particle and event horizons in these coordinates?
As $t\in(-\infty,+\infty)$, \begin{equation} \tilde{\eta} =\int\frac{dt}{a(t)}=H_\Lambda \int\limits_{+\infty}^{t}dt\; e^{-H_\Lambda t} =-e^{-H_\Lambda t} \in (-\infty,0). \end{equation} Here we choose $+\infty$ as the lower limit, because at $-\infty$ the integral diverges.
- Direct calculation yields (\ref{dSclosed}), with $\eta \in (0,\pi)$, $\chi\in (0,\pi)$;
- The upper triangle $\eta>\chi$, above the particle horizon, on which $\tilde{\eta}\to -\infty$. It is not geodesically complete, as geodesics are cut at the particle horizon.
- The particle horizon is the boundary of the patch of full dS space covered by flat slicing coordinates, and event horizon in these coordinates exists only in the latter part of evolution, for $\eta >\pi/2$.
Problem 5
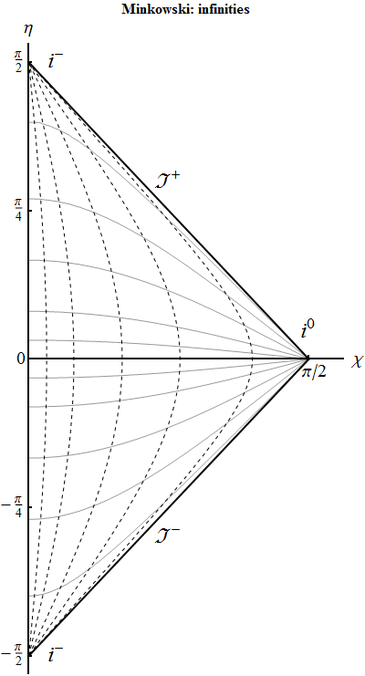
Infinities. What parts of the spacetime's boundary on the conformal diagram of flat de Sitter space corresponds to
- spacelike infinity $i^0$, where $\tilde{\chi}\to +\infty$;
- past timelike infinity $i^-$, where $\tilde{\eta}\to -\infty$ and from which all timelike worldlines emanate
- past lightlike infinity $J^-$, from which all null geodesics emanate?
- The one point at the left of the diagram;
- the one point at the bottom;
- the particle horizon.
Problem 6
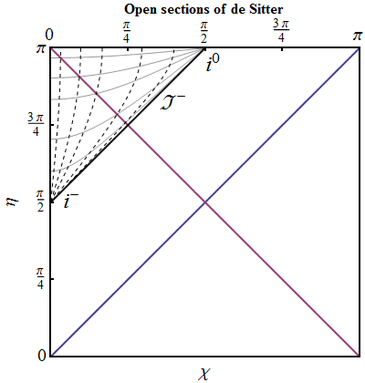
Open dS. Consider the de Sitter space in open slicing, in which $a(t)=H_\Lambda \sinh (H_\Lambda t)$, so conformal time is \begin{equation} \tilde{\eta} =\int\limits_{+\infty}^{t} \frac{dt}{a(t)}, \end{equation} where again the lower limit is chosen so that the integral is bounded.
- Find $\tilde{\eta}(t)$ and verify that coordinate transformation from $(\tilde{\eta},\tilde{\chi})$ to $\eta,\chi$, such that
\begin{equation} \tanh\tilde{\eta}=\frac{-\sin\eta}{\cos\cos\chi},\qquad \tanh\tilde{\chi}=\frac{\sin\chi}{\cos\eta} \end{equation} brings the metric to the form of de Sitter in closed slicing.
- What are the ranges spanned by $(\tilde{\eta},\tilde{\chi})$ and $(\eta,\chi)$? Which part of the conformal diagram do they cover?
After getting \begin{equation} \sinh \tilde{\eta}=-\frac{1}{\sinh(H_\Lambda t)}, \end{equation} the first part is checked straightforwardly; in the open de Sitter $\tilde{\chi}\in [0,+\infty)$, and $\tilde{\eta}\in(-\infty,0)$. The region covered by coordinates $(\tilde{\eta},\tilde{\chi})$ is $\{\eta>\chi+\pi/2\}$, only one eighth part of the full diagram.
Problem 7
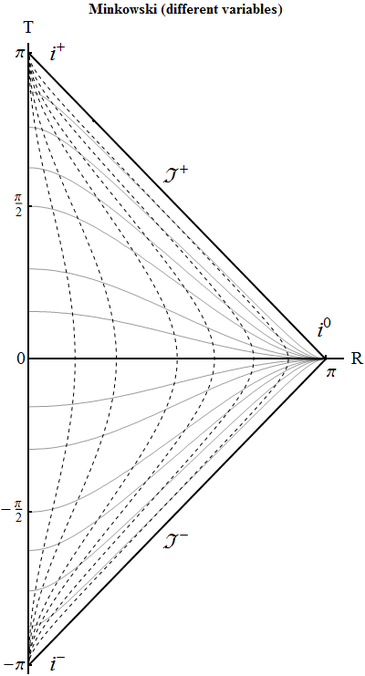
Minkowski 1. Rewrite the Minkowski metric in terms of coordinates $(\eta,\chi)$, which are related to $(t,r)$ by the relation \begin{equation} \tanh \tilde{\eta}=\frac{\sin\eta}{\cos\chi},\qquad \tanh \tilde{\chi}=\frac{\sin\chi}{\cos\eta} \end{equation} that mirrors the one between the open and closed coordinates of de Sitter. Construct the conformal diagram and determine different types of infinities. Are there new ones compared to the flat de Sitter space?
Coordinate transformation gives \begin{equation} ds^2 =\frac{1}{\cos^2 \chi -\sin^2 \eta}\big[d\eta^2 -d\chi^2 -\Psi^{2}(\eta,\chi)d\Omega^2 \big]. \end{equation} Here $r\in [0,+\infty)$ and $t\in (-\infty,+\infty)$. Comparing with the relation between $(\tilde{\eta},\tilde{\chi})$ with conformal coordinates $(\eta,\chi)$ in the open de Sitter universe, where $\tilde{\eta}\in (-\infty,0)$, we see that the difference is that $\tilde{\eta}$ spans $(-\infty,0)$, while now $t$ spans twice the range, $(-\infty,\infty)$. Therefore the conformal diagram is composed of two triangles, one the same as for open de Sitter and one for its time-reversed copy. Accordingly there now appear future timelike infinity $i^+$ and future lightlike infinity $J^+$.
Problem 8
Minkowski 2. The choice of conformal coordinates is not unique. Construct the conformal diagram for Minkowski using the universal scheme: first pass to null coordinates, then bring their span to finite intervals with $\arctan$ (one of the possible choices), then pass again to timelike and spacelike coordinates.
We start from spherical coordinates \begin{equation} ds^2 =dt^2 -dr^2 -r^2 d\Omega^2 . \end{equation}
- The first step is introducing null coordinates
\begin{equation} u=t-r,\quad v=t+r , \end{equation} so that \begin{equation} ds^2 =4du\,dv -\frac{(v-u)^2}{4}d\Omega^2 . \end{equation}
- Then bring the range of values to finite intervals
\begin{equation} U=\arctan u, \qquad V=\arctan v, \end{equation} so that \begin{equation} ds^2 =\frac{1}{4\cos^2 U \cos^2 V}\big[4dU\,dV -\sin^2 (V-U)d\Omega^2\big]. \end{equation} The whole spacetime is simply the half of the square $U,V\in (-\pi/2,\pi/2)$, in which $r>0$, i.e. $v>u\quad \Leftrightarrow\quad V>U$: on the plane $(U,V)$ it is the triangle \begin{equation} -\pi/2<U<V<\pi/2. \end{equation}
- Finally, go back to spacelike and timelike coordinates
\begin{equation} T=V+U,\qquad R=V-U \end{equation} so that metric becomes \begin{equation} ds^2 =\frac{1}{[\cos T +\cos R]^2}\big[dT^2 -dR^2 -\sin^2 R\; d\Omega^2\big]. \end{equation} The triangle is shrunken by $\sqrt{2}$ and rotated by $3\pi/4$ clockwise, thus turning into \begin{equation} \{R>0,\quad |T|<\pi/2 -R\}. \end{equation} This is the same form as obtained by the other construction (up to scaling, which is purely decorative).
Problem 9
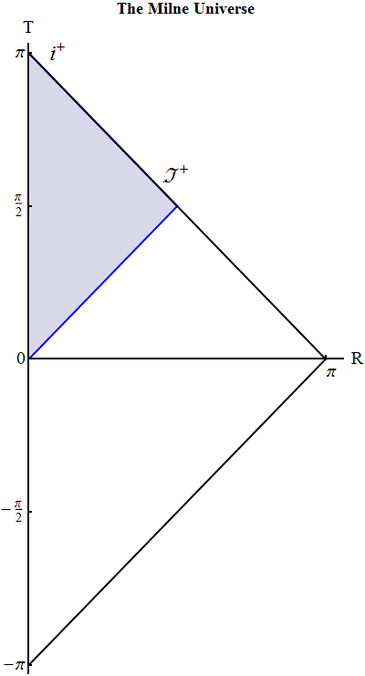
Draw the conformal diagram for the Milne Universe and show which part of Minkowski space's diagram it covers.
Minkowski metric $ds^2 =dT^2 -dR^2$, rewritten in terms of $(\tau, r)$ such that \begin{equation} T=\tau \cosh r ,\quad R=\tau \sinh r , \end{equation} is the metric of the Milne Universe. As Minkowski space is complete, the Milne Universe then is a \emph{part} of Minkowski in different variables. This part is where $T>R$. The boundary $T=R$ is the future light cone, so the whole Milne Universe is represented by the triangle homothetic to the whole space but 4 times smaller in area, with the common node of future infinity.
Problem 10
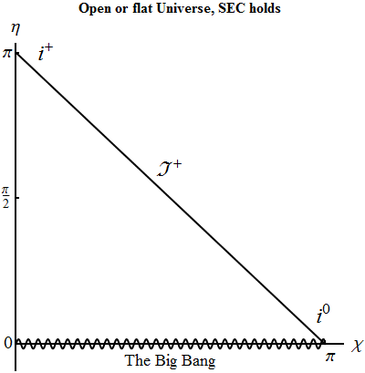
Consider open or flat Universe filled with matter that satisfies strong energy condition $\varepsilon +3p>0$. What are the coordinate ranges spanned by the comoving coordinate $\tilde{\chi}$ and conformal time $\tilde{\eta}$? Compare with the Minkowski metric and construct the diagram. Identify the types of infinities and the initial Big Bang singularity.
For flat Universe $\tilde{\chi}=r$, for the open $\tilde{\chi}=\sinh r$, so in both cases $\tilde{\chi}\in (0,+\infty)$. Strong energy condition implies that $w>-1/3$, so \begin{equation} \rho \sim a^{-3(1+w)}=a^{-n}, \end{equation} where $n>2$. From the first Friedman equation then after simple manipulations we obtain that \begin{equation} \frac{da}{dt}\sim a^{-\theta}, \end{equation} where $\theta$ is some positive number. Therefore both \begin{equation} t\sim \int da\; a^{\theta}, \quad\text{and}\quad \eta =\int \frac{da}{a}a^{\theta} \end{equation} converge at $a\to 0$ and diverge at $a\to \infty$. Consequently, the integration constant can be chosen so that $\eta\in (0,+\infty)$. The conformal structure is the same as that of the \emph{upper} half of Minkowski spacetime. The Big Bang singularity at $\eta=0$ is at the cut, and there are spacelike infinity, future infinity and future null infinity.
Problem 11
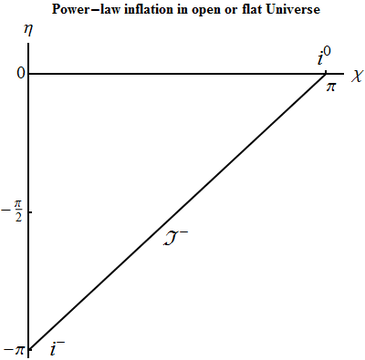
Draw the conformal diagram for open and flat Universes with power-law scale factor $a(t)\sim t^{n}$, with $n>1$. This is the model for the power-law inflation. Check whether the strong energy condition is satisfied.
As seen in the previous problem, if strong energy condition were satisfied, we would have $\dot{a}\sim a^{-\theta}$ with some positive $\theta$; this is not the case, so the condition is violated. As $t\in (0,+\infty)$, \begin{equation} \eta\sim \int \frac{dt}{t^n} \end{equation} diverges at small $a$ (thus also small $t$) and converges at $a\to \infty$ (thus as large $t$). So integration constant can be chosen so that $\eta\in (-\infty,0)$. The conformal structure is the same as \emph{lower half} of Minkowski spacetime. The cut is regular future infinity, and from Minkowski there are spacelike infinity, past null infinity, and past infinity. The point of past infinity corresponds to Big Bang and is singular.
- ↑ V.F. Mukhanov. Physical foundations of cosmology (CUP, 2005) ISBN~0521563984