Dark Matter Halo
Problem 1
Estimate the local density of the dark halo in the vicinity of the Earth, assuming that its density decreases as $\rho_g=C/r^2$.
\[M_g = 4\pi \int_0^{R_g } {\rho_g (r)} r^2 dr = 4\pi CR_g\Rightarrow\rho_g = \frac{M_g}{4\pi R_g r^2}.\] For $M_g\sim 10^{11} M_ \odot ,\;R_g \sim 10\mbox{kpc},\;r\sim 6.7\mbox{kpc}$ and assuming that the dark matter dominates in the halo, one obtains \[\rho _g \approx \rho _{_{DM}} \sim 10^{ - 25} \mbox{g/cm}^3\approx 0.2\mbox{ GeV/cm}^3.\]
Problem 2
Build the model of the spherically symmetric dark halo density corresponding to the observed galactic rotation curves.
The simplest halo model is the isothermic spherically symmetric one. The radial profile of the density in the model is restricted only by the observed rotation curves. This restriction leads to the following requirements for radial dependence of the density:
a) it must provide linear growth of the rotation curves at small distances.
b) it must follow as $1/r^2 $ for large distances, thus providing flat rotation curves.
The conditions are satisfied by the following function
\[
\rho (r) = \rho _0 \frac{r_c^2 + r_0^2}{r_c^2 + r^2}
\]
where $\rho _0 = \rho (r_0 )$ is the local halo density in vicinity of the Sun (if it concerns the dark halo in Milky Way) at $r = r_0 $ and $r_c$ is the core radius, inside which the density grows (with decreasing $r$ ) not faster than $1/r^2 $ and goes to constant, thus providing the linear growth of the rotation curves) at small $r.$
Problem 3
In frames of the halo model considered in the previous problem determine the local dark matter density $\rho_0$ basing on the given rotation velocities of satellite galaxies at the outer border of the halo $v_\infty\equiv v(r\rightarrow\infty)$ and in some point $r_0$.
Let some satellite galaxy orbits on the distance $r$ from the center of the main galaxy of mass $M\left( r \right)$ with velocity $v (r)$, then \[ \frac{v^2}{r} = G\frac{M(r)}{r^2}. \] As \[ M(r) = 4\pi \int_0^r {r'^2 \rho \left( {r'} \right)dr'}, \] then substitution of the expression for $\rho (r)$ (see problem) one obtains \[ v^2 (r) = 4\pi G\frac{1}{r}\int_0^r {r'^2 \rho \left( {r'}\right)dr'} = 4\pi G\rho _0 \left( {r_c^2 + r_0^2 } \right)\left[ {1 - \left( \frac{r_c}{r} \right)arctg\left( \frac{r}{r_0 } \right)} \right], \] so it follows that \[ v_\infty ^2 = v^2 \left( {r \to \infty } \right) = 4\pi G\rho _0\left( {r_c^2 + r_0^2 } \right) \] and \[ \rho _0 = \frac{v_\infty ^2}{4\pi G\left( {r_c^2 + r_0^2 }\right)}. \] From the other hand the core radius $r_c $ can be determined from the relation \[ \left( \frac{r_c}{r_0} \right)arctg\left( \frac{r_0}{r_c} \right) = 1 - \frac{v^2 \left( {r_0 }\right)}{v_\infty ^2}. \] Thus the local density and the core radius can be determined as soon as the rotation velocities $v\left( {r_0 } \right)$ and $v_\infty $ are measured.
Problem 4
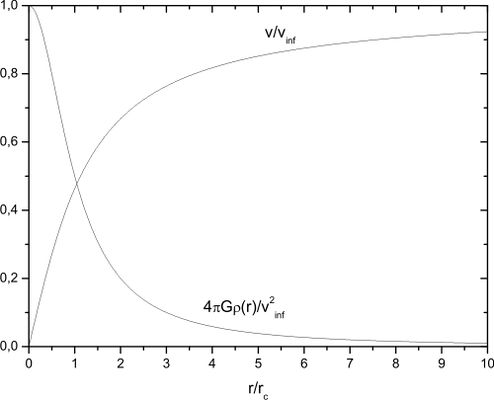
For the halo model considered in problem about halo model obtain the dependencies $\rho(r)$ and $v(r)$ in terms of $\rho_0$ and $v_\infty$. Plot the dependencies $\rho(r)$ and $v(r)$.
\[\rho \left( r \right) = \frac{v_\infty ^2}{4\pi G}\frac{1}{r_c^2 + r^2} ;\quad v(r) = v_\infty \sqrt{ 1 - \frac{r_c }{r} \arctan{\frac{r}{r_c}}} \] For $v_\infty = 220\mbox{km/s},\;r_c = 2.6\mbox{kpc},\,r_0 = 8\mbox{kpc}$ one obtains $\rho_0 \approx 5 \times 10^{ - 25} \mbox{g/cm}^3 \approx 0.3\,\mbox{GeV/cm}^3 $. The dependencies $\rho \left( r \right)$ and $v(r)$ are plotted on Figure.
Problem 5
Many clusters are sources of X-ray radiation. It is emitted by the hot intergalactic gas filling the cluster volume. Assuming that the hot gas ($kT\approx10keV$) is in equilibrium in the cluster with linear size $R=2.5Mpc$ and core radius $r_c=0.25Mpc$, estimate the mass of the cluster.
Equation of hydrostatic equilibrium reads: $$ \frac 1{\rho}\frac {dp}{dr}=-\frac {GM(r)}{r^2}, $$ where $p$ is pressure, and $\rho$ is density of the ideal gas with the state equation $p=nkT$, where $n$ is the concentration of the gas $n=\rho/m_p$. Let us assume the isothermic temperature distribution $T=const,$ then $$ \frac{kT}{m_p\rho}\frac{d\rho}{dr}=-\frac {GM(r)}{r^2}, $$ and it follows that $$ M(r)=-\frac{rkT}{Gm_p}\frac{d\ln\rho}{d\ln r}. $$ Using results of the problem $$ \rho(r) = \frac{v_\infty ^2}{4\pi G\left( {r_c^2 + r }\right)}, $$ one obtains $$ M(r)=2\frac{rkT}{Gm_p}\frac{r^2}{r_c^2 + r }\approx 10^{16}M_{\odot}. $$