Different Models of Inflation
There is a number of inflationary models. All of them deal with potentials of scalar fields which realize the slow-roll regime during sufficiently long period of evolution, then the inflation terminates and Universe enters the hot stage. It is worth noting that the models considered below are among the simplest ones and they do not exhaust all the possibilities, however they give the main idea about possible features of the evolution of scale factor in the slow-roll regime of inflation.
Contents
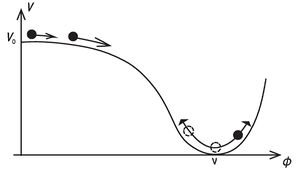
Chaotic Inflation (Inflation with Power Law Potential)
The chaotic inflation, or the inflation with high field, is considered as a rule with the power law potentials of the form $$V=g\varphi^n,$$ where $g$ is a dimensional constant of interaction: $$[g]=(\mbox{mass})^{4-n}$$ It should be noted that the slow-roll conditions for the given potential are always satisfied for sufficiently high values of the inflaton field $$\varphi\gg\frac{nM_{Pl}}{4\sqrt{3\pi}},$$ therefore the slow-roll takes place at field values which are great compared to Planck units.
Problem 1
Consider inflation with simple power law potential $$V=g\phi^n,$$ and show that there is wide range of scalar field values where classical Einstein equations are applicable and the slow-roll regime is realized too. Assume that the interaction constant $g$ is sufficiently small in Planck units.
Problem 2
Estimate the total duration of chaotic inflation in the case of power law potentials of second and forth order.
Problem 3
Express the slow-roll parameters for power law potentials in terms of $e$-folding number $N_e$ till the end of inflation.
Problem 4
Obtain the number $N$ of $e$-fold increase of the scale factor in the model $$V\left( \varphi \right) = \lambda \varphi ^4 \quad \left( {\lambda = 10^{ - 10} } \right).$$
Use the result of the previous problem to obtain for the power-law potential $V\left( \varphi \right) = \lambda \varphi ^n $ and $$ \varphi _i \gg \varphi _e $$ $$ N \sim \int_{\varphi _e }^{\varphi _i } \frac{\varphi d\varphi }{M_{Pl}^2 } \sim \frac{\varphi _i^2 }{M_{Pl}^2 }. $$ As $V(\varphi _i ) \sim M_{Pl}^4 $, in the considered model $\varphi _i \sim \lambda ^{ - 1/4} M_{Pl} $ and therefore $$ N \sim 10^5. $$
Problem 5
Estimate the range of scalar field values corresponding to the inflation epoch in the model $$V(\varphi ) = \lambda \varphi ^4 \left( {\lambda \ll 1} \right).$$
$$ V\left( {\varphi _0 } \right) \sim M_{Pl}^4 $$ For the considered potential $$ \phi _b \sim \lambda ^{ - 1/4} M_{Pl} \gg M_{Pl} $$ inflation will continue until the scalar field's amplitude decreases to a value of the order of Planck mass (see previous problem). Thus inflation period corresponds to the following interval of the scalar field's values $$ \lambda ^{ - 1/4} M_{Pl} < \phi < M_{Pl}. $$
Problem 6
Show that the classical analysis of the evolution of the Universe is applicable for the scalar field value $\varphi\gg M_{Pl}$, which allows the inflation to start.
For great values of scalar field $\varphi $ ($\varphi > M_{Pl} $), when the inflation process is possible, the energy density can still remain less than the Planck value, $M_{Pl}^4 $. Consider for example the potential $V\left( \varphi \right) = \lambda \varphi ^4 $, where $\lambda $ is a dimensionless coupling constant. Under the condition $\lambda \ll 1$ the energy density at $\varphi \sim M_{Pl} $ is less than the Planck one $V(\phi \sim M_{Pl} ) \sim \lambda M_{Pl}^4 \ll M_{Pl}^4.$
Problem 7
Find the time dependence for the scale factor in the inflation regime for potential $(1/n)\lambda\varphi^n$, assuming $\varphi\gg M_{Pl}$.
The condition $\left| \varphi \right| \gg M_{Pl} $ guarantees realization of the slow-roll regime, then $$ a(\varphi ) \simeq a_0 \exp \left( {8\pi G\int_\varphi ^{\varphi _0 } {\frac{V}[[:Template:V'(\varphi )]]d\varphi } } \right). $$ Therefore for any potential $V(\varphi ) = \left( {1/n} \right)\lambda \varphi ^n $ one obtains $$ a(\varphi (t)) \simeq a_0 \exp \left( {4\pi G/n\left( {\varphi _0^2 - \varphi ^2 (t)} \right)} \right). $$
Problem 8
The inflation conditions definitely break down near the minimum of the inflaton potential and the Universe leaves the inflation regime. The scalar field starts to oscillate near the minimum. Assuming that the oscillations' period is much smaller than the cosmological time scale, determine the effective state equation near the minimum of the inflaton potential.
Neglecting the expansion, represent the equation for scalar field $$ \ddot \varphi + 3H\dot \varphi + V'_\varphi = 0 $$ in the form $$ \frac{d}{dt}\left( {\varphi \dot \varphi } \right) - \dot \varphi ^2 + \varphi V'_\varphi = 0. $$ After averaging over the period of oscillations the first term turns to zero and therefore $$ \left\langle {\dot \varphi ^2 } \right\rangle \simeq \left\langle {\varphi V'_\varphi } \right\rangle . $$ The effective (averaged) equation of state reads $$ w \equiv \frac{p}{\rho } \simeq \frac{{\left\langle {\varphi V'_\varphi } \right\rangle - \left\langle {2V} \right\rangle }}{{\left\langle {\varphi V'_\varphi } \right\rangle + \left\langle {2V} \right\rangle }}. $$
Problem 9
Show that effective state equation for the scalar field, obtained in the previous problem for potential $V\propto\varphi^n$, in the case $n=2$ corresponds to non-relativistic matter and for $n=4$ - to the ultra-relativistic component (radiation).
Using the result of previous problem, for $V \propto \varphi ^n$ one obtains $$ w \simeq \frac{n - 2}{n + 2}. $$ The case $n = 2$ corresponds to $w = 0$ (non-relativistic matter), and $w = 1/3$ - to $n = 4$ (radiation).
Problem 10
Obtain the time dependence of scalar field near the minimum of the potential.
Let the potential have a minimum at $\varphi = 0$ and in the vicinity of the minimum $$ V(\varphi ) = \frac{m^2 \varphi ^2 }{2}. $$ The equation of motion for the scalar field in this potential reads $$ \ddot \varphi + 3H\dot \varphi + m^2 \varphi = 0. $$ Substitution $\varphi (t) = a^{ - 3/2} \chi (t)$ makes transition to an oscillator with variable frequancy and enables us to get rid of the first derivative $$ \ddot \chi + \left( {m^2 - \frac{3}{2}\frac{\ddot a}{a} - \frac{3}{4}\frac{\dot a^2 }{a^2 }} \right)\chi = 0. $$ In the regime of fast oscillations ($m^2 \gg H^2$) $$ \chi (t) = A\cos \left( {mt + \alpha } \right) $$ and the scalar field approaches the minimum as $$ \varphi(t) = Ca^{ - 3/2}\cos (mt + \alpha ). $$
Problem 11
Find the energy-momentum tensor of a homogeneous scalar field in the regime of fast oscillations near the potential's minimum.
Use the solutions $\varphi (t)$ obtained in the previous problem for potential \[V(\varphi ) = \frac{m^2 \varphi ^2 }{2}\] and the definitions $$ T_{00} = \frac{1}{2}\dot \varphi ^2 + V\left( \varphi \right) = \rho _\varphi ;\quad T_{ij} = \left( {\frac{1}{2}\dot \varphi ^2 - V\left( \varphi \right)} \right)\delta _{ij} = p_\varphi \delta _{ij} $$ to obtain $$ T_{00} = \rho _\varphi = a^{ - 3} \frac{m^2 C^2 }{2};\quad T_{ij} = p_\varphi \delta _{ij} = - a^{ - 3} \frac{m^2 C^2 }{2}\cos \left( {2mt + 2\alpha } \right). $$ Average over the oscillation period to find the energy-momentum tensor for non-relativistic matter: $\rho \propto a^{ - 3} ,~p = 0$.
Problem 12
Check whether the chaotic inflation model agrees with the experimental data, which give the value $r=\mathcal{P}_\mathcal{T}/\mathcal{P}_\mathcal{R}<0.2$ for the tensor perturbation amplitude and $n_s=0.94\div 0.99$ for the spectrum slope. For the inflaton potential take $V(\varphi)=m^2\varphi^2/2$.
Problem 13
Consider chaotic inflation with potential $V(\varphi)=m^2\varphi^2/2$ and obtain the difference between the spectrum slopes for the waves corresponding to cosmological perturbations of sizes $100\ kpc$ and $10\ Gpc$.
Problem 14
What is the difference between the chaotic inflation model by Linde and its original version by Starobinsky--Guth?
In the chaotic inflation model the inflationary expansion stage appears at any conditions compatible with the inflationary expansion, and not necessarily in the minimum of the scalar field potential, as in the original version.
The Novel Inflation (the Inflation Near Minimum of the Potntial)
As the reader might notice in the previous subsection, the chaotic inflation requires to include the super-Planck field values, however it is worth noting that there is an inflation model free of such requirement. Conditions of possible inflation start in this model considerably differ from the chaotic initial data. At the same time the flatness requirement for the inflaton potential is present in this model too.
Consider an inflaton potential shown on figure and assume that for small $\varphi$ it takes the form $$V(\phi)=V_0-g\phi^n,$$ where $n\geq 3$. The most often considered potential is the forth order one $$V(\phi)=V_0-\frac{\lambda}{4}\phi^4.$$ The inflation model with such potential is called novel inflation.
Problem 15
Show that the inflation regime can start without super-Planck values of the inflaton field. Consider potential of the form \[V(\varphi)=V_0-\frac{\lambda}{4}\varphi^4.\]
Problem 16
Consider the inflation model in which the inflaton potential for small $\varphi$ takes the form $$V(\varphi)=V_0-\frac\lambda 4\varphi^4.$$ Assume that the slow-roll regime terminates at comparably small value of the inflaton field, so that $\lambda \varphi^4_e\ll V_0$, to obtain the ratio $\epsilon/|\eta |$. Determine which of the two parameters reaches unity first.
Problem 17
Using the results of the previous problem and the condition $\lambda \varphi^4_e\ll V_0$, obtain the inequality giving the condition for realization of the novel inflation scenario.
Problem 18
For the model of problem 16 obtain the post-inflation heat up temperature $T_{reh}$.
Problem 19
For the model of problem 16 determine the relation between the inflaton field value on the inflation stage and the $e$-folding number till the end of inflation.
Problem 20
For the model of problem 16 determine the relation between the slow-roll parameters and the $e$-folding number till the end of inflation.
Problem 21
Estimate the duration of novel inflation.
Problem 22
Obtain the relation $$\eta=-\frac{n-1}{n-2}\frac{1}{N_e}$$ for the novel inflation model with the potential of the form $V(\varphi)=V_0-g\varphi^n,$ where $n\geq 3$.
Inflation with Exponential Potential (the Power Law Inflation)
Problem 23
Find the scalar field potential that gives rise to the power law for the scale factor growth \[a(t)\propto {{t}^{p}}.\]
Using the Friedman equation express $V(\varphi )$ and $\dot{\varphi }$ in terms of $H$ and $\dot{H}$. This allows one to write down the system of equations describing the parametric dependence of $V$ on $\varphi$ \[\begin{aligned} & V=\frac{3{{H}^{2}}}{8\pi G}\left( 1+\frac{{\dot{H}}}{3{{H}^{2}}} \right), \\ & \varphi ={{\int{dt\left( -\frac{{\dot{H}}}{4\pi G} \right)}}^{1/2}} . \end{aligned}\] Exclude the time variable using the relation \[\frac{\varphi }{{{M}_{Pl}}}=\sqrt{\frac{p}{4\pi }}\ln t,\] and for the power law \[a(t)\propto {{t}^{p}}\] find \[V\left( \varphi \right)={{V}_{0}}\exp \left( -\sqrt{\frac{16\pi }{p}}\frac{\varphi }{{{M}_{Pl}}} \right).\] The obtained result implies that the scalar field in the obtained potential under condition $p>1$ can be treated as dark energy, i.e. it provides the accelerated expansion of the Universe.
Problem 24
Find the exact particular solution of the system of equations for the scalar field in potential $V(\varphi)=g\exp(-\lambda\varphi)$.
Problem 25
Compare the solution obtained in the previous problem with the solution of evolution equations for the scalar field in the expanding Universe in the inflation limit.
Problem 26
Show that dependence \[H(\varphi)\propto\exp\left(-\sqrt{\frac{1}{2p}}\frac{\varphi}{M_{Pl}}\right)\] leads to power law inflation $a(t)=a_0 t^p$.
Problem 27
Show that dependence $H(\varphi)=\varphi^{-\beta}$ leads to the so-called intermediate inflation (the Universe expansion goes faster than any power law and slower than the exponential one), such that \[a(t)\propto\exp(At^f),\ 0<f<1,\quad A>0,\quad f=(1+\beta/2)^{-1}.\]
Problem 28
Consider the inflation model with potential $V(\varphi)=\Lambda\exp (-\varphi/\varphi_0)$ and obtain the field values at which the slow-roll conditions are satisfied. Assume that inflation terminates at $\varphi=\varphi_1$.
Problem 29
Consider the inflation model of the previous problem and obtain the initial value of the field required to prolong the inflation for $N_e\gtrsim 60$ $e$-foldings. What value of $\Lambda$ gives the correct amplitude $\delta\rho/\rho\simeq\sqrt{\mathcal{P}_\mathcal{R}}\simeq 5\cdot 10^{-5}$ of the scalar perturbations?
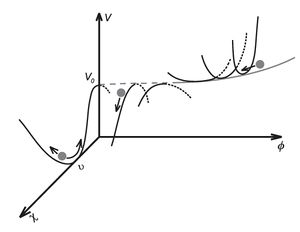
The Hybrid Inflation
One more inflation model free of super-Planck fields is called the \textbf{hybrid inflation}. In the simplest version this model contains two scalar fields---the inflaton field $\varphi$ and an additional field $\chi$ (see figure). During the inflation stage the field $\varphi$ is high, and the system slowly rolls along the valley $\chi =0$. After that the valley $\chi =0$ transforms into a saddle, the fast roll takes place in perpendicular direction, the inflation terminates, and the oscillations near the minimum $\varphi =0,$ $\chi=\nu$ lead to the heat up of the Universe.
The potential of inflaton field for the hybrid inflation takes the form \begin{equation}\label{gibrid_inf_v} V(\varphi,\chi)=\frac12\left(g^2\varphi^2-\mu^2\right)\chi^2+\frac h4\chi^4+U(\varphi)+V_0, \end{equation} where $g$ and $h$ are positive dimensionless constants, $\mu$ is a parameter of dimension of mass, $U(\varphi)$ is the monotonically growing inflaton potential.
Problem 30
Consider the hybrid inflation model with potential of the form \ref{gibrid_inf_v}, where $U(\varphi=0)=0$ and $U(\varphi)=m^2\varphi^2/2$. The potential $V(\varphi,\chi)$ has maximum at $\varphi=0$, $\chi=\nu=\mu/\sqrt{h}.$ The constant $V_0$ is determined from the requirement that the value at the minimum is zero, resulting in $$V_0=\frac{\mu^4}{4h}.$$ The line $\chi=0$ represents the valley of the potential $V(\varphi, \chi)$ at $\varphi > \varphi_c,$ where $\varphi_c=\mu/g.$ Consider the case when the contribution of the inflaton field to the total energy at the critical value of the former is small \begin{equation}\label{gibrid_inf_full_energy} U_c\equiv U(\varphi_c)\ll V_0. \end{equation} Obtain the slow-roll parameters under the requirement that inflation endures up to the moment when it rolls down the critical value $\varphi_c$ ($\varphi\gg\varphi_c$), and show that inflation can take place at sub-Planck values of the inflaton field.
Problem 31
Consider the inflation model of problem \ref{inf_gibrid_1} and obtain the value of $V_{eff}(\chi)$ corresponding to field value $\chi$, at which it starts to roll down to the minimum $\varphi=0$ after the Hubble time $\Delta t \sim H^{-1}(\varphi_c)$ and $\chi = \nu$ after the inflaton reaches the critical value $\varphi_c$.
Problem 32
Obtain the value $\eta_\chi$ corresponding to the fast roll down of the field $\chi$ along the potential $V_{eff}(\chi)$ (see the previous problem).
Problem 33
Use the results of problems 30-32, the condition $U_c\equiv U(\varphi_c)\ll V_0$ and assume that the critical value of the inflaton field is small compared to the Planck mass to obtain the chain of inequalities giving the conditions to realize the hybrid inflation scenario.
Problem 34
Obtain the dependence of the $e$-folding number till the inflation's end on the inflaton field value.
Problem 35
Obtain relation between $\eta$ and $N_e$ for the hybrid inflation model in the case of quadratic potential.
Problem 36
Consider the hybrid inflation model with $U_c\sim V_0$. Show that in this case $\varphi_c\gtrsim M_{Pl}.$ What region of the $(\epsilon,\eta)$ plane corresponds to the models of such type?
Other Types of Inflation
Problem 37
Formulate the differences between the models of cold and warm inflation.
The difference between warm and cold inflation is in the fact that the former is free of separate warming stage. The radiation generation process competes with the inflationary expansion. Realization of inflation requires that the vacuum energy density dominates (in order to create the accelerated expansion). However this condition does not exclude The existence of considerable density of radiation energy during the inflation process. Presence of the radiation during inflation allows to smoothen the end of inflation and transit to the radiation-dominated epoch without a special warming phase. Such scenario can be realized if vacuum energy density falls down faster than that of radiation, so that at some point a smooth intersection occurs. This enables one to solve the problem of exit from the inflation.
Problem 38
The Standard Model of elementary particles allows instability of baryons, which can decay to leptons. But as the rate of the processes violating the baryon number conservation is very low (for example, the proton lifetime $\tau_p\ge10^{30}years$), it is extremely difficult to find experimental proofs of the proton instability. Try to formulate the "inflationary proof" of the proton instability.
It is only the spatially flat Universe where parallel lines do not intersect. Such geometry is naturally provided by the inflationary cosmology. This theory assumes that density of all elementary particles was negligibly small at the end of the inflationary expansion. All matter came into being as the result of the decay of the scalar field at the end of inflation. The proton density in the observed Universe is much higher than that of antiprotons. This means that total density of baryons at present is non-zero. We could not transit to such situation from the post-inflation stage if the baryon number was conserved. Then a non-trivial conclusion follows that the observed Euclidean geometry and homogeneity of the Universe require violation of conservation of the baryon number. In other words, the fact that the parallel lines do not intersect in our Universe proves the instability of proton.
Problem 39
In what way is the inflation theory related to the solution of the problem: why is mathematics so efficient in description of our world and prediction of its evolution?
Consider the following example [A.Linde, arXiv:hep-th/0211048 (2002)]. Assume that inflation is absent. Then the Universe and the reader himself are in stable or meta-stable vacuum state with Planck density $\rho _{Pl} \sim M_{Pl}^4 $. Such Universe is governed by quantum gravity and quantum fluctuations of the space-time are of order of the curvature. It seem that due to the quantum fluctuations our measuring devices (rulers and clocks) are destroyed sooner than we can perform a measurement. Mathematics looses any efficiency, because it is impossible to compare mathematical predictions with the experiment or measurement.