Interactions in the Dark Sector
Dark energy is the main component of the Universe's energy budget, thus it is necessary to consider the possibility of its interaction with other components of the Universe, in particular with the component second in importance - the dark matter. Additional interest to that possibility is related with the fact that within its framework it is possible to solve the so-called "coincidence problem": the coincidence by the order of magnitude (at present) of dark energy and dark matter densities (0.7 and 0.3 respectively). As the nature of those two components is yet unknown, we cannot describe interaction between them starting from the first principles and we are forced to turn to phenomenology. In the base of the phenomenology one can put the conservation equation \[\dot\rho_i+3H(\rho_i+p_i)=0.\] In the case of interaction between the components it is necessary to introduce the interaction (a source) into the right-hand side of the equation. It is natural to assume that interaction is proportional to the energy density multiplied by a constant of inverse time dimension. For that constant it is natural to choose the Hubble constant.
Contents
General Analysis
Problem 1
Construct a model of the Universe containing only interacting dark energy and dark matter, while their total energy density is conserved.
A general coupling between a dark energy (with density $\rho _{_{DE}}$) and dark matter (with density $\rho _{_{DM}}$) may be described in the background by the modified conservation equation
\[
\begin{array}{l}
\dot \rho _{_{DM}} + 3H\rho _{_{DM}} = Q, \\
\dot \rho _{_{DE}} + 3H\left( {\rho _{_{DE}} + p_{_{DE}} } \right) = - Q.
\end{array}
\]
Here $Q$ is the rate of energy density exchange in the dark sector. Sign of $Q$ determines the direction of energy transfer: if $Q < 0$, then dark matter continuously decays into the dark energy, if $Q > 0$ - the opposite process takes place.
A satisfactory model requires that $Q$ should be expressed in terms of the energy densities and other covariant quantities.
Problem 2
Within the framework of problem, find the effective state parameters $w^{(\varphi)}_{eff}$ and $w^{(m)}_{eff}$ that would allow one to treat the components as non-interacting.
We can define effective equation of state parameters as \[ \begin{array}{l} \dot \rho _{_{DM}} + 3H(1+w_{DM,eff})\rho _{_{DM}} = 0 \\ \dot \rho _{_{DE}} + 3H(1+w_{DE,eff})\rho _{_{DE}} = 0 \end{array} \] This definition implies that \[ w_{DM,eff}=-\frac{Q}{3H\rho _{_{DM}}},\ w_{DE,eff}=w_{DE}+\frac{Q}{3H\rho _{_{DE}}} \]
Problem 3
Using the effective state parameters obtained in the previous problem, analyze dynamics of dark matter and dark energy depending on sign of the rate of energy density exchange in the dark sector.
\[ {\it if}\ Q<0 \Rightarrow\left\{ \begin{array}{ll} w_{DM,eff}>0 & {\it dark\ matter\ redshifts\ faster\ than}\ a^{-3}\\ w_{DE,eff}<w_{DE} & {\it dark\ energy\ has\ more\ accelerating\ power} \end{array} \right. \] \[ {\it if}\ Q>0 \Rightarrow\left\{ \begin{array}{ll} w_{DM,eff}<0 & {\it dark\ matter\ redshifts\ slower\ than}\ a^{-3}\\ w_{DE,eff}>w_{DE} & {\it dark\ energy\ has\ less\ accelerating\ power} \end{array} \right. \]
Problem 4
Show that the coupling quintessence behaves like a phantom uncoupled model, but without any negative kinetic energy.
Use the result of the previous problem. When $Q<0$ it is possible that $w_{DE,eff}<-1$. This means that the coupling quintessence behaves like a phantom uncoupled model, but without any negative kinetic energy. (Dynamics of dark energy with a coupling to dark matter, Christian G. Bohmer, Gabriela Caldera-Cabral, Ruth Lazkoz, and Roy Maartens, 0801.1565)
Problem 5
Show that within the framework of the model of the Universe described in problem the Klein-Gordon equation for the scalar field takes the form: $$ \ddot{\varphi}+3H\dot{\varphi}+\frac{dV}{d\varphi}=-\Gamma ,\; \Gamma \equiv \frac{Q}{\dot{\varphi}} $$ Here $Q$ is the constant of interaction between dark energy and dark matter.
Substitution of the energy density and pressure of the scalar field into the conservation equation with the source $Q$ gives the following: \[\dot{\varphi}\ddot{\varphi}+3H\dot{\varphi}^2+\frac{dV}{d\varphi}\dot{\varphi}=Q\] and the required result follows immediately.
Problem 6
The dynamics of present Universe is assumed to be dominated by dark energy and dark matter. In frame of the model of interacting dark energy and dark matter (see problem) obtain equations for the densities $\rho_{DE}$ and $\rho_{DM}$ under assumption that $Q=-3H\Pi$, where the quantity $\Pi$ can be considered as the effective pressure.
It is convenient to introduce the ratio $r\rho_{DM}/\rho_{DE}$ of the energy densities, which is characterized by the dynamics \[\dot r=r\left[\frac{\dot\rho_{DM}}{\rho_{DM}}-\frac{\dot\rho_{DE}}{\rho_{DE}}\right]\] and to replace the derivatives with respect to the cosmic time by derivatives with respect to $\ln a^3$ , denoted by a prime, $\dot\rho_i=3\rho'_iH$. Then the dynamics of the two-component system is given by \[\frac{\rho'_{DM}}{\rho_{DM}}=-1-\frac{\Pi}{\rho_{DM}}\] \[\frac{\rho'_{DE}}{\rho_{DE}}=-(1+w)+\frac{\Pi}{\rho_{DE}},\ w=\frac{p_{DE}}{\rho_{DE}}\] Or, alternatively, by \[\rho'=-\left(1+\frac{w}{1+r}\right)\] \[r'=\left[w-\frac{(1+r)^2}{r\rho}\Pi\right]r,\ \rho=\rho_{DE} +\rho_{DM}\] (F.Arevalo, A.Bacalhau and W. Zimdahl, arXiv: 1112.5095)
Problem 7
For the scalar field $\varphi$ in the form of quintessence use the variables \[x^2=\frac{\kappa^2\dot\varphi^2}{6H^2},\ y^2=\frac{\kappa^2V}{3H^2}\] to express the total equation of state parameter $w_{tot}\equiv p_{tot}/\rho_{tot}$, quintessence state parameter $w_\varphi\equiv p_\varphi/\rho_\varphi$, deceleration parameter $q$ and determine the allowed variation range of the parameters. The Universe is assumed to be flat.
\[\rho_\varphi=\frac{3H^2}{\kappa^2}(x^2+y^2),\ p_\varphi=\frac{3H^2}{\kappa^2}(x^2-y^2)\] \[w_\varphi=\frac{p_\varphi}{\rho_\varphi}=\frac{x^2-y^2}{x^2+y^2},\ w_{tot}=\frac{p_\varphi}{\rho_{tot}}=\frac{x^2-y^2}{\Omega_{tot}}=x^2-y^2\] \[q=-\frac{\ddot a}{aH^2}=\frac12+\frac32(x^2-y^2)\] Relation $\Omega_{tot}=1$ implies that $x^2+y^2\le1$.
Linear Models
Problem 8
Show that the energy balance equation (modified conservation equations) for $Q\propto H$ or $Q\propto\dot\varphi$ are independent from $H$ when expressed in the variables $x(N), y(N)$ where $N=\log a$ thus phase space of such coupling model is two-dimensional $(x,y)$ space.
The required statement can be easily proved by the replacement $\dot\rho\rightarrow\rho'H$ ($\dot\varphi\rightarrow\varphi'H$) in the energy balance, where prime denotes $d/dN$.
Problem 9
Use the variables $(x,y)$, introduced in the problem in order to obtain the system of equations describing the quintessence in the potential \[V(\varphi)=V_0\exp(-k\lambda\varphi),\] where $k^2\equiv8\pi G$, $\lambda$ is a dimensionless constant and $V_0>0$, in the case of flat Universe and under assumption $Q=\alpha H\rho_{DM}$
The autonomous system of equation in this case is \[x'=-3x+\lambda\frac{\sqrt6}{2}y^2+\frac32x(1+x^2-y^2)+\alpha\frac{1-x^2-y^2}{2x},\] \[y'=\lambda\frac{\sqrt6}{2}xy+\frac32y(1+x^2-y^2),\] where a prime denotes $d/dN$.
Problem 10
Find the scale factor dependence for the dark matter density assuming that the constant of interaction between the dark matter and the dark energy equals $Q=\delta(a)H\rho_{DM}$.
\[ \rho _{_{DM}} = \rho _{_{DM0}} a^{ - 3} \exp \left( {\int {\delta d\alpha } } \right);\quad \alpha \equiv \ln a. \]
Problem 11
Find the scale factor dependence for the dark matter and energy densities assuming that $Q=\delta H\rho_{DE}$ $(\delta=const)$.
\[ \begin{gathered} \rho _{_{DE}} = \rho _{_{DE0}} a^{ - \left[ {3(1 + w_{_{DE}} ) + \delta } \right]} ; \\ \rho _{_{DM}} = \frac{{ - \delta \rho _{_{DE0}} }} {{3w_{_{DE}} + \delta }}a^{ - \left[ {3(1 + w_{_{DE}} ) + \delta } \right]} + \left( {\rho _{_{DM0}} + \frac{{\delta \rho _{_{DE0}} }} {{3w_{_{DE}} + \delta }}} \right)a^{ - 3}. \end{gathered} \]
Problem 12
Let the dark energy state equation be $p_{DE}=w\rho_{DE}$, where $w=const$. Within the framework of problem, find the dependence of the dark energy density on scale factor, assuming that $\rho_{DM}=\rho_{DM0}a^{-3+\delta}$, where $\delta$ characterizes the deviation of the dark matter density's evolution from the standard one (in the absence of interaction).
In the considered model $$ \dot{\rho }_{_{DM}} +3\frac{\dot{a}}{a} \rho _{_{DM}} =-\dot{\rho }_{_{DE}} -3\frac{\dot{a}}{a} \left(\rho _{_{DE}} +p_{_{DE}} \right). $$ Inserting $\rho_{_{DM}} =\rho _{_{DM,0}} a^{-3+\delta } $ into the latter equation and integrating the obtained differential equation, one obtains $$ \rho _{_{DE}} (a)=\rho _{_{DE0}} a^{-3(1+w)} +\frac{\delta \rho _{_{DM0}} }{3\left|w\right|-\delta } a^{-3+\delta } $$ It is evident that in absence of interaction between the components the latter equation reproduces the usual scale factor dependence for quintessence (or cosmological constant for the case $w=-1$).
Problem 13
Let the densities' ratio in model of interacting dark energy and dark matter has the form \[\frac{\rho_{DM}}{\rho_{DE}}\propto Aa^{-\xi}.\] Determine the interaction $Q$ between the components.
\begin{equation} \frac{\rho _{_{DM}}} {\rho _{_{DE}}} \propto Aa^{ - \xi } \label{44_1} \end{equation} \begin{equation} \begin{gathered} \dot \rho _{_{DM}} + 3H\rho _{_{DM}} = Q; \\ \dot \rho _{_{DE}} + 3H\rho _{_{DE}} (1 + w_{_{DE}} ) = - Q;\label{44_2} \\ \end{gathered} \end{equation} Let us show that appropriate choice of the interaction $Q$ allows to reproduce the required behavior of the density ratio$\frac{\rho _{_{DM}}}{\rho _{_{DE}}}.$ From the equation (\ref{44_1}) \begin{equation} \rho _{_{DE}} = \frac{\rho _{_{DM}} } {A(1 + z)^\xi}\label{44_3} \end{equation} it follows that \begin{equation} \begin{gathered} \rho _{_{DM}} = \rho _{_{DE}} A(1 + z)^\xi \\ \dot \rho _{_{DM}} = \dot \rho _{_{DE}} A(1 + z)^\xi - \xi \rho _{_{DE}} A(1 + z)^\xi H \label{44_4} \\ \end{gathered} \end{equation} Substitution of equations (\ref{44_2}) and (\ref{44_3}) into (\ref{44_4}) gives the following: $$ Q - 3H\rho _{_{DM}} = - (Q + 3H\rho _{_{DE}} (1 + w_{_{DE}} ))A(1 + z)^\xi - \xi \frac{\rho _{_{DM}}} {A(1 + z)^\xi}A(1 + z)^\xi H.$$ And one finally obtains: $$ Q = - 3H\frac{\frac{\xi } {3} + w_{_{DE}} } {1 + A(1 + z)^\xi }\rho _{_{DM}}.$$
Problem 14
Determine the statefinder $\{r,s\}$ (see Chapter Dark Energy) in the model of interacting dark energy and dark matter with the interaction intensity $Q=-3\alpha H$.
\[ r = 1 + \frac{9}{2}\frac{w}{1 + R}\left[ {1 + w - \frac{\alpha }{\rho _{_{DE} }} - \frac{\dot w}{3wH}} \right]; \] \[ s = 1 + w - \frac{\alpha }{\rho _{_{DE}}} - \frac{\dot w}{3wH}; \] \[ R = \frac{\rho _{_{DM}} }{\rho _{_{DE} }};\quad p_{_{DE}} = w\rho _{_{DE}}.\]
Problem 15
Consider a flat Universe filled with dark energy in the form of the Chaplygin gas ($p_{ch}=-A/\rho_{ch}$) and dark matter. Let the components interact with each other with intensity $Q=3\Gamma H\rho_{ch}$ ($\Gamma>0$). Show that for large $a$ ($a\to\infty$) holds $w_{ch}\equiv p_{ch}/\rho_{ch}<-1$, i.e. in such a model the Chaplygin gas behaves as the fantom energy.
The conservation equation for the Chaplygin gas component reads \[ \dot \rho_{ch} + 3H\left( { - \frac{A}{\rho _{ch}} + 1} \right)\rho _{ch} = - Q = - 3\Gamma H\rho _{ch} .\] The above equation has the following solution \[ \rho _{ch} = \sqrt {\frac{A}[[:Template:1 + \Gamma]] + Ca^{ - 6(\Gamma + 1)} }, \] where $C > 0$ is the integration constant. For large $a$ \[ \lim\limits_{a \to \infty } w_{ch} = - (\Gamma + 1) < - 1. \]
Problem 16
Interaction between dark matter and dark energy leads to non--conservation of matter, or equivalently, to scale dependence for the mass of particles that constitute the dark matter. Show that, within the framework of the model considered in problem, the relative change of particles mass per Hubble time equals the interaction constant.
et $\rho _{_{DM}} = m(a)n_{_{DM}}$. Using the result of problem \[ \rho _{_{DM}} = \rho _{_{DM0}} a^{ - 3} \exp \left( {\int {\delta d\alpha } } \right);\quad \alpha \equiv \ln a, \] one obtains \[ \frac{1}{m}\frac{dm}{d\ln a} = \frac{1}{m}\frac{dm}{Hdt} = \delta. \]
Problem 17
Consider a model of flat homogeneous and isotropic Universe filled with matter (baryon and dark), radiation and a negative pressure component (dark energy in the form of quintessence). Assuming that the baryon matter and radiation conserve separately and the dark components interact with each other, describe the dynamics of such a system.
Problem 18
Assume that the dark matter particles' mass $m_{DM}$ depends on a scalar field $\varphi$. Construct the model of interacting dark energy and dark matter in this case.
Use the standard definition for the dark matter density \begin{equation}\label{11_51_1} \rho _{_{DM}} = m_{_{DM}} (\varphi )n_{_{DM}}. \end{equation} The number density satisfies the equation \begin{equation}\label{11_51_2} \dot n_{_{DM}} + 3Hn_{_{DM}} = 0. \end{equation} Taking derivative over time in (\ref{11_51_1}) and using (\ref{11_51_2}), one obtains \[ \dot \rho _{_{DM}} + 3H\rho _{_{DM}} = \frac{1}{m_{_{DM}} (\varphi)}\frac{dm_{_{DM}} (\varphi )}{d\varphi }\dot \varphi \rho _{_{DM}}. \] In the case of mass independent from $\varphi $ it reproduces the usual equation for the energy density of dark matter particles \[ \dot \rho _{_{DM}} + 3H\rho _{_{DM}} = 0.\] As general covariance lead to conservation law for total energy of dark matter and the scalar field, one finally gets \[ \dot \rho _{_{DE}} + 3H(\rho _{_{DE}} + p_{_{DE}} ) = - \frac{1}{m_{_{DM}} (\varphi )}\frac{dm_{_{DM}}(\varphi )}{d\varphi }\dot \varphi \rho _{_{DM}}.\]
Problem 19
Find the equation of motion for the scalar field interacting with dark matter if its particles' mass depends on the scalar field.
Substitution of standard definitions of energy density and pressure of the scalar field into the conservation equation gives \[ \ddot \varphi + 3H\dot \varphi + \frac{\partial V(\varphi )}{\partial \varphi}= - \frac{1}{m_{_{DM}} (\varphi )}\frac{dm_{_{DM}} (\varphi)}{d\varphi }\rho _{_{DM}}.\]
Problem 20
Find the interaction $Q$ for the Universe, with interacting dark energy and dark matter, assuming that their densities' ratio takes the form $\rho_m/\rho_{DE}=f(a)$, where $f(a)$ is an arbitrary differentiable function of the scale factor.
\begin{equation}\label{eq66}\rho_m=\rho_{_{DE}}f(a)\end{equation} \begin{equation}\label{eq67}\rho_{_{DE}}=\frac{\rho_m}{f(a)},\end{equation} \begin{equation}\label{eq68}\dot{\rho}_m=\dot{\rho}_{_{DE}}f+\rho_{_{DE}}f^\prime \dot{a},\end{equation} \begin{equation}\label{eq69}\dot{\rho}_{_{DE}}=\frac{\dot{\rho}_m}{f}- \frac{\rho_m\dot{a}f^\prime}{f^2}, \end{equation} where the prime denotes derivative with respect to the scale factor. Substitution of the expressions \eqref{eq68} and \eqref{eq66} into the conservation equation for the dark matter gives the following: \begin{equation}\label{eq700} \dot{\rho}_{_{DE}}f+\rho_{_{DE}}f^\prime\dot{a}+3H\rho_{_{DE}}f=Q, \end{equation} Inserting into the latter the expression for $\dot{\rho}_{_{DE}}$, obtained from the conservation equation for the dark energy, one gets the following: \begin{equation}\label{eq70} Q=\frac{H\rho_{_{DE}}f}{1+f}\left(\frac{f^\prime a}{f}-3w_{_{DE}}\right). \end{equation} The first Friedman equation takes the form: \begin{equation}\label{eq701} \frac{3H^2}{8\pi G}=\rho_{_{DE}}+\rho_m=\rho_{cr}, \end{equation} where $\rho_{cr}$ is the critical density. Therefore one can rewrite that \begin{equation}\label{eq72} \Omega_{_{DE}}=\frac{\rho_{_{DE}}}{\rho_{cr}}=\frac{1}{1+f},\end{equation} \begin{equation}\label{eq730}\Omega_m=\frac{\rho_m}{\rho_{cr}}=\frac{f}{1+f}. \end{equation} And finally we obtain the expression for $Q$, by substitution of \eqref{eq730} into \eqref{eq70}: \begin{equation}\label{eq71} Q=H\rho_{_{DE}}\Omega_m\left(\frac{f^\prime a}{f}-3w_{_{DE}}\right) =H\rho_m\Omega_{_{DE}}\left(\frac{f^\prime a}{f}-3w_{_{DE}}\right). \end{equation}
Problem 21
Using the results of previous problem, find the quantity $E^2\equiv H^2/H_0^2$, which is necessary to test the cosmological models and to find restrictions on the cosmological parameters. Assume that $f(a)=f_0 a^\xi$, where $\xi$ is constant.
\begin{equation}\label{eq79}
f(a)=f_0\,a^\xi,
\end{equation}
where $\xi$ is constant; $f_0=f(a=1)=\frac{\rho_{m0}}{\rho_{_{DE0}}}
=\frac{\Omega_{m0}}{1-\Omega_{m0}}= \frac{1}{\Omega_{_{DE0}}}-1.$
From the conservation equation for both the densities one finds that
\begin{equation}\label{eq702}
\frac{d \ln\rho_{tot}}{d\ln a}=-3(1+w_{eff}),
\end{equation}
where
\begin{equation}\label{eq73}
w_{eff}=\frac{p_{tot}}{\rho_{tot}} =\frac{\rho_{_{DE}}w_{_{DE}}}{\rho_{_{DE}}+\rho_m} =\frac{w_{_{DE}}}{1+f}=\Omega_{_{DE}}w_{_{DE}},
\end{equation}
and therefore
\begin{equation}\label{eq74}
\frac{d \ln\rho_{tot}}{d\ln a}=-3(1+\Omega_{_{DE}}w_{_{DE}}).
\end{equation}
from the latter equation it follows that
\begin{equation}\label{eq75}
\rho_{tot}=Ca^{-3}\exp\left(-\int 3\Omega_{_{DE}}w_{_{DE}}\,d\ln a
\right)
\end{equation}
where $C$ is the integration constant, which can be determined from the condition that $\rho_{tot}(a=1)=\rho_{tot,0}=3H_0^2/(8\pi G)$.
Taking into account the equations (\ref{eq79}) and
(\ref{eq75}), and requiring that $\rho_{tot}(a=1)=\rho_{tot,0}$,
one determines the integration constant and finds that
\begin{equation}\label{eq80} \rho_{tot}=\rho_{tot,0}\,a^{-3}\left[\,\Omega_{m0}+
\left(1-\Omega_{m0}\right)a^\xi\,\right]^{-3w_{_X}/\,\xi}.
\end{equation}
Substitution of the latter expression into the Friedman equation gives the following:
\begin{equation}\label{eq81}
\begin{gathered}
E^2=\frac{H^2}{H_0^2}=a^{-3}\left[\,\Omega_{m0}+\left(1-\Omega_{m0}\right)a^\xi\,
\right]^{-3w_{_X}/\,\xi}\\
=(1+z)^3 \left[\,\Omega_{m0}+\left(1-\Omega_{m0}\right)
(1+z)^{-\xi}\,\right]^{-3w_{_X}/\,\xi}.
\end{gathered}
\end{equation}
Problem 22
In the Universe described in problems 1 and 2, calculate the distance module corresponding to the redshift's range $0.014\leq z\leq 1.6$ and find the quantity $E=H/H_0$.
The distance module is defined as \begin{equation}\label{test1} \mu_{th}(z_i)\equiv 5\log_{10}D_L(z_i)+\mu_0\,, \end{equation} where $\mu_0\equiv 42.38-5\log_{10}h$, and $h$ is the Hubble constant $H_0$ in units of $100 \,\mbox{km}/\mbox{s}/\mbox{Mpc}$. The photometric distance is defined by \begin{equation}\label{test2} D_L(z)=(1+z)\int_0^z \frac{d\tilde{z}}{E(\tilde{z})}\,, \end{equation} where $E\equiv H/H_0$. In the case $\frac{\rho_{m}}{\rho_{_{DE}}}=f_0a^\xi,$ one has the following \begin{equation} E^2=\frac{H^2}{H_0^2}=(1+z)^3 \left[\,\Omega_{m0}+\left(1-\Omega_{m0}\right) (1+z)^{-\xi}\,\right]^{-3w_{_X}/\,\xi}, \end{equation} and therefore $E\equiv H/H_0$ equals to \begin{equation} E=\frac{H}{H_0}=\sqrt{(1+z)^3 \left[\,\Omega_{m0}+\left(1-\Omega_{m0}\right) (1+z)^{-\xi}\,\right]^{-3w_{_X}/\,\xi}} \end{equation} Inserting the latter expression into \eqref{test2}, one recovers \eqref{test1}. It is useful to compare the obtained results with the observational data for the distance module [arXiv:0901.4804]. Figure presents the dependence of the distance module $\mu$ on the redshift $z$, solid line give theoretical predictions obtained in frame of the considered model, points give the results of the type Ia supernovae observations arXiv:0901.4804.
Problem 23
Consider a model of the Universe with interacting components, in which the scale factor dependence for one of them takes the form $\rho _{1} (a)=C_{1} a^{\alpha } +C_{2} a^{\beta }$, where $C_1$, $C_2$, $\alpha$ and $\beta$ are constants. Find the interaction $Q$.
\begin{equation} \label{eq10} {Q=(\alpha+3(1+w_1))HC_1a^\alpha+(\beta+3(1+w_1))HC_2a^\beta}. \end{equation}
Problem 24
In the model of the Universe considered above assume that $\rho_1=\rho_m$, $\rho_2=\rho_{DE}$ and $Q=\gamma H\rho_1$. Find the range of possible values of the interaction constant $\gamma$.
In the considered case $\rho_1=\rho_{m}$, $\rho_2=\rho_{_{DE}}$, and therefore $w_1=0$, so $ Q=\gamma H \rho_{1}$ can be rewritten as $Q=\gamma H\rho_{m}$ and the expressions for the energy densities take the form:
\begin{equation}\label{eq24}
\rho_{m}=\rho_{m0}a^{\gamma-3},
\end{equation}
\begin{equation}\label{eq25}
\rho_{_{DE}}=\rho_{_{DE0}}a^{-3(1+w_2)}-\frac{\gamma\rho_{m0}}{\gamma+3w_2}a^{\gamma-3},
\end{equation}
where $\rho_{_{DE0}}$ and $\rho_{m0}$ are constant. For $-1\leq w_2<-1/3$ the dark energy becomes the quintessence, and for $w_2<-1$ it is phantom energy. The case $\gamma=0$ corresponds to absence of interaction, which means that the dark matter and dark energy evolve independently.
As the dark matter density must decay during the expansion of the Universe, it follows from the equation \eqref{eq24} that $\gamma-3<0$. On the other hand the energy densities of dark matter and dark energy must be positive during all the evolution of Universe, thus $\frac{\gamma}{\gamma+3w_2}<0$, $\rho_{_{DE0}}-\frac{\gamma}{\gamma+3w_2}>0$. The condition $\frac{\gamma}{\gamma+3w_2}<0$ implies that $\gamma>0$ and $\gamma+3w_2<0$ or vice versa $\gamma<0$ and $\gamma+3w_2>0$. All other combinations of $\gamma$ and $w_2$ inevitably lead to the result that the energy densities become negative at some value of the scale factor in the process of the Universe evolution. it is worth noting also that if $\gamma<0$ and $\gamma+3w_2>0$, then one obtains $w_2>0$, which is impossible by definition. And finally the allowed range for variation of $\gamma$ is the following: \[0<\gamma<3.\]
Problem 25
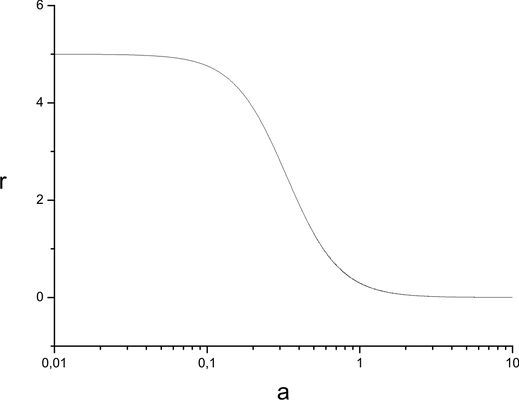
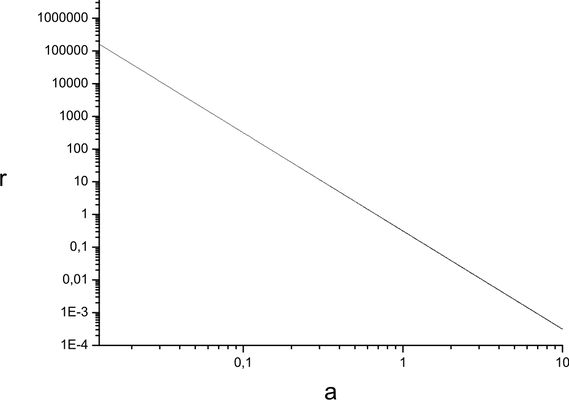
Show that in the model considered in problem 61 there is no coincidence problem.
On early stages of Universe evolution the dark energy density grows behaves as $\rho_{_{DE}}\simeq-\frac{\gamma \rho_{m0}}{\gamma+3w_2}a^{-3+\gamma}$ and therefore $r=\rho_{m}/\rho_{_{DE}}\simeq-(\gamma+3w_2/\gamma)$. On later stages of the evolution of Universe $r\rightarrow 0$, and it corresponds to the fact that the dark energy dominates over the dark matter. Thus the coincidence problem is partly solved in the considered model, because the densities ratio is constant on early stages of evolution of Universe (see Figure).
Problem 26
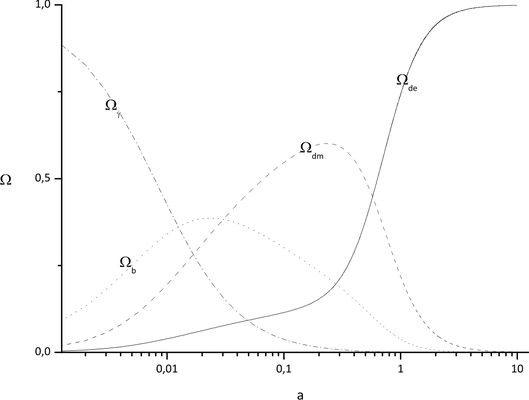
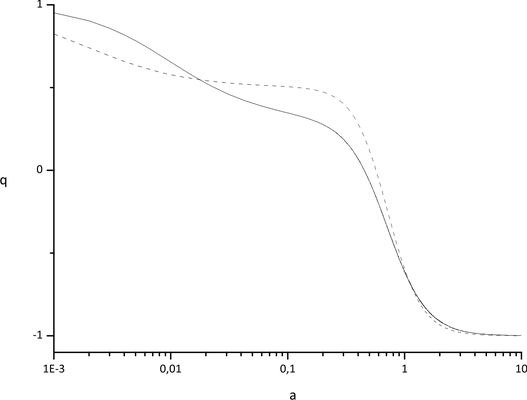
In the model of problem 61 find the scale factor's value $a_{eq}$ at the time when the dark matter density was equal to that of dark energy, and the scale factor's value $a_{ac}$ at the time when the Universe started to accelerate. Find the ranges of the state parameter $w_{DE}$ corresponding to the cases $a_{ac}<a_{eq}$ and $a_{ac}>a_{eq}$.
For the model under interest the equilibrium $r(a_{eq})=1$ between the dark matter and dark energy is possible under the following condition: \begin{equation}\label{eq26} a_{eq}=\left(\frac{\gamma+3w_2}{2\gamma+3w_2}\frac{\rho_{_{DE0}}}{\rho_{m0}}\right)^{1/(\gamma+3w_2)} \end{equation} Let us now find the expression for the scale factor at the moment of time when the accelerated expansion of Universe started. For that purpose one should set $\ddot{a}=0$ in the second friedman equation to obtain the following: \begin{equation}\label{eq27} a_{ac}=\left(\frac{(1+3w_2)(\gamma+3w_2)}{3w_2(\gamma-1)}\frac{\rho_{_{DE0}}}{\rho_{m0}}\right)^{1/(\gamma+3w_2)} \end{equation} It is easy to see that the two latter expressions do not coincide. One can see also that for $w_2<-2/3$ one gets $a_{ac}<a_{eq}$. It implies that the expansion of Universe already entered the accelerated phase, though the dark matter still dominates. For $-2/3<w_2<-1/3$ one has $a_{ac}>a_{eq}$, so the acceleration started when the dark energy already dominated. Figure show the dependencies of relative densities and deceleration parameter on the scale factor respectively. As can be seen from Figure, dynamics of Universe on late stages is indistinguishable from the SCM.
Non-linear Models
The interactions studied so far are linear in the sense that the interaction term in the individual energy balance equations is proportional to either dark matter density or to dark energy density or to a linear combination of both densities. Also from a physical point of view an interaction proportional to the product of dark components seems preferred: an interaction between two components should depend on the product of the abundances of the individual components, as, e.g., in chemical reactions. Moreover, such type of interaction looks much more attractive in comparison with the observations than the linear one. Below we investigate the dynamics for a simple two-component model with a number of non-linear interactions (F.Arevalo, A.Bacalhau and W. Zimdahl, arXiv: 1112.5095)
Problem 27
Let interaction term $Q$ is a non-linear function of the energy densities of the components and/or the total energy density. Motivated by the structure
\[\rho_{DM}=\frac{r}{1+r}\rho,\ \rho_{DE}=\frac{1}{1+r}\rho,\]
\[\rho\equiv\rho_{DM}+\rho_{DE},\ r\equiv\frac{\rho_{DM}}{\rho_{DE}},\]
consider the ansatz
\[Q=3H\gamma\rho^m r^n(1+r)^s,\]
where $\gamma$ is a positive coupling constant. Show that
1) for $s=-m$ interaction term is proportional to a power of products of the densities of the components;
2) for $(m,n,s)=(1,1,-1)$ and $(m,n,s)=(1,0,-1)$ the linear case is reproduced.
Problem 28
Find analytical solution of non-linear interaction model covered by the ansatz of previous problem for $(m,n,s)=(1,1,-2)$, \(Q=3H\gamma\rho_{DE}\rho_{DM}/\rho\).
In such a case equation for the ratio $r=\rho_{DM}/\rho_{DE}$ reduces to \[r'=r(w+\gamma)\] where $w=p_{DE}/\rho_{DE}$, the prime denotes the derivative with respect to $\ln a^3$. The solution of this equation is \[r=r_0a^{3(w+\gamma)}.\] Substitution of the latter solution into \[\rho'=-\left(1+\frac{w}{1+r}\right)\rho\] gives the total energy density \[\rho=\rho_0a^{-3(1+w)}\left[\frac{1+r_0a^{3(w+\gamma)}}{1+r_0}\right]^\frac{w}{w+\gamma}.\] The densities of the components are \[\rho_{DM}=\rho_{DM0}a^{-3(1-\gamma)}\left[\frac{1+r_0a^{3(w+\gamma)}}{1+r_0}\right]^{-\frac{\gamma}{w+\gamma}},\] \[\rho_{DE}=\rho_{DE0}a^{-3(1+w)}\left[\frac{1+r_0a^{3(w+\gamma)}}{1+r_0}\right]^{-\frac{\gamma}{w+\gamma}},\] \[\rho_{DM0}=\frac{r_0}{1+r_0}\rho_0,\ \rho_{DM0}=\frac{1}{1+r_0}\rho_0.\]
Problem 29
Find analytical solution of non-linear interaction model for $(m,n,s)=(1,2,-2)$, \(Q=3H\gamma\rho_{DM}^2/\rho\).
Proceeding like in the previous problem, one finds: \[r=r_0\frac{w}{(w-\gamma r_0)a^{-3w}-\gamma r_0},\] \[\rho=\rho_0a^{-3\left(1-\frac{w\gamma}{w-\gamma}\right)}\left[\frac{(w+\gamma r_0)a^{-3w}+r_0(w-\gamma)}{w(1+r_0)}\right]^\frac{w}{w-\gamma}.\]
Problem 30
Find analytical solution of non-linear interaction model for $(m,n,s)=(1,0,-2)$, \(Q=3H\gamma\rho_{DE}^2/\rho\).
For $w<0$ the solution reads: \[r=\left(r_0-\frac{\gamma}{|w|}\right)a^{-3|w|}+\frac{\gamma}{|w|},\] \[\rho=\rho_0a^{-3\left(1-\frac{|w|^2}{|w|+\gamma}\right)}\left[\frac{|w|+\gamma (|w|r_0-\gamma)a^{-3|w|}}{|w|(1+r_0)}\right]^\frac{|w|}{|w|+\gamma}.\]
The Chaplygin Gas
Any fundamental science shows an obvious tendency to decrease number of the fundamental substances. The well-known examples are transition from chemical elements to nucleons and electrons, and then from baryons and mesons - to quarks. Cosmology manifests an intention to develop a unified model for dark energy and dark matter. The observed transition from the matter domination to that of dark energy makes it attractive to introduce a dynamical substance which would mimic properties of matter in early Universe and possess the negative pressure to provide the accelerated expansion in the present epoch. The Chaplygin gas represents the simplest substance with the required properties. Its equation of state is postulated to be: \[p=-\frac{A}{\rho}, \ A>0.\]
Problem 31
Find the scale factor dependence for the density of the Chaplygin gas.
Substitute the Chaplygin gas state equation into the conservation equation for the expanding Universe and separate the variables to obtain the following: $$\frac{d\rho}{\rho - \frac{A}{\rho }} = - 3\frac{da}{a}.$$ Integrate the latter equation with the initial conditions $\rho \left( {a_0 } \right) = \rho '$ and introduce the notion $\rho '^2 - A = \rho _0^2 $ to get the require dependence: \[ \rho \left( a \right) = \sqrt {A + \rho _0^2 \left( {\frac{a_0}{a}} \right)^6 } \]
Problem 32
Show that in the early Universe the Chaplygin gas behaves as matter with zero pressure, and at later times---as the cosmological constant.
Use the result of the previous problem \[ \rho \left( a \right) = \sqrt {A + \rho _0^2 \left( {\frac{a_0 }{a}} \right)^6 } \] For early Universe $a_0/a\gg 1$ and $$ A \ll \rho _0^2 \left( \frac{a_0 }{a} \right)^6 ,$$ then $\rho \left( a \right) \approx \rho _0 \left( \frac{a_0 }{a} \right)^3$, which corresponds to matter with zero pressure. In later stages of evolution of Universe $a_0 /a \ll 1$ and $A \ll \rho _0^2 \left(\frac{a_0 }{a} \right)^6$, so that $\rho \left( a \right) \approx A = const $. The latter equation of state corresponds to the cosmological constant.
Problem 33
Find the range of the energy density $\rho_{ch}$ corresponding to the accelerated expansion of the Universe filled with dark energy in the form of Chaplygin gas with pressure $p=-A/\rho_{ch}$ and non--relativistic matter with density $\rho_m$.
The condition for the accelerated expansion reads $$ \rho + 3p < 0,\;\rho > 0; $$ $$ \rho + 3p = \rho _m + \rho _{ch} + 3p_{ch} = \rho _m + \rho _{ch} - \frac{3A}{\rho _{ch} }; $$ $$ 0 < \rho _{ch} < \frac{ - \rho _m + \sqrt {\rho _m^2 + 12A} } 2 $$
Problem 34
Show that the sound speed in the Chaplygin gas in the late Universe is close to the light speed.
he sound speed in the Chaplygin gas (see the problems 1, 2) equals to \[c_{s}^{2}=\frac{dp}{d\rho }=\frac{A}{{{\rho }^{2}}}=\frac{A{{a}^{6}}}{B+A{{a}^{6}}}=\left\{ \begin{aligned} & 0\quad a\ll 1 \\ & 1\quad a\sim 1 \\ \end{aligned} \right.\] High sound speeds $\left( {{c}_{s}}\sim c \right)$ in late Universe $\left( a\sim 1 \right)$ represent the main defeat of the model. This problem was partially fixed in the so-called generalized Chaplygin gas models (see the problem \ref{DE90}).
Problem 35
Show that the sound speed in the Chaplygin gas behaves as $c_s\propto t^2$ in the matter--dominated epoch.
$c_s = \sqrt {\frac{dp_{ch}}{d\rho _{ch} }} = \frac{\sqrt A }{\rho _{ch} } \propto t^2$
Problem 36
Show that the cosmological solution corresponding to the Chaplygin gas can be obtained in the quintessence model.
Let the scalar field energy density equals to that of the Chaplygin gas \begin{equation} \label{DE78n_1} \rho_{\varphi}=\frac{1}{2}{{\dot{\varphi }}^{2}}+V(\varphi )=\sqrt{A+\frac{B}{{{a}^{6}}}}, \end{equation} then for ${{p}_{\varphi }}=-A/{{\rho }_{\varphi }}$ one finds \begin{equation} \label{DE78n_2} p_{\varphi }=\frac{1}{2}\dot{\varphi}^2-V(\varphi )=-\frac{A}{\sqrt{A+\frac{B}{a^6}}}. \end{equation} It follows from (\ref{DE78n_1}), (\ref{DE78n_2}) that \begin{equation} \label{DE78n_3} {{\dot{\varphi }}^{2}}=\frac{B}{{a^6}\sqrt{A+\frac B{a^6}}}\\ \end{equation} \begin{equation} V(\varphi)=\frac{2{{a}^{6}}\left( A+\frac{B}{{{a}^{6}}} \right)-B}{2{{a}^{6}}\sqrt{A+\frac{B}{{{a}^{6}}}}}. \label{DE78n_4} \end{equation} Using the first Friedmann equation, the relation (\ref{DE78n_3}) (for the flat case in the units $8\pi G=1$) can be presented in the following form: \begin{equation} \label{DE78n_5} \frac{d\varphi}{da}=\frac{\sqrt{B}}{a{{\left( A{{a}^{6}}+B \right)}^{1/2}}}. \end{equation} The latter relation can be easily integrated to give the following result: \begin{equation} \label{DE78n_6} {{a}^{6}}=\frac{4B\exp (6\varphi )}{A{{\left( 1-\exp (6\varphi ) \right)}^{2}}} \end{equation} Substitution of (\ref{DE78n_6}) into (\ref{DE78n_4}) gives the following simple expression for the scalar field potential: \begin{equation} \label{DE78n_7} V(\varphi )=\frac{1}{2}\sqrt{A}\left[ \cosh (3\varphi )+\frac{1}{\cosh (3\varphi )}. \right] \end{equation} The latter potential does not depend on the integration constant $B$, it is determined only by the constant $A$, which enters the state equation of the Chaplygin gas.
Problem 37
Find the dependence of density on the scale factor in the generalized Chaplygin gas model with state equation \[p=-\frac{A}{\rho^\alpha},\ (A>0,\ \alpha>0.)\]
$$ \rho _{ch}^{(gen)} = \left[ {A + Ba^{ - 3(1 + \alpha )} } \right]^{\frac 1 {1 + \alpha }} $$ where $B > 0$ is the integration constant.
Problem 38
In the generalized Chaplygin gas model (see previous problem) find the state equation parameter $w$.
As is known, $w = \frac p{\rho }$. Transform the explicit solution $\rho (a)$, obtained in the previous problem $$ \rho = \left[ {A + Ba^{ - 3(1 + \alpha )} } \right] = \rho _0 \left[ {A^* + (1 - A^* )a^{ - 3(1 + \alpha )} } \right]^{\frac 1{1 + \alpha }} $$ where $A^* \equiv A\rho _0^{ - (1 + \alpha )} ;\;a_0 = 1$. Use the following $p = - \frac A {\rho ^\alpha}\quad \left( {A > 0,\alpha> 0} \right), $ to obtain $$ w = - \left[ {1 + \frac{1 - A^* }{A^* }a^{ - 3(1 + \alpha )} } \right]^{ - 1}. $$ One makes sure again that in early Universe (small values of the scale factor) the generalized Chaplygin gas mimics the non-relativistic matter $w \simeq 0$, and at later epoch---as the cosmological constant $w \simeq - 1$.
Problem 39
Determine the sound speed in the generalized Chaplygin gas model (see problem). Can it exceed the speed of light?
$$ c_s^2 = \frac{dp}{d\rho } = - \alpha w $$ For the values $\alpha > 1$ on later stages of the evolution of Universe this quantity can exceed the lightspeed, because $w \simeq - 1$ in that case.
Problem 40
Let us present the energy density in the generalized Chaplygin gas model of problem in the form of the sum $\rho_{ch}^{(gen)} = \rho_{DM}+\rho_{DE}$, where $\rho_{DM}$ is the component with the properties of non-relativistic mater ($p_{DM}=0$) and $\rho_{DE}$ is the component with the properties of dark energy described by the state equation $p_{DE}=w_{DE}\rho_{DE}$. Find the restriction on the model's parameter $w_{DE}$.
$$ w = {\frac{p_{ch}^{(gen)} }{\rho _{ch}^{(gen)} }} = {\frac{p_{DE} } {\rho _{DE} + \rho _{DM} }} = {\frac{w_{DE} \rho _{DE} }{\rho _{DE} + \rho _{DM}}} $$ Using the explicit expression for $\rho _{ch}^{(gen)} $, obtained in the previous problem, and the model definition $p_{ch}^{(gen)} $ $$ \rho _{ch}^{(gen)} = \left[ {A + B(1 + z)^{3(1 + \alpha )} } \right]^{{\frac 1{1 + \alpha }}} ; $$ $$ p_{ch}^{(gen)} = \frac A {\left[ {A + B(1 + z)^{3(1 + \alpha )} } \right]^{{\frac{\alpha}{1 + \alpha }} }} $$ one finds $$ \rho _{DE}^{(gen)} = {\frac{\rho _{DM}^{(gen)} }{1 + w_{DE} \left[ {1 + {\frac B A}(1 + z)^{3(1 + \alpha )} } \right]}} $$ The requirement $\rho _{DE}^{(gen)} > 0$ leads to the condition $w_{DE} \le 0$ for early Universe$\left( {z \gg 1} \right)$ and $w_{DE} \le - 1$ for future $\left( {z = - 1} \right)$. Therefore the condition $w_{DE} \le - 1$ garantees the possibility to describe whole history of universe in frames of the chosen model.
Problem 41
Find the dependence of density on scale factor for the Chaplygin gas model with the state equation \[ p = \left( {\gamma - 1} \right)\rho - \frac{A}{\rho ^\alpha };\quad 0 \le \alpha \le 1 \] (the so-called modified Chaplygin gas).
$$ \rho = \left[ {{\frac A {\gamma} } + {\frac C {a^{3\gamma (1 + \alpha )} }}} \right]^{{\frac 1{1 + \alpha }}} ;\quad $$ where $C$ is the integration constant. The latter solution can be rewritten in the following form $$\rho = \rho _0 \left[ {A^* + {\frac{1 - A^* } {a^{3\gamma (1 + \alpha )} }}} \right]^{{\frac 1 {1 + \alpha }}};\quad A^* = {\frac A {\gamma} }\rho _0^{ - (\alpha + 1)} ;\quad a_0 = 1.$$ For $\gamma = 1$ it reproduces the dependence $\rho (a)$ for the generalized model of the Chaplygin gas (see the problem of the present Chapter), and for $\gamma = 1,\;\alpha = 1$---for the usual Chaplygin gas model (see the problem of the present Chapter).
Problem 42
Construct the effective potential for the Chaplygin gas considering it as a scalar field. Do the same for the generalized Chaplygin gas (see problem) and the modified Chaplygin gas of the previous problem.
Problem 43
Show that for the Chaplygin gas model the line $w=-1$ cannot be crossed.
Equation of state for the Chaplygin gas is given by \[p=-\frac A\rho,\ A>0.\] As shown earlier \[\rho=\sqrt{A+Ca^{-6}},\] where $C$ is a real positive constant. Consequently, \[w=\frac p\rho=-\frac{A}{\rho^2}=-\frac{A}{A+Ca^{-6}}.\] We have $-1<w<0$ for $a\in(0,\infty)$, hence $w=-1$ cannot be crossed in this model.
Problem 44
Show that for the generalized Chaplygin gas model the line $w=-1$ cannot be crossed.
Equation of state of the generalized Chaplygin gas is given by \[p=-\frac{A}{\rho^\alpha},\ A>0,\ \alpha\ge0.\] Using the conservation equation, find density in terms of the scale factor \[\rho=\left[A_s+\frac{1-A_s}{a^{3(\alpha+1)}}\right]^{\frac{1}{1+\alpha}},\ A_s\equiv\frac{A}{\rho_0^{1+\alpha}}.\] The observations favor $0<A_s<1$. Then the state equation parameter of the generalized Chaplygin gas model is \[w=-A_s\left(\frac{\rho_0}{\rho}\right)^{1+\alpha}=-\frac{A_s a^{3(1+\alpha)}}{1-A_s+A_s a^{3(1+\alpha)}}.\] It is easy to see that with the restriction $A_s>0$ one obtains \[-1<w<0.\] Therefore such model excludes phantom region $w<-1$.
Universe as the Dynamical System
The Universe described by the Friedman equations can be treated as an autonomous dynamical system. Its behavior is determined by the system of differential equations of the form: \[\dot{\vec{x}}=\vec{f}(\vec{x}).\] To study dynamics of the system it is of crucial importance to find the so-called critical points $\vec{x}^*$ defined by the following condition: \[\vec{f}(\vec{x}^*)=0.\] In order to study the stability of the critical points, we expand around them: \[\vec{x}=\vec{x}^*+\vec{u},\ \dot{\vec{u}}=\vec{f}'(\vec{x}^*)\vec{u}+\vec{g}(\vec{x}).\] Here $\vec{g}(\vec{x})/||x||\to0$ as $\vec{x}\to\vec{x}^*$, and \[f'_{ij}(\vec{x}^*)\hat M(\vec{x}^*)=\frac{\partial f_i}{\partial x_j}(\vec{x}^*)\] is constant non-singular stability matrix, whose eigenvalues encode the behavior of the dynamical system near the critical point. The eigenvalues are just the roots of the equation \[\det|\hat M -\lambda \hat I|=0\] We yet limit ourself to two-dimensional case. If the solutions are non-degenerate and real, they describe a stable node for $\lambda_{\pm}<0$ an unstable node for $\lambda_{\pm}<0$ and a saddle if $\lambda_{+}$ and $\lambda_{-}$ have different signs. For complex eigenvalues $\lambda_{\pm}=\alpha\pm i\beta$, it is the sign of $\alpha$ that determines the character of the critical point. For $\alpha=0$ the critical point is a center, for $\alpha<0$ it is a stable focus and for $\alpha>0$ it is an unstable focus.
Inspired by Yi Zhang, Hui Li, arXiv:1003.2788
Problem 45
Assume that there are two components in the Universe: background matter and the dark energy. Obtain equations of motion for relative densities of both components.
The background matter is assumed to be described by a perfect fluid with barotropic equation of state \begin{equation}\label{DAMA_72_1} \rho'_m+3(1+w_m)\rho_m=0, \end{equation} where $\rho_m$ is the energy density of the background matter, a prime denotes the derivative with respect to $N=\ln a$, and $-1<w_m<1$. In particular, $w_m=0$ and $w_m=1/3$ correspond to dust matter and radiation, respectively. And for the dark energy component \begin{equation}\label{DAMA_72_2} \rho'_{DE}+3(1+w_{DE})\rho_{DE}=0, \end{equation} where $\rho_{DE}$ is the energy density of the dark energy for which $w_{DE}=p_{DE}/\rho_{DE}$. Friedmann equations for the whole system read \begin{equation}\label{DAMA_72_3} \begin{array}{l} H^2=\frac{\rho_{tot}}{3m^2_{Pl}}=\frac{1}{3m^2_{Pl}}(\rho_m+\rho_{DE}),\\ \dot H=-\frac{1}{2m^2_{Pl}}(\rho_{tot}+p_{tot})=-\frac{(1+w_{tot})\rho_{tot}}{2m^2_{Pl}},\\ w_{tot}=\frac{\frac{\Omega_m}{\Omega_{DE}}w_m+w_{DE}}{1+\frac{\Omega_m}{\Omega_{DE}}},\\ \Omega_i\equiv\frac{\rho_i}{3m^2_{Pl}H^2}. \end{array} \end{equation} Combining (\ref{DAMA_72_1})-(\ref{DAMA_72_3}) we can get the equations of motion for dynamical variables $\Omega_i$ \[\Omega'_m=3f_{ni}\Omega_m\Omega_{DE}\] \[\Omega'_{DE}=-3f_{ni}\Omega_m\Omega_{DE}\] where $f_{ni}=w_{DE}-w_m$. The index $ni$ means there is no interaction between the background matter and the dark energy.
Problem 46
Find fixed points for the dynamical system considered in the previous problem and analyze their stability.
The fixed points are $(\Omega_m,\Omega_{DE})=\{(1,0),(0,1)\}$. The stability matrix reads: \[\hat M=3f_{ni}\left( \begin{array}{lr} \Omega_{DE} & \Omega_m\\ -\Omega_{DE} & -\Omega_m \end{array} \right)\] Let the dark energy is realized in form of the cosmological constant, and matter---in form of dust $w_m=0$ or radiation $w_m=1/3$. In both cases $f_m<0$. For the critical point $(\Omega_m,\Omega_{DE})=(1,0)$ one obtains $\lambda_\pm=\{(0,1)\}$ and the considered critical point is unstable. Addition to the Universe of some portion of dark energy in form of the cosmological constant makes it evolve from the state $(\Omega_m,\Omega_{DE})=(1,0)$ into the state $(\Omega_m,\Omega_{DE})=(0,1)$. For the critical point $(\Omega_m,\Omega_{DE})=(0,1)$ one has $\lambda_\pm=\{(0,-1)\}$ and therefore the considered critical point is stable: if the Universe, filled by the cosmological constant, is perturbed by some portion of matter, then its relative density will drop to zero due to the expansion of Universe.
Problem 47
Find critical points for the model of interacting dark components with $Q=-3H\Pi$.
The considered dynamical system is described by the equations: \[\rho'=-\left(1+\frac{w}{1+r}\right)\rho,\ r\equiv\frac{\rho_{DM}}{\rho_{DE}},\] \[r'=\left[w-\frac{(1+r)^2}{r\rho}\Pi\right]r,\ \rho\equiv\rho_{DE}+\rho_{DM}.\] The condition \(\rho'=0\) provides the critical point \[r_c=-1-w.\] (We disregard the critical points with $r_c=\rho_c=0$ and the unphysical $r_c=-1,\,\rho_c=0$.) Consequently, for positive values of $r$, the existence of a critical point requires $w<-1$, i.e. dark energy of phantom type. This conclusion does not depend on the interaction. The condition $r'=0$ provides \[\rho_c=-\frac{w}{1+w}\Pi_c.\]
Problem 48
Show that for the model considered in the previous problem, independently from the specific interaction, the existence of the critical points $r_c$ and $\rho_c$ requires a transfer from dark energy to dark matter.
Since $w<-1$, a positive stationary energy density $\rho_c$ requires $\Pi_c<0$, equivalent to $Q_c>0$.
Problem 49
Find eigenvalues of the stability matrix for the model of Universe considered in the problems 1 and 2.
Recall that in the case $Q\propto H$ the energy balance equation is independent from $H$, thus phase space of such coupling model is two-dimensional. Then the dynamics of the two-component system is given by \[\rho'=-\left(1+\frac{w}{1+r}\right)\rho,\] \[r'=-\left[w-\frac{(1+r)^2}{r\rho}\Pi\right]r,\ \rho=\rho_{DE}+\rho_{DM}.\] Here the prime denotes derivative with respect to $\ln a^3$. Solution of the equation $\det|\hat M-\lambda\hat I|=0$ for the eigenvalues $\lambda$ of the stability matrix leads to the following equation: \[\lambda^2+\left[2+w-w(1+w)\frac{\partial_r \Pi}{\Pi}\right]\lambda+(1+w+w\partial_\rho\Pi)=0.\] This equation has the following solutions \[\lambda_\pm=\frac12\left\{\left[w(1+w)\frac{\partial_r \Pi}{\Pi}-(2+w)\right] \right.\] \[\left.\pm\sqrt{\left(2+w-w(1+w)\frac{\partial_r \Pi}{\Pi}\right)^2-4(1+w+w\partial_\rho\Pi)}\right\}.\]
Problem 50
Find eigenvalues of the stability matrix under assumption that $Q=3H\gamma\rho^mr^n(1+r)^s$ (see problem).
In that case the eigenvalues equal to the following: \[\lambda_\pm=-\frac12\left\{[2=s+(1+n+s)w]\mp\sqrt{2+s+(1+n+s)^2+4(m-1)(1+w)}\right\}.\]
Problem 51
Classify critical points for the model of interacting dark components considered in the previous problem.
For $m\ne1$ the general classification provides us with the following set of critical points:
1. Stable node for $m>1$ and \[s<\frac{2+(1+n)w}{1+w}-2\sqrt{\frac{1-m}{1+w}};\]
2. Unstable node for $m>1$ and \[s>\frac{2+(1+n)w}{1+w}+2\sqrt{\frac{1-m}{1+w}};\]
3. Saddle for $m<1$, arbitrary $n$ and $s$;
4. Center for $m>1$ and $2+s+(1+n+s)w=0$ for $n>1$;
5. Stable focus for $m>1$ and $2+s+(1+n+s)w>0$;
6. Unstable focus for $m>1$ and $2+s+(1+n+s)w<0$.