Observational Evidence of the Dark matter Existence
Problem 1
Analyze the problem of a small satellite galaxy moving in the gravitational field of a large galaxy (the problem of non-decreasing behavior of the rotational curves.)
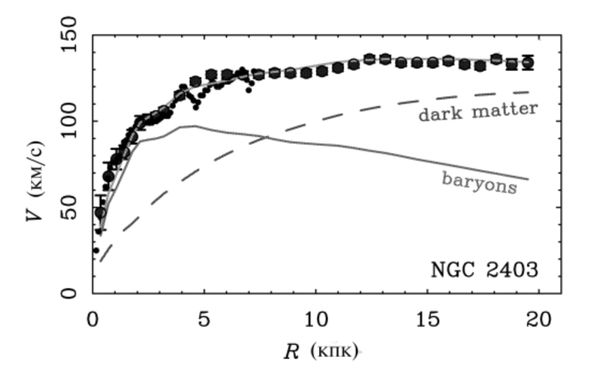
Many galaxies have several small satellite galaxies. For the latter the second Newton law reads: \[G\frac{mM(r)}{r^{2} } =\frac{mv^2}{r} \] For the rotation velocity one then obtains \[v(r)=\sqrt{\frac{GM(r)}{r} } \] where $M(r)$ is the total mass of the matter inside the sphere of radius $r$. In the spherically symmetric case the effect of the outside mass vanishes, and it follows that \[M(r)=\bar{\rho }\frac{4}{3} \pi r^{3} \Rightarrow v(r)=\sqrt{\frac{4}{3} \pi G\bar{\rho }r^{2} } \sim r,\] where $\bar{\rho }$ is the distribution of the mass $M.$ Thus linear growth of the rotation velocity with the galactocentric radius is expected in the inner part of the galaxy. In the outer region of the galaxy the dependence of the rotation velocity on the radius corresponds to the case of point mass in the center of the galaxy: \[v(r)\sim 1/\sqrt{r} \] The rotation velocity $v(r)$ can be in particular determined by the measured Doppler shift in the emission spectrum of the corresponding satellite galaxies. The behavior of the observed rotation curves measured for some thousands galaxies does not show the expected decrease $v(r)$ with radius growing. A pronounced approximate constance of $v(r)$ is observed instead for large radii (See Figure). This fact implies that the mass $M(r)$ must increase with the radius growing: $M(r)\sim r$. Then one can conclude that mass of the central is far from being exhausted by the one contained in the visible volume: it is distributed instead in much larger region. Unlike the stars, the latter additional mass does not emit light (it is invisible on pictures), but creates considerable gravity force, additional to that of the visible stars. That is how the concept of the hidden mass originates.
Problem 2
What radial dependence of the density of a spherically symmetric galactic halo corresponds to the constant velocity of satellite galaxies?
\[v(r)=\sqrt{\frac{GM(r)}{r} } \] $$M(r)=4\pi\int r^2 \rho(r)dr$$ If $\rho(r)\sim 1/r^2$ then $M(r)\sim r $ and $v(r)=const.$
Problem 3
We have noted above that outside the optically observed range of a galactic disk the rotation curves of the dwarf satellite galaxies do not depend on the galacto-centric distance (the flatness of the rotational curves). External regions of the galaxies are mostly filled by cold neutral hydrogen. Evidently the rotation velocity of the gas gives important information about the mass distribution in the galaxy. How can one measure that velocity?
One should use a radiotelescope to observe the radiation with the wavelength equal to $21$ cm, which corresponds to the superfine splitting generated by spin interaction between proton and electron in the hydrogen atom. Rotation of the hydrogen leads to Doppler shift of the spectral line. Magnitude of the shift allows to estimate the rotation velocity of the neutral hydrogen, which remains constant far beyond the visible size of the galaxy in absolute agreement with rotation velocities of the dwarf satellite galaxies. Note that the best position to observe the Doppler shift is aside in plane of the galaxy.
Problem 4
Using the virial theorem, express the mass of a galaxy cluster through the observed quantities---the average velocity of galaxies in the cluster and its size. Estimate the mass of the Coma cluster (Berenice's hair) for $R\approx10^{23}m$, $\langle v^2\rangle^{1/2}\approx2\cdot10^6m/s$.
If a system undergoes finite motion and its potential energy is uniform function of the coordinates, then time averaged values of kinetic and potential energies are related by the virial theorem. It can be used to estimate the matter density in the galactic clusters. If the potential energy $U$ is uniform of order $k$, then
\[2\left\langle T\right\rangle =k\left\langle U\right\rangle \]
For gravitational interaction $k=-1$, so
\[2\left\langle T\right\rangle =-\left\langle U\right\rangle \]
Average kinetic energy for a cluster of $N$ galaxies equals to
\[\left\langle T\right\rangle =N\left\langle mv^{2} \right\rangle /2=Nm\left\langle v^{2} \right\rangle/2 =\frac{M\left\langle v^{2} \right\rangle }{2} \]
Average potential energy of interaction for $N$ pairs of galaxies
\[-G\frac{N(N-1)}{2\left\langle r\right\rangle } m^{2} \approx -G\frac{(Nm)^{2} }{2\left\langle r\right\rangle } =-G\frac{M^{2} }{2\left\langle r\right\rangle } \]
From the virial theorem if follows that
\[M\left\langle v^{2} \right\rangle =G\frac{M^{2} }{2\left\langle r\right\rangle }. \]
and then
\[M\approx \frac{2\left\langle r\right\rangle \left\langle v^{2} \right\rangle }{G}.\]
Measurements of average distance and average velocity squared give value of the dynamical mass that is two orders of magnitude higher than the mass obtained from the galaxies luminosity analysis. This fact can be interpreted as one more evidence in favor of existence of the dark matter.
The above given arguing has some weak points. The viral equation is valid only for averaging over long time period, when closed systems are in equilibrium state. The galactic clusters are not closed systems: they interact with each other. Moreover, it is unclear whether they already achieved the equilibrium.
Problem 5
Show that the age of the matter--dominated Universe contradicts observations.
Problem 6
A galaxy has the visible mass of $10^{11}M_\odot$ and a horizontal rotation curve up to distance of $30kpc$ at velocity $250km/s$. What is the ration What is the dark to visible mass ratio in the galaxy?
Condition of equilibrium of the satellite galaxy reads: $$ \frac{G(M_{_{DM}}+M_b)}{R^2}=\frac{v^2}{R}, $$ where $M_{_{DM}}$ is the dark matter mass (the hidden mass), $R = 30 \mbox{ kpc},$ $M_b = 10^{11} M_ \odot.$ Then one obtains $$ \frac{M_{_{DM}}}{M_b} = \frac{Rv^2}{GM_b} -1\approx 3,4. $$