Technical warm-up
Uniformly accelerated observer, Rindler metric
Einstein's equivalence principle states that locally a gravitational field cannot be distinguished from a non-inertial frame of reference. Therefore a number of effects of General Relativity, such as time dilation in a gravitational field and formation of horizons, can be studied in the frame of Special Theory of Relativity when considering uniformly accelerated observers.
Problem 1: a particle in homogeneous electric field
Derive the equation of motion $x(t)$ of a charged particle in Minkowski space in a uniform electric field without initial velocity. Show that its acceleration is constant.
The particle's equation of motion is $\dot{p}=eE=const$, so on choosing conveniently the zero point of time, we have $p(t)=eEt$. Then energy is \[\varepsilon(t)=\sqrt{p^{2}c^{2}+m^{2}c^{4}}= \sqrt{\mu^{2}+\tilde{t}^{2}},\quad\text{where}\; \mu=mc^2,\;\tilde{t}=eEct.\] As $p=\varepsilon v/c^{2}$, for velocity we get \[\beta(t)\equiv \frac{v(t)}{c}=\frac{cp}{\varepsilon}= \frac{\tilde{t}}{\sqrt{\mu^2+\tilde{t}^2}}.\] Integrating and restoring initial conditions $(t_{0},x_{0})$, we obtain \[(x+\rho-x_{0})^{2}-c^{2}(t-t_{0})^{2}=\rho^{2}, \qquad\mbox{where}\quad \rho=\frac{mc^{2}}{eE}.\] This is a hyperbola branch $x>0$, with asymptotes on the light cone, symmetry axis $OX$ and center $t=t_{0}$, $x=x_{0}-\rho$. Now calculate the $4$-acceleration of the particle: from $\dot{p}^{1}=\dot{p}=eE$, and $\dot{p}^{0}=\dot{\varepsilon}/c=eEv/c$ we obtain \[a_{\mu}a^{\mu}= \left(\frac{du^0}{ds}\right)^2- \left(\frac{du^1}{ds}\right)^2= \gamma^{2} \left[(\dot{u}^{0})^{2}-(\dot{u}^{1})^{2}\right]= \frac{\gamma^{2}}{(mc)^{2}} \left[\frac{\dot{\varepsilon}^{2}}{c^{2}} -\dot{p}^{2}\right]= -\frac{a^{2}}{c^{2}}.\] It is instructive to show that this acceleration is also the acceleration in the momentarily comoving frame. The latter is derived using the velocity composition law $v'=\frac{v+u}{1+vu}$, the expression for the proper time interval $d\tau=\gamma^{-1}dt$, and relation $\dot{p}=\gamma^{3}m\dot{v}$: \[a=\left.\frac{dv'}{d\tau}\right|_{v'=0}= \gamma\left.\frac{d}{dt}\frac{u+v}{1+uv} \right|_{u+v=0}=\gamma \frac{dv/dt}{1-\beta^{2}}= \gamma^{3}\dot{v}=\frac{\dot{p}}{m}= \frac{eE}{m}=\frac{c^{2}}{\rho}.\]
Problem 2: (unexpected?) horizons!
What region of spacetime is unobservable for such an accelerated observer? In what region is this observer unobservable?
The uniformly accelerated observer will never observe the region \[D_{+}=\big\{(x,t)\;|\;c(t-t_{0})>(x-x_{0}+\rho)\big\},\] as light from there will never reach him. That means the considered observer will never see the part of evolution of any fixed or uniformly moving particle, starting from some moment of time \[t_{h}(x)=t_{0}+\tfrac{1}{c}(x-x_{0}+\rho),\] in which it enters $D_+$ by crossing its boundary, the future event horizon. As the observer is constantly accelerating, its proper time slows down, so from his point of view the particle will asymptotically approach the $x$ coordinate, never reaching it. He will only see the rest of the particle's worldline if he stops accelerating (this always happens, though, in a realistic situation). Likewise, an observer in \[D_{-}=\big\{(x,t)\;|\;c(t-t_{0})<-(x-x_{0}+\rho)\big\}\] will never receive light emitted by the uniformly accelerating particle. That is, any uniformly moving observer only sees the accelerating particle starting from some finite time. Before that the particle lies beyond the past event horizon.
Problem 3: Rindler metric
Consider the set of particles, which move with constant accelerations $a=const>0$ in Minkowski space, with initial conditions at time $t=0$ set as $x=\rho=c^{2}/a$. Let $\tau$ be the proper time of these particles in the units of $\rho/c$. What region of spacetime is parametrized by the pair of positive numbers $(\tau,\rho)$? Express the metric in this region in the coordinates $(\rho,\varphi)$, where $\varphi=c\tau/\rho$. This is the Rindler metric.
Using the expression for $\beta(t)$, we obtain the proper time of the uniformly accelerated observer: \[d\tau=\gamma^{-1}dt= \frac{\mu dt}{\sqrt{\mu^{2}+(eEct)^{2}}},\; \Rightarrow\;\ldots\;\Rightarrow\; c(t-t_{0})=\rho\sinh\frac{\tau}{\rho/c}.\] On substituting $t(\tau)$ into the particle's worldline equation, we express it in parametric form \[\left\{\begin{array}{l} x-x_{0}+\rho=\rho\cosh\frac{c\tau}{\rho},\\ c(t-t_{0})=\rho\sinh\frac{c\tau}{\rho}, \end{array}\right.\] Then we can imagine a collection of particles, accelerating with acceleration $a=const$ with initial conditions $x\big|_{t=t_{0}=0}=x_{0}=\rho$. Their worldlines fill the sector $x>|t-t_{0}|$, and thus its points can be parametrized by two numbers $\rho$ and $\tau$: \[\left(\begin{array}{c}ct\\x\end{array}\right)= \rho \left(\begin{array}{c}\sinh\varphi,\\ \cosh\varphi\end{array}\right), \quad\mbox{where}\quad \varphi=\frac{c\tau}{\rho}\] -- is the hyperbolic angle. In terms of the new coordinate frame $(\varphi,\rho)$ the Minkowskii metric takes the form \begin{equation}\label{Rindler} ds^{2}=\rho^{2}d\varphi^{2}-d\rho^{2}, \quad \rho=\frac{c^{2}}{a}.\end{equation} These coordinates are comoving for the uniformly accelerated observers, by construction. Le us note that Rindler coordinates only work in one of the for sectors $(x+\rho-x_0)>|t-t_0|$ of the Minkowskii space. In order to extend the metric to the whole space, one needs to construct an analytic continuation. In more detail we will consider horizons, maximal extension and other adjoining questions when we look at the spacetime structure of the Schwarzschild black hole.
For more details see textbooks, e.g.
Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald, Gravitation, San Francisco: W. H. Freeman, 1973, ISBN 978-0-7167-0344-0;
G. `t Hooft, Introduction to General Relativity, Caputcollege 1998, ISBN 978-1589490000;
Padmanabhan T. Gravitation: Foundations and Frontiers. CUP, 2010, ISBN 9780521882231.
Metric in curved spacetime
We see here, how, given an arbitrary metric tensor, to determine physical distance between points, local time and physical velocity of a particle in an arbitrary frame of reference.
This problem, though fundamentally important, is necessary in full form only for consideration of particle dynamics in the Kerr metric. In order to analyze the dynamics in the Schwarzschild metric, it suffices to answer all the questions with a substantially simplifying condition $g_{0\alpha}=0$, where $\alpha=1,2,3$ (see the last of the problems).
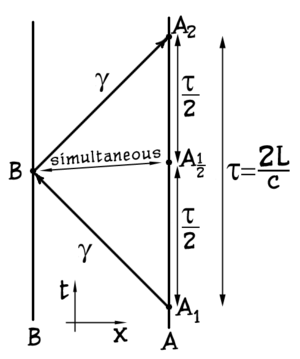
Let the spacetime metric have the general form \[ds^2=g_{\mu\nu}dx^{\mu}dx^{\nu}.\] Coordinates are arbitrary and do not carry direct metrical meaning. An observer, stationary in a given coordinate frame, has 4-velocity $u^{\mu}=(u^{0},0,0,0)$, and the interval determines his proper "local" time \[c^2 d\tau^{2}=ds^{2}=g_{00}(dx^{0})^2.\] An observer in point A, with coordinates $x^\mu$, determines the physical "radar" distance to an infinitely close point $B$, with coordinates $x^{\mu}+dx^{\mu}$, in the following way. She sends a light beam to $B$ and measures the time it takes for the reflected beam to come back. Then distance to $B$ is half the proper time she waited from emission to detection times $c$. It is also natural for her to consider the event of the beam reflection in $B$ to be simultaneous with the middle of the infinitely small 4-distance between the events of emission and detection of light beam in $A$.
Problem 4: measuring distances
Find the proper (physical) distance $dl$ between two events with coordinates $x^\mu$ and $x^\mu+dx^{\mu}$.
First of all, let us agree that the first letters of the Greek alphabet are used to denote the spacelike components: $\alpha,\beta,\gamma=1,2,3$. We can consider spatial points $A$ and $B$ with coordinates $x^{\alpha}$ and $x^{\alpha}+dx^{\alpha}$, and also different events (spacetime points) $A_{i}$ and $B_{i}$ which happen in these points at different times. For light the interval is \[0=ds^2=g_{\mu\nu}dx^\mu dx^\nu = g_{00}(dx^{0})^2+ 2g_{00}g_{0\alpha}dx^{0}dx^{\alpha} +g_{\alpha\beta}dx^{\alpha}dx^{\beta}\] This is a quadratic equation for $dx^0$: \[(dx^{0})_{1,2}=\frac{1}{g_{00}} \big[-g_{0\alpha}dx^\alpha\pm \sqrt{(g_{0\alpha}dx^\alpha)^{2}- g_{00}g_{\alpha\beta}dx^{\alpha}dx^{\beta}} \;\big].\] The two roots correspond to emission and detection of the signal in $B$. The difference is its coordinate time of waiting: \[\widetilde{dx}^0=\frac{(dx^0)_{2}-(dx^0)_{1}}{2}= \frac{2}{g_{00}} \sqrt{(g_{0\alpha}dx^\alpha)^{2}- g_{00}g_{\alpha\beta}dx^{\alpha}dx^{\beta}}.\] The proper time \[d\tau=\frac{1}{c}\sqrt{g_{00}}\;\widetilde{dx}^0\] gives us the physical distance: \[dl=\frac{c\,d\tau}{2}= \frac{\sqrt{g_{00}}}{2}\frac{2}{g_{00}} \sqrt{(g_{0\alpha}dx^\alpha)^{2}- g_{00}g_{\alpha\beta}dx^{\alpha}dx^{\beta}}= \sqrt{\Big(-g_{\alpha\beta} +\frac{g_{0\alpha}g_{0\beta}}{g_{00}}\Big) dx^{\alpha}dx^{\beta}},\] so for the squared distance we obtain \begin{equation}\label{SpaceMetric} dl^{2}=\gamma_{\alpha\beta}dx^{\alpha}dx^{\beta}, \quad\text{where}\quad \gamma_{\alpha\beta}= -g_{\alpha\beta} + \frac{g_{0\alpha}g_{0\beta}}{g_{00}} \end{equation} is the spatial metric.
Problem 5: simultaneous events
Find the difference between coordinate times of two infinitely close simultaneous events.
The coordinate time of the event in $B$ which is considered simultaneous with the event of light reflection in $A$, with coordinates $x^\mu$, is \[x^{0}+\frac{(dx^0)_{2}+(dx^0)_{1}}{2}= x^0-\frac{g_{0\alpha}}{g_{00}}dx^{\alpha}.\] Thus the difference in coordinate times of simultaneous events in points $x^\alpha$ and $x^\alpha+dx^\alpha$ is \begin{equation}\label{Sinchronicity} \delta x^0=-\frac{g_{0\alpha}}{g_{00}}dx^\alpha. \end{equation} It is sometimes convenient to introduce notation \begin{equation}\label{G0alpha} h=g_{00};\quad g_{\alpha}=-\frac{g_{0\alpha}}{g_{00}}.\end{equation} In these terms \[ \gamma_{\alpha\beta}=-g_{\alpha\beta} +h g_{\alpha}g_{\beta};\qquad \delta x^{0}=g_{\alpha}dx^\alpha.\]
Problem 6: observing motion
Let a particle's world line be $x^{\mu}(\lambda)$. What is the proper time interval $\delta\tau$ of a stationary observer, in which this particle covers distance from $x^{\mu}$ to $x^\mu+dx^\mu$?
It is natural to presume that the coordinate time of flight of a particle between points $A$ and $B$, with coordinates $x^\alpha$ and $x^\alpha+dx^\alpha$, is the coordinate time of crossing the point $B$, i.e. $x^0+dx^0$,minus the coordinate time of the event in $B$ which is simultaneous with the event of crossing of point $A$: \[dx^0-\delta x^{0}=dx^0-g_{\alpha}dx^\alpha.\] The corresponding proper time of a local observer is \[c\delta\tau=\sqrt{g_{00}}(dx^{0}-\delta x^{0})= \sqrt{g_{00}}(dx^{0}-g_{\alpha}dx^{\alpha}).\]
Problem 7: proper velocity and Lorentz factor
Proper (or physical) velocity $v$ of the particle is defined as $dl/\delta\tau$. Express it through the $4$-velocity of the particle and through its coordinate velocity $dx^{\alpha}/dx^{0}$; find the interval along the world line $ds$ in terms of $v$ and local time $\delta\tau$.
The proper velocity of a particle is obtained by joining the results of previous two problems \[dl=\sqrt{\gamma_{\alpha\beta}dx^\alpha dx^\beta}; \quad \delta\tau=\frac{1}{c}\sqrt{g_{00}}\cdot (dx^0-g_{\alpha}dx^\alpha).\] Thus, for velocity squared we have \begin{align*}\frac{v^2}{c^2}= &\frac{dl^{2}}{\delta\tau^{2}}= \frac{dl^{2}} {g_{00}\big(dx^0- g_{\alpha}dx^\alpha \big)^{2}}= \frac{\gamma_{\alpha\beta}dx^{\alpha}dx^{\beta}} {g_{00}\big(dx^0- g_{\alpha}dx^\alpha \big)^{2}}= \frac{\gamma_{\alpha\beta}u^{\alpha}u^{\beta}} {g_{00}\big(u^0- g_{\alpha}u^\alpha \big)^{2}}=\\ &=\frac{\gamma_{\alpha\beta} (u^{\alpha}/u^{0})(u^{\beta}/u^{0})} {g_{00}\big(1- g_{\alpha}u^\alpha /u^0\big)^{2}}= \frac{\gamma_{\alpha\beta} \dot{x}^{\alpha}\dot{x}^{\beta}} {g_{00}\big(1- g_{\alpha}\dot{x}^\alpha\big)^{2}}, \end{align*} where $\dot{x}^{\alpha}\equiv \frac{dx^{\alpha}}{dx^{0}}= \frac{dx^{\alpha}/d\lambda}{dx^{0}/d\lambda}= u^\alpha /u^0$. The interval along the worldline of the the particle is then rewritten as \begin{align*} ds^2=&g_{00}(dx^0)^2+2g_{0\alpha}dx^0 dx^\alpha +g_{\alpha\beta}dx^\alpha dx^\beta=\\ =& g_{00} \big(dx^0+g_{0\alpha}dx^\alpha /g_{00}\big)^2 -\frac{g_{0\alpha}g_{0\beta}}{g_{00}} dx^\alpha dx^\beta + g_{\alpha\beta}dx^\alpha dx^\beta=\\ =&g_{00} \big(dx^0-g_{\alpha}dx^\alpha \big)^2 -dl^2=\\ =&g_{00} \big(dx^0-g_{\alpha}dx^\alpha \big)^2 \Big(1-\frac{v^2}{c^2}\Big) =c^{2}\delta\tau^{2} \Big(1-\frac{v^2}{c^2}\Big), \end{align*} and the Lorentz factor appears to be simply related to the $4$-velocity \begin{align}\label{LorentzFactor1} \gamma^{2}=&\Big(1-\frac{v^2}{c^2}\Big)^{-1}= \frac{g_{00} \big(dx^0-g_{\alpha}dx^\alpha \big)^2} {ds^2}= g_{00}(u^{0}-g_{\alpha}u^{\alpha})^{2}=\\ \label{LorentzFactor2} &=\frac{(g_{0\mu}u^\mu)^{2}}{g_{00}}= \frac{(g_{00}u^{0}+g_{0\alpha}u^{\alpha})^2}{g_{00}}= \frac{(u_0)^2}{g_{00}};\\ \label{u0} &\qquad\Rightarrow\qquad u_{0}=\gamma\sqrt{g_{00}}. \end{align}
Problem 8: simplification: static case
How are all the previous answers simplified if $g_{0\alpha}=0$?
If $g_{0\alpha}=0$ we have $g_{\alpha}=0$ and \begin{align} &\gamma_{\alpha\beta}=-g_{\alpha\beta};\quad \delta x^{0}=0;\quad \delta\tau=\sqrt{g_{00}}dx^0;\nonumber\\ \label{IntervalStaticCase} &\frac{v^2}{c^2}= \frac{dl^2}{g_{00}(dx^{0})^{2}}= -\frac{g_{\alpha\beta}}{g_{00}} \dot{x}^\alpha \dot{x}^\beta;\quad ds^2=g_{00}(dx^{0})^{2} \Big(1-\frac{v^2}{c^2}\Big). \end{align}
A coherent exposition can be found in e.g.
L.D. Landau, E.M. Lifshitz (1975). The Classical Theory of Fields. Vol. 2 (4th ed.). Butterworth-Heinemann. ISBN 978-0-7506-2768-9