Difference between revisions of "Characteristic Parameters and Scales"
(Created page with "1") |
(→Problem 10) |
||
| (3 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
[[Category:Standard Cosmological Model|1]] | [[Category:Standard Cosmological Model|1]] | ||
| + | |||
| + | __NOTOC__ | ||
| + | |||
| + | |||
| + | <div id="SCM1"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
| + | Calculate the dark energy density and the cosmological constant value. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">For quark one obtains the following: | ||
| + | SCM assumes $\Omega _\Lambda = 0.73,$ and the Hubble constant value is generally accepted to be $H_0 = 70\, km\cdot s^{-1}\cdot Mpc^{- 1} = 2.26 \cdot 10^{ - 18}s^{-1}.$ Then the critical density corresponds to the following value | ||
| + | \[ | ||
| + | \rho_{cr} = \frac{3H_0^2}{8\pi G} = 0.92 \cdot 10^{-29} g/cm^3 | ||
| + | \] | ||
| + | and | ||
| + | \[\rho _\Lambda = \Omega _\Lambda \rho_{cr} = 0.67 \cdot 10^{-29} g/cm^3.\]</p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="SCM2"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 2 === | ||
| + | Estimate total number of baryons in the Universe. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;"> | ||
| + | $$ | ||
| + | N = \frac{M}{m_n}=\frac{\frac{4}{3}\pi \left( \frac{c}{H_0} \right)^3\rho }{m_n}=\frac{\frac{4}{3}\pi \alpha \left( \frac{c}{H_0}\right)^3\frac{3H_0^2}{8\pi G}}{m_n}= \frac{1}{2}\alpha \frac{H_0^2}{Gm_n}\left( \frac{c}{H_0} \right)^3=\frac{1}{2}\alpha \frac{M_{Pl}}{m_n}\frac{M_{Pl}c^2}{\hbar H_0}\simeq 10^{80}\quad (\alpha \simeq 0.04) | ||
| + | $$ | ||
| + | </p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="SCM_2"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | |||
| + | === Problem 3 === | ||
| + | Find dependence of relative density of dark energy $\Omega_\Lambda$ on the redshift. Plot $\Omega_\Lambda(z)$. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;"> | ||
| + | Neglecting the contribution of radiation ($\rho _{r0} \ll \rho _{m0} < \rho _\Lambda$) one obtains | ||
| + | $$ | ||
| + | \Omega _\Lambda (z) = \frac{\rho _\Lambda }{\rho _{cr}(z)} = \frac{\rho _\Lambda}{\rho _{m0}(1 + z)^3 + \rho _\Lambda } = \frac{\Omega _{\Lambda 0}} | ||
| + | {\Omega _{m0}(1 + z)^3 + \Omega _{\Lambda 0}}; | ||
| + | $$ | ||
| + | $$ | ||
| + | \Omega _\Lambda (z) \simeq \frac{1}{\frac{1}{3}(1 + z)^3+ 1} | ||
| + | $$ | ||
| + | <gallery widths=600px heights=500px> | ||
| + | File:12_1.jpg| | ||
| + | </gallery> | ||
| + | </p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | <div id="SCM3"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 4 === | ||
| + | Estimate total number of stars in the Universe. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;"> | ||
| + | $$ | ||
| + | \begin{gathered} | ||
| + | \rho_{cr} \equiv \frac{3H_0^2}{8\pi G} \simeq 10^{-29}\mbox{g/cm}^3; \\ | ||
| + | \rho_{bar}\simeq 0.04\rho _{cr}; \\ | ||
| + | R_H \approx 10^{28}\mbox{cm}; \\ | ||
| + | M_{bar} \approx 0.2 \times 10^{55}\,cm; \\ | ||
| + | M_ \odot\simeq 10^{33}\,cm; \\ | ||
| + | N_ \odot \approx 10^{21}. \\ | ||
| + | \end{gathered} | ||
| + | $$ | ||
| + | </p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | <div id="SCM4"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 5 === | ||
| + | Find the ratio of dark energy density to the energy density of electric field of intensity $1\,V/m$. Compare the dark energy density with gravitational field energy density on the Earth surface. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;"> | ||
| + | Transit from the relative density $\Omega_{DE}$ to th usual one $\rho_{DE}=\Omega_{DE}\rho_{cr}.$ The present value of the critical density of Universe is | ||
| + | $$\rho_{cr}\simeq 9\times 10^{-10} \;\mbox{J/m}^3,$$ | ||
| + | therefore | ||
| + | $$ | ||
| + | \rho_{DE}\simeq 6.3\times 10^{-10} \;J/m^3 | ||
| + | $$ | ||
| + | which is equivalent to the mass density | ||
| + | $$ | ||
| + | \rho _{DE}^{(m)}\simeq 0.7\times 10^{-26}\;kg/m^3\simeq 3.9\;GeV/s^2\,m^3\simeq 4 \;proton mass/m^3 | ||
| + | $$ | ||
| + | |||
| + | Compare $\rho_{DE}$ with the energy density of the electric field $\rho_{E}$ with intensity $E=1\;V/m$ (such electric fields are easily available for laboratory measurements). For this field one gets | ||
| + | $$ | ||
| + | \rho_E = \frac{\varepsilon_0E^2}{2} = 4.4 \times 10^{- 12}\mbox{J/m}^3. | ||
| + | $$ | ||
| + | |||
| + | As one can see, it is possible to measure fields with energy density which is orders of magnitude less than the dark energy density. However the measurement of dark energy is far from being trivial. Unlike the the electric field, the dark energy cannot be switched on and off. The dark energy, at least in the form of cosmological constant, is homogeneously distributed in space, and we presently have no means to create local regions of increased dark energy density, similar to a capacitor in the case of the electric field. At last let us compare the dark energy density under interest to that of gravity field on the Earth surface where the laboratory measurements are performed. The latter equals to | ||
| + | $$ | ||
| + | \rho _G = \frac{g^2}{8\pi G} = 5.7 \times 10^{+10} \mbox{J/m}^3. | ||
| + | $$ | ||
| + | It is clear that if the background exceeds the measured quantity in twenty orders of magnitude, then reliable identification of this quantity requires a super-precision experiment. | ||
| + | </p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | <div id="SCM5"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 6 === | ||
| + | Estimate the distance between two neutral hydrogen atoms at which the gravitational force of their attraction is balanced by the repulsion force generated by dark energy in the form of cosmological constant. Make the same estimates for the | ||
| + | Sun-Earth system. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;"> | ||
| + | $$ | ||
| + | \ddot R = \frac{\ddot a}{a}R. | ||
| + | $$ | ||
| + | The acceleration generated by the cosmological constant is | ||
| + | $$\begin{gathered} | ||
| + | \ddot R = \frac{\ddot a}{a}R = - \frac{4\pi G}{3}(\rho _\Lambda + 3p_\Lambda )R = \frac{8\pi G}{3}\rho _\Lambda R; \\ | ||
| + | \frac{\rho _{\Lambda 0}}{\rho _{cr0}} = \Omega _{\Lambda 0};\quad \rho _{cr0} = \frac{3H_0^2}{8\pi G} \\ | ||
| + | \end{gathered} | ||
| + | $$ | ||
| + | Then the contribution of the cosmological constant into the current acceleration is $\ddot R = \Omega _{\Lambda 0}H_0^2R.$ This quantity is to be compared with the usual gravity acceleration generated by the mass $M,$ | ||
| + | $$ | ||
| + | g = G\frac{M}{R^2} | ||
| + | $$ | ||
| + | Then for the case of hydrogen atom one obtains | ||
| + | \[R = \left(\frac{Gm_p}{H_0^2\Omega _{\Lambda 0}} \right)^{1/3}\simeq 0.3 \, m.\] | ||
| + | |||
| + | For the Sun-Earth system the analogues estimate gives | ||
| + | $$ | ||
| + | R=\frac{2\pi R_{a.u.}}{H_0\sqrt{\Omega_{\Lambda 0}}}\simeq 0.5 \,Mpc, | ||
| + | $$ | ||
| + | where $R_{a.u.}-$ is the mean Sun-Earth distance. | ||
| + | </p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="SCM6"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 7 === | ||
| + | Calculate magnitude of physical acceleration. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;"> | ||
| + | $$ | ||
| + | \begin{gathered} | ||
| + | \dot V = (\dot H + H^2)R; \\ | ||
| + | H \equiv \frac{\dot a}{a};\;\dot H = \frac{\ddot aa - \dot a^2}{a^2} =\frac{\ddot a}{a} - H^2; \\ | ||
| + | \dot H + H^2 = - \frac{4\pi G}{3}(\rho + 3p) = - \frac{4\pi G}{3}( - 2\rho _\Lambda + \rho _m) = \\ | ||
| + | = \frac{8\pi G}{3}\left( \rho _\Lambda - \frac{1}{2}\rho _m \right) = H_0^2\left( \Omega _{\Lambda 0} - \frac{1}{2}\Omega _{m 0} \right); \\ | ||
| + | \dot V = H_0^2R\left( \Omega _{\Lambda 0 } - \frac{1}{2}\Omega _{m 0} \right) \\ | ||
| + | \end{gathered} | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \begin{gathered} | ||
| + | R = 1\, Mpc;\\ | ||
| + | \dot V \simeq 10^{ - 11}\, sm/s^2 \\ | ||
| + | \end{gathered} | ||
| + | $$ | ||
| + | |||
| + | </p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <div id="SCM7"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 8 === | ||
| + | How far can one see in the Universe? | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;"> | ||
| + | The particle horizon limits the causally connected region of the Universe, which is in principle observable at given time moment. by definition it is | ||
| + | $$ | ||
| + | L_{p} = a\int\limits_{0}^t\frac{dt}{a\left( t \right)}. | ||
| + | $$ | ||
| + | where | ||
| + | $a(t) = A^{1/3}\sinh ^{2/3}\left( t/{t_\Lambda }\right)$ | ||
| + | and | ||
| + | $t_\Lambda \equiv \frac{2}{3}\left(H_0 \right)^{-1}\left( \Omega _{\Lambda 0}\right)^{ - 1/2}\simeq 10.768 \cdot 10^{9}$ years. | ||
| + | $t_0 = t_\Lambda Arth\sqrt {\Omega _{\Lambda 0}}\simeq 13.7\cdot10^9 $ years. | ||
| + | \[A \equiv \frac{\Omega_{m0}}{\Omega _{\Lambda 0}} = | ||
| + | \frac{1 - \Omega _{\Lambda 0}}{\Omega _{\Lambda 0}} = 0.37.\] | ||
| + | After integration one finally obtains | ||
| + | $L_{p} = 47.563\cdot 10^9$ light years. | ||
| + | </p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | <div id="SCM8"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 9 === | ||
| + | Find age of the Universe. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;"> | ||
| + | Using the result of the previous problem, one obtains the age of the Universe from the condition $a(t_0) = a_0 = 1$ | ||
| + | $$ | ||
| + | t_0 = \frac{2}{3}\left( H_0\right)^{-1}\left(\Omega _{\Lambda 0}\right)^{-1/2}Arsh \sqrt{\frac{\Omega _{\Lambda 0}}{\Omega _{m0}}} | ||
| + | $$ | ||
| + | or | ||
| + | $$ | ||
| + | t_0 = t_\Lambda Arsh\sqrt {\frac{\Omega _{\Lambda 0}}{\Omega _{m0}}} | ||
| + | $$ | ||
| + | Using the relation $Arth(x) = Arsh\left(x/\sqrt {1 - x^2}\right)$ one gets | ||
| + | \[ | ||
| + | t_0 = t_\Lambda Arth\sqrt {\Omega _{\Lambda 0}} | ||
| + | \simeq 13.7\cdot 10^9 years.\] | ||
| + | </p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <div id="SCM9"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 10 === | ||
| + | Give a qualitative explanation why the age of the Universe in SCM is considerably larger than the age of matter dominated Universe (the Einstein-de Sitter model). | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;"> | ||
| + | In the Einstein-de Sitter model the expansion is always decelerating, while in the SCM the decelerated expansion turns to the accelerated one. Therefore for a given Hubble constant $H_0$ the preceding value in the Einstein-de Sitter model was greater than that in the SCM, and the average expansion rate was also greater, so the observed size of the Universe was reached in a smaller period of time. | ||
| + | </p> | ||
| + | </div> | ||
| + | </div></div> | ||
Latest revision as of 17:29, 13 October 2012
Problem 1
Calculate the dark energy density and the cosmological constant value.
For quark one obtains the following: SCM assumes $\Omega _\Lambda = 0.73,$ and the Hubble constant value is generally accepted to be $H_0 = 70\, km\cdot s^{-1}\cdot Mpc^{- 1} = 2.26 \cdot 10^{ - 18}s^{-1}.$ Then the critical density corresponds to the following value \[ \rho_{cr} = \frac{3H_0^2}{8\pi G} = 0.92 \cdot 10^{-29} g/cm^3 \] and \[\rho _\Lambda = \Omega _\Lambda \rho_{cr} = 0.67 \cdot 10^{-29} g/cm^3.\]
Problem 2
Estimate total number of baryons in the Universe.
$$ N = \frac{M}{m_n}=\frac{\frac{4}{3}\pi \left( \frac{c}{H_0} \right)^3\rho }{m_n}=\frac{\frac{4}{3}\pi \alpha \left( \frac{c}{H_0}\right)^3\frac{3H_0^2}{8\pi G}}{m_n}= \frac{1}{2}\alpha \frac{H_0^2}{Gm_n}\left( \frac{c}{H_0} \right)^3=\frac{1}{2}\alpha \frac{M_{Pl}}{m_n}\frac{M_{Pl}c^2}{\hbar H_0}\simeq 10^{80}\quad (\alpha \simeq 0.04) $$
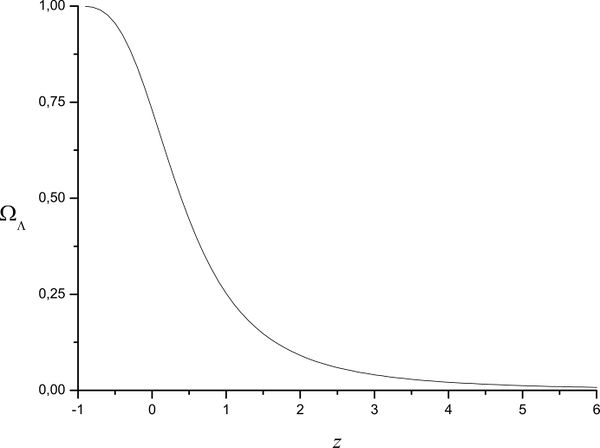
Problem 3
Find dependence of relative density of dark energy $\Omega_\Lambda$ on the redshift. Plot $\Omega_\Lambda(z)$.
Neglecting the contribution of radiation ($\rho _{r0} \ll \rho _{m0} < \rho _\Lambda$) one obtains $$ \Omega _\Lambda (z) = \frac{\rho _\Lambda }{\rho _{cr}(z)} = \frac{\rho _\Lambda}{\rho _{m0}(1 + z)^3 + \rho _\Lambda } = \frac{\Omega _{\Lambda 0}} {\Omega _{m0}(1 + z)^3 + \Omega _{\Lambda 0}}; $$ $$ \Omega _\Lambda (z) \simeq \frac{1}{\frac{1}{3}(1 + z)^3+ 1} $$
Problem 4
Estimate total number of stars in the Universe.
$$ \begin{gathered} \rho_{cr} \equiv \frac{3H_0^2}{8\pi G} \simeq 10^{-29}\mbox{g/cm}^3; \\ \rho_{bar}\simeq 0.04\rho _{cr}; \\ R_H \approx 10^{28}\mbox{cm}; \\ M_{bar} \approx 0.2 \times 10^{55}\,cm; \\ M_ \odot\simeq 10^{33}\,cm; \\ N_ \odot \approx 10^{21}. \\ \end{gathered} $$
Problem 5
Find the ratio of dark energy density to the energy density of electric field of intensity $1\,V/m$. Compare the dark energy density with gravitational field energy density on the Earth surface.
Transit from the relative density $\Omega_{DE}$ to th usual one $\rho_{DE}=\Omega_{DE}\rho_{cr}.$ The present value of the critical density of Universe is $$\rho_{cr}\simeq 9\times 10^{-10} \;\mbox{J/m}^3,$$ therefore $$ \rho_{DE}\simeq 6.3\times 10^{-10} \;J/m^3 $$ which is equivalent to the mass density $$ \rho _{DE}^{(m)}\simeq 0.7\times 10^{-26}\;kg/m^3\simeq 3.9\;GeV/s^2\,m^3\simeq 4 \;proton mass/m^3 $$ Compare $\rho_{DE}$ with the energy density of the electric field $\rho_{E}$ with intensity $E=1\;V/m$ (such electric fields are easily available for laboratory measurements). For this field one gets $$ \rho_E = \frac{\varepsilon_0E^2}{2} = 4.4 \times 10^{- 12}\mbox{J/m}^3. $$ As one can see, it is possible to measure fields with energy density which is orders of magnitude less than the dark energy density. However the measurement of dark energy is far from being trivial. Unlike the the electric field, the dark energy cannot be switched on and off. The dark energy, at least in the form of cosmological constant, is homogeneously distributed in space, and we presently have no means to create local regions of increased dark energy density, similar to a capacitor in the case of the electric field. At last let us compare the dark energy density under interest to that of gravity field on the Earth surface where the laboratory measurements are performed. The latter equals to $$ \rho _G = \frac{g^2}{8\pi G} = 5.7 \times 10^{+10} \mbox{J/m}^3. $$ It is clear that if the background exceeds the measured quantity in twenty orders of magnitude, then reliable identification of this quantity requires a super-precision experiment.
Problem 6
Estimate the distance between two neutral hydrogen atoms at which the gravitational force of their attraction is balanced by the repulsion force generated by dark energy in the form of cosmological constant. Make the same estimates for the Sun-Earth system.
$$ \ddot R = \frac{\ddot a}{a}R. $$ The acceleration generated by the cosmological constant is $$\begin{gathered} \ddot R = \frac{\ddot a}{a}R = - \frac{4\pi G}{3}(\rho _\Lambda + 3p_\Lambda )R = \frac{8\pi G}{3}\rho _\Lambda R; \\ \frac{\rho _{\Lambda 0}}{\rho _{cr0}} = \Omega _{\Lambda 0};\quad \rho _{cr0} = \frac{3H_0^2}{8\pi G} \\ \end{gathered} $$ Then the contribution of the cosmological constant into the current acceleration is $\ddot R = \Omega _{\Lambda 0}H_0^2R.$ This quantity is to be compared with the usual gravity acceleration generated by the mass $M,$ $$ g = G\frac{M}{R^2} $$ Then for the case of hydrogen atom one obtains \[R = \left(\frac{Gm_p}{H_0^2\Omega _{\Lambda 0}} \right)^{1/3}\simeq 0.3 \, m.\] For the Sun-Earth system the analogues estimate gives $$ R=\frac{2\pi R_{a.u.}}{H_0\sqrt{\Omega_{\Lambda 0}}}\simeq 0.5 \,Mpc, $$ where $R_{a.u.}-$ is the mean Sun-Earth distance.
Problem 7
Calculate magnitude of physical acceleration.
$$ \begin{gathered} \dot V = (\dot H + H^2)R; \\ H \equiv \frac{\dot a}{a};\;\dot H = \frac{\ddot aa - \dot a^2}{a^2} =\frac{\ddot a}{a} - H^2; \\ \dot H + H^2 = - \frac{4\pi G}{3}(\rho + 3p) = - \frac{4\pi G}{3}( - 2\rho _\Lambda + \rho _m) = \\ = \frac{8\pi G}{3}\left( \rho _\Lambda - \frac{1}{2}\rho _m \right) = H_0^2\left( \Omega _{\Lambda 0} - \frac{1}{2}\Omega _{m 0} \right); \\ \dot V = H_0^2R\left( \Omega _{\Lambda 0 } - \frac{1}{2}\Omega _{m 0} \right) \\ \end{gathered} $$ $$ \begin{gathered} R = 1\, Mpc;\\ \dot V \simeq 10^{ - 11}\, sm/s^2 \\ \end{gathered} $$
Problem 8
How far can one see in the Universe?
The particle horizon limits the causally connected region of the Universe, which is in principle observable at given time moment. by definition it is $$ L_{p} = a\int\limits_{0}^t\frac{dt}{a\left( t \right)}. $$ where $a(t) = A^{1/3}\sinh ^{2/3}\left( t/{t_\Lambda }\right)$ and $t_\Lambda \equiv \frac{2}{3}\left(H_0 \right)^{-1}\left( \Omega _{\Lambda 0}\right)^{ - 1/2}\simeq 10.768 \cdot 10^{9}$ years. $t_0 = t_\Lambda Arth\sqrt {\Omega _{\Lambda 0}}\simeq 13.7\cdot10^9 $ years. \[A \equiv \frac{\Omega_{m0}}{\Omega _{\Lambda 0}} = \frac{1 - \Omega _{\Lambda 0}}{\Omega _{\Lambda 0}} = 0.37.\] After integration one finally obtains $L_{p} = 47.563\cdot 10^9$ light years.
Problem 9
Find age of the Universe.
Using the result of the previous problem, one obtains the age of the Universe from the condition $a(t_0) = a_0 = 1$ $$ t_0 = \frac{2}{3}\left( H_0\right)^{-1}\left(\Omega _{\Lambda 0}\right)^{-1/2}Arsh \sqrt{\frac{\Omega _{\Lambda 0}}{\Omega _{m0}}} $$ or $$ t_0 = t_\Lambda Arsh\sqrt {\frac{\Omega _{\Lambda 0}}{\Omega _{m0}}} $$ Using the relation $Arth(x) = Arsh\left(x/\sqrt {1 - x^2}\right)$ one gets \[ t_0 = t_\Lambda Arth\sqrt {\Omega _{\Lambda 0}} \simeq 13.7\cdot 10^9 years.\]
Problem 10
Give a qualitative explanation why the age of the Universe in SCM is considerably larger than the age of matter dominated Universe (the Einstein-de Sitter model).
In the Einstein-de Sitter model the expansion is always decelerating, while in the SCM the decelerated expansion turns to the accelerated one. Therefore for a given Hubble constant $H_0$ the preceding value in the Einstein-de Sitter model was greater than that in the SCM, and the average expansion rate was also greater, so the observed size of the Universe was reached in a smaller period of time.