Difference between revisions of "Information, Entropy and Holographic Screen"
(→Problem 6:) |
|||
| Line 98: | Line 98: | ||
| − | <div id=""></div> | + | <div id="HU07"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| − | |||
=== Problem 1: === | === Problem 1: === | ||
| − | + | According to Hawking, black holes emit photons (the black hole evaporation) with thermal spectrum and effective temperature | |
| + | $$ | ||
| + | T_{BH}=\frac{\hbar c}{4\pi k_{_B}}r_{g}, | ||
| + | $$ | ||
| + | where $r_{g}={2GM}/{c^2}$ is the black hole Schwarzschild radius. Neglecting accretion and CMB absorption, determine the life time of a black hole with initial mass $M_{0}.$ Calculate the lifetime for black holes with the mass equal to Planck mass, mass of the Earth and Solar mass. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">The black hole mass changes due to evaporation according to |
| + | $$ | ||
| + | \frac{dM}{dt}=-\frac{\sigma T_{H}^4A_{BH}}{c^2}, | ||
| + | $$ | ||
| + | where \[\sigma =\frac{\pi^2k_{_B}^4}{60\hbar^3c^2}\] is the Stefan-Boltzmann constant, and $A_{BH}=4\pi r_g^2$ is the surface area of the black hole. Therefore | ||
| + | $$M(t)=\frac{M_{0}}{(1-t/\tau )^{1/3}},$$ where the lifetime of the black hole equals to | ||
| + | $$\tau =\frac{5120\pi G^2M_{0}^3}{\hbar c^4}.$$ | ||
| + | Characteristic lifetimes are the following: | ||
| + | \[{{\left. \tau \right|}_{{{M}_{0}}={{M}_{Pl}}}}=5120\pi {{t}_{Pl}}\sim {{10}^{-39}}s,\] \[{{\left. \tau \right|}_{{{M}_{0}}={{M}_{\oplus }}}}\sim {{10}^{58}}c\sim {{10}^{50}}\;\mbox{\it years,}\] \[{{\left. \tau \right|}_{{{M}_{0}}={{M}_{\odot }}}}\sim {{10}^{75}}c\sim {{10}^{67}}\;\mbox{\it years.}\]</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 112: | Line 123: | ||
| − | <div id=""></div> | + | <div id="HU08"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Show that black holes have negative thermal capacity. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">The black hole entropy has the form \[S_{BH}=\frac{M_{Pl}^2}{16\pi k_B T^2},\] its temperature equals to \[T_{BH}=\frac{M_{Pl}^2}{8\pi k_BM},\] then its thermal capacity is |
| + | \begin{equation} | ||
| + | \label{C_{BH}} | ||
| + | C_{BH}=T\left( \frac{\partial S}{\partial T}\right)=-8\pi k_B\frac{M^2}{M_{Pl}^2}. | ||
| + | \end{equation}</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 125: | Line 140: | ||
| − | <div id=""></div> | + | <div id="HU09"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Show that the black hole evaporation process is accompanied by increase of its temperature. Find the relative variation of the black hole temperature if its mass gets twice smaller due to evaporation. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">When the black hole mass is halved, its temperature becomes twice as high.</p> |
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 138: | Line 153: | ||
| − | <div id=""></div> | + | <div id="HU10"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Show that in order to produce an entropy force when a particle approaches the holographic screen, its temperature must be finite. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Temperature is defined as |
| + | $$ | ||
| + | \frac{dS}{dE}=\frac{1}{T}. | ||
| + | $$ | ||
| + | Any motion of a particle (or propagation of excitation) leads to entropy change $\Delta S\sim \Delta x$ and therefore to change of energy. Thus the screen temperature must be finite by definition. In other words, the relation $\Delta E=T\Delta S$ can hold only at finite temperatures.</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 151: | Line 170: | ||
| − | <div id=""></div> | + | <div id="HU11"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Determine the entropic acceleration of a particle crossing the holographic screen with temperature ${{T}_{b}}$. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">$$ |
| + | a_e=\frac{F_e}{m}=T_b\frac{\Delta S}{\Delta x}=2\pi T_b\frac{k_{_B}c}{\hbar}. | ||
| + | $$</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 164: | Line 185: | ||
| − | <div id=""></div> | + | <div id="HU12"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Show that the Unruh temperature is the Hawking radiation temperature $$T_{BH}=\frac{\hbar c^3}{8\pi k_{_B}GM}$$ with substitution $a\to g,$ where $g$ is the surface gravity of the black hole. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Substitute the relation $GM=gr_{g}^2$ into the formula for the hawking radiation temperature and take into account the definition of gravity radius $r_{g}=\frac{2MG}{c^2}$=$\frac{c^2}{2g},$ to obtain |
| + | $$ | ||
| + | T_{BH}=\frac{\hbar g}{2\pi k_{_B}c}=T_{_U}(a=g). | ||
| + | $$</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 177: | Line 201: | ||
| − | <div id=""></div> | + | <div id="HU13"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | In order to verify experimentally the Unruh effect, it is planned to accelerate particles with acceleration of the order of $10^{26} \mbox{\it m/}\sec^2$. What vacuum temperature does this acceleration correspond to? | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">$$ |
| + | T_{_U}(a={10^{26}} \mbox{\it m/s}^{2})\simeq 4\times 10^5 K. | ||
| + | $$</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 190: | Line 216: | ||
| − | <div id=""></div> | + | <div id="HU14"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Derive the second Newton's law from the holographic principle. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Entropic force acting on a test particle of mass $m,$ which approaches the holographic screen with temperature $T$, equals to |
| + | $$ | ||
| + | F=T\frac{\Delta S}{\Delta x}=2\pi {{k}_{_B}}\frac{mc}{\hbar }T. | ||
| + | $$ | ||
| + | Treating the temperature $T$ as the Unruh one (see \ref{Hol_f_Unruh:4}) | ||
| + | $$ | ||
| + | T=\frac{1}{2\pi {{k}_{_B}}}\frac{\hbar }{c}a, | ||
| + | $$ | ||
| + | one obtains the second Newton's law | ||
| + | $$ | ||
| + | F=ma. | ||
| + | $$</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 203: | Line 240: | ||
| − | <div id=""></div> | + | <div id="HU15"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Show that the inertia law can be obtained from the holographic principle. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Consider a particle of mass $m,$ approaching the holographic screen. At some moment the particle must merge with the microscopic degrees of freedom on the screen, and thus it will consist of the same $n$ bits, like those ''living'' on the screen. As every bit transmits energy equal to $\frac{1}{2}{{k}_{B}}T,$ the following must hold |
| + | $$ | ||
| + | mc^2=\frac{1}{2}nk_{_B}T. | ||
| + | $$ | ||
| + | Substitute the mass into the expression for the entropic force and make use the definition of the Unruh temperature (\ref{Hol_f_Unruh:4}) to express the entropy change in terms of the acceleration | ||
| + | $$ | ||
| + | \frac{\Delta S}{n\Delta x}=k_{_B}\frac{a}{2c^2}. | ||
| + | $$ | ||
| + | The obtained equation represents the ''holographic'' version of the inertia law: if entropy gradients are absent, then the entropic forces are zeros and as a consequence the acceleration of the particle equals to zero.</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 216: | Line 261: | ||
| − | <div id=""></div> | + | <div id="HU16"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Obtain the Newton's law of universal gravitation using the holographic principle. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Consider a particle of mass $m$ approaching the holographic screen. The particle feels the entropic force |
| + | $$ | ||
| + | F=T\frac{\Delta S}{\Delta x}=2\pi Tk_{_B}\frac{mc}{\hbar }, | ||
| + | $$ | ||
| + | where $T$ is the holographic screen temperature. Make use of the equipartition theorem | ||
| + | $$ | ||
| + | E=\frac{1}{2}N k_{_B}T. | ||
| + | $$ | ||
| + | Here $N$ is the number of degrees of freedom on the screen, which according to the holographic principle equals to (more precisely, cannot exceed) | ||
| + | $$ | ||
| + | N=\frac{Ac^3}{G\hbar }=\frac{4\pi R^2 c^3}{G\hbar }. | ||
| + | $$ | ||
| + | Treating $E$ as $M{{c}^{2}},$ where $M$ is the mass concentrated in the region which is enclosed by the holographic screen, one obtains the temperature | ||
| + | $$ | ||
| + | T=\frac{Mc^2}{2k_{_B}\pi R^2}\frac{G\hbar }{c^3}. | ||
| + | $$ | ||
| + | Then substitute the obtained temperature into the original expression for the entropic force to recover the Newton's law of universal gravitation | ||
| + | $$ | ||
| + | F=G\frac{mM}{R^2}. | ||
| + | $$</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 229: | Line 293: | ||
| − | <div id=""></div> | + | <div id="HU17"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Compare how close to a black hole are Earth, Sun and observable Universe. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Compare the (Schwarzschild) gravity radii $r_{g}$ and the physical ones $R$ for the Earth and the Sun. For the latter $R\simeq 7\times 10^5 \mbox{\it km},$ and $r_g\simeq 3\mbox{\it km}.$ For the Earth $R\simeq 6400 \mbox{\it km},$ and $r_g\simeq 3\mbox{\it cm}.$ Thus those objects are not similar at all to a black hole. Analogous estimate for the observable part of the Universe enclosed by the Hubble sphere with the radius $R_{H}=c H^{-1}$, gives |
| + | $$ | ||
| + | \begin{gathered} | ||
| + | r_{g,univ}=\frac{2GM_{univ}}{c^2}; \hfill \\ | ||
| + | R_{H}=cH^{-1}; \\ | ||
| + | M_{univ}=\frac{4\pi }{3}R_H^{3}\rho ; \hfill \\ | ||
| + | H^2=\frac{8\pi G}{3}\rho \to \rho =\frac{3H^2}{8\pi G}; \hfill \\ | ||
| + | M_{univ}=\frac{4\pi }{3}R_H^3\frac{3H^2}{8\pi G}=\frac{c^2R_H}{2G}; \\ | ||
| + | R_H=\frac{2GM_{univ}}{c^2}=r_{g,univ}. \hfill \\ | ||
| + | \end{gathered} | ||
| + | $$ | ||
| + | It is this impressive "coincidence" which allows us to use the argumentation of black hole thermodynamics for the holographic description of the Universe.</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 242: | Line 317: | ||
| − | <div id=""></div> | + | <div id="HU18"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Estimate the temperature of the Hubble sphere, considering it as a holographic screen. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">To obtain the required estimate, make use of the "similarity" of the observed Universe to a black hole (see the previous problem). The spectrum of the Hawking radiation for massless fields appeared to coincide with the black body radiation, which allows one to assign to the black hole the temperature |
| + | $$ | ||
| + | T_{BH}=\frac{\hbar c^3}{8\pi Gk_{_B}M} | ||
| + | $$ | ||
| + | Transform this formula using the first Friedman equation | ||
| + | $$ | ||
| + | T_{BH}=\frac{\hbar c^3}{8\pi Gk_{_B}M}=\frac{1}{3}\frac{\hbar c^3}{k_B}\frac{\rho }{MH^2}=\frac{1}{3}\frac{\hbar c^3}{k_{_B}}\frac{1}{VH^2}. | ||
| + | $$ | ||
| + | Substitute \[V=\frac{4\pi }{3}R_{H}^3\] and take into account that the Hubble radius equals to $R_{H}=cH^{-1}$ to obtain the temperature of the Hubble sphere | ||
| + | \begin{equation} | ||
| + | \label{T_{H-univ}} | ||
| + | T_{H}=\frac{\hbar H}{4\pi k_{_B}}\sim 10^{-30}\:K. | ||
| + | \end{equation}</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 255: | Line 342: | ||
| − | <div id=""></div> | + | <div id="HU19"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Show that equilibrium between the relic radiation and holographic screen is possible only at Planck temperature. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Temperature of the radiation-dominated Universe depends on time as |
| + | \begin{equation} | ||
| + | T=\left( \frac{3}{32\pi G\alpha } \right)^{1/4}t^{-1/2}, | ||
| + | \end{equation} | ||
| + | where $\alpha $ is constant ($\rho =\alpha T^4$.) Combine the latter expression with the formula (\ref{T_{H-univ}}) and take into account that $H=\left( 2t \right)^{-1}$ for radiation, to obtain | ||
| + | $$ | ||
| + | T_{H}=\frac{\hbar }{8\pi k_{_B}}\left( \frac{32\pi G\alpha }{2} \right)^{1/2}T_{CMB}^{2}\sim T_{CMB}^{2}\sqrt{G}\simeq \frac{T_{CMB}^{2}}{T_{Pl}} | ||
| + | $$ | ||
| + | where ${{T}_{Pl}}={{\left( \hbar {{c}^{5}}/Gk_{B}^{2} \right)}^{1/2}}=1.4\cdot {{10}^{32}}K$ is the Planck temperature. | ||
| + | |||
| + | Note that the obtained expression is valid for any stage of Universe's evolution, because its temperature is always mostly determined by radiation. Temperature of the matter relaxes to that of radiation, as the thermal capacity of the latter is considerably higher. Therefore according to relation (\ref{T_{H-univ}}) the equilibrium between the relic radiation and the holographic screen is possible only at the Planck temperature.</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 268: | Line 365: | ||
| − | <div id=""></div> | + | <div id="HU20"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | According to the holographic ideology, all physical phenomena can be described by the boundary layer theory. Therefore a conclusion comes that one should account for contribution of such surface terms while deriving the equations of General Relativity. Show that consideration of the boundary terms in the Einstein-Hilbert action is equivalent to introduction of non-zero energy-momentum tensor into the standard Einstein equations. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Action for the gravitational field is |
| + | \begin{equation} | ||
| + | S_{EH} \,=\,- \frac{c^{3}}{16 \pi G} \int d^{4} x \,\sqrt{-g} \,R\, . | ||
| + | \label{2.1} | ||
| + | \end{equation} | ||
| + | Variation of the action with respect to metric $g_{\mu \nu}$ (see problem $25$ of Chapter 2) in a compact region $\Omega$ gives | ||
| + | \begin{eqnarray} | ||
| + | \lefteqn{ | ||
| + | \delta \int_{\Omega} d^{4}x \sqrt{-g}\, R \, =} \nonumber \\ | ||
| + | & & | ||
| + | \int_{\Omega}d^{4} x | ||
| + | \sqrt{-g} | ||
| + | \Biggl[ \left( g^{\mu \nu}\nabla^2 \delta g_{\mu \nu}\,- \nabla^{\mu} \nabla^{\nu} | ||
| + | \delta g_{\mu \nu} \right) | ||
| + | -\left( R^{\mu \nu} - \frac{1}{2}\, g^{\mu \nu} R | ||
| + | \right) \delta g_{\mu \nu} \Biggr] \, , \label{2.2} | ||
| + | \end{eqnarray} | ||
| + | where $\nabla^2 \,=\, g^{\alpha \beta} \nabla_{\alpha} \, \nabla_{\beta}$. | ||
| + | The functional $S_{Boundary}[g],$ thus takes the form | ||
| + | \begin{equation} | ||
| + | \delta S_{Boundary}[g]\,=\,-\, \frac{1}{16 \pi G} \int_{\Omega}d^{4}x \sqrt{-g} | ||
| + | \Bigl( g^{\mu | ||
| + | \nu} \nabla^2 \delta g_{\mu \nu}\,-\, \nabla^{\mu} \nabla^{\nu} \delta | ||
| + | g_{\mu \nu} \Bigr) \, , \label{2.4} | ||
| + | \end{equation} | ||
| + | The Einstein equations including the contribution of boundary terms take the form | ||
| + | \begin{eqnarray} | ||
| + | R^{\mu \nu} - \frac{1}{2}\, g^{\mu \nu} R = 8 \pi G\, T^{\mu \nu}_{Boundary}\, , \nonumber \\ | ||
| + | T^{\mu \nu}_{Boundary} = \frac{2}{\sqrt{- g}} \, \frac{\delta S_{Boundary}} | ||
| + | {\delta g_{\mu \nu}}\,. \label{2.5} | ||
| + | \end{eqnarray} | ||
| + | Note that in the case of flat space-time with $g_{\mu \nu}=const,$ the boundary action $S_{Boundary}[g] = 0,$ and the Einstein equation take the standard form.</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 281: | Line 409: | ||
| − | <div id=""></div> | + | <div id="HU21"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Derive the Friedman equations from the holographic principle. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">'''1st method.''' |
| + | |||
| + | As shown in problem \ref{HU17} of the present Chapter, one can use the argumentation of black hole thermodynamics for the holographic description of the Universe. Let the holographic screen coincide with the Hubble sphere (the sphere of radius $R=H^{-1}$). The screen has area $A=4\pi R^2$ and carries the (maximum) information $N=4\pi R^2/L_{Pl}^{2}\; \mbox{bit.}$ Change of information $dN$ during time $dt$, which corresponds to expansion of the Universe from $R$ to $R+dR$, equals to | ||
| + | $$ | ||
| + | dN=\frac{dA}{L_{Pl}^2}=\frac{8\pi R}{L_{Pl}^2}dR. | ||
| + | $$ | ||
| + | Here $c=k_{_B}=1.$ Increase of the Hubble radius leads to the change of the Hawking temperature | ||
| + | ($T=\hbar/(2\pi R)$) by | ||
| + | $$ | ||
| + | dT=-\frac{\hbar }{2\pi R^2}dR. | ||
| + | $$ | ||
| + | From the equipartition theorem | ||
| + | \begin{equation} | ||
| + | \label{HolPr:15_1} | ||
| + | dE=\frac{1}{2}NdT+\frac{1}{2}TdN=\frac{\hbar }{L_{Pl}^2}dR=\frac{dR}{G} | ||
| + | \end{equation} | ||
| + | ($L_{Pl}^2=\hbar G/c^3$). | ||
| + | The quantity $dR$ can be presented in the form | ||
| + | \begin{equation} | ||
| + | \label{HolPr:15_2} | ||
| + | dR=-H\dot{H}R^3dt. | ||
| + | \end{equation} | ||
| + | On other hand, the energy flow through the Hubble sphere can be calculated if one is given the energy-momentum tensor for the substance filling the Universe. Treating the latter as an ideal fluid (see Chapter 2) and using the relation $T_{\mu \nu }=(\rho +p)u_{\mu }u_{\nu }+pg_{\mu \nu },$ one obtains | ||
| + | \begin{equation} | ||
| + | \label{HolPr:15_3} | ||
| + | dE=A\left( \rho +p \right)dt | ||
| + | \end{equation} | ||
| + | Equating (\ref{HolPr:15_1}) and (\ref{HolPr:15_3}) and taking into account (\ref{HolPr:15_2}), one finds | ||
| + | \begin{equation} | ||
| + | \label{HolPr:15_4} | ||
| + | \dot{H}=-4\pi G\left( \rho +p \right). | ||
| + | \end{equation} | ||
| + | As it was shown in Chapter 2, the system of equations | ||
| + | \begin{align} | ||
| + | \nonumber | ||
| + | & \dot{H}=-4\pi G\left( \rho +p \right);\\ | ||
| + | & \dot{\rho }+3H\left( \rho +p \right)=0, | ||
| + | \end{align} | ||
| + | is equivalent to the standard system of Friedman equations | ||
| + | \begin{align} | ||
| + | \nonumber | ||
| + | H^2 = & \frac{8\pi G}{3}\rho ; \\ | ||
| + | \frac{\ddot{a}}{a} = & -\frac{4\pi G}{3}(\rho +3p). | ||
| + | \end{align} | ||
| + | The application of this method to obtain the Friedman equations for a non-flat Universe will be considered in the next problem. | ||
| + | |||
| + | |||
| + | '''2nd method.''' | ||
| + | |||
| + | Consider a compact spatial region $V$ with boundary $\partial V,$ which represents a sphere with physical radius $R=ar.$ The boundary acts as a holographic screen. Assume that the number of bits on the screen equals to | ||
| + | $$ | ||
| + | N=\frac{Ac^3}{G\hbar }, | ||
| + | $$ | ||
| + | and the equipartition theorem gives | ||
| + | $$ | ||
| + | E=Mc^2=\frac{1}{2}Nk_{_B}T. | ||
| + | $$ | ||
| + | In this relation the mass $M$ is equal to the total mass in the region enclosed by the spherical holographic screen. As usual, assume that the matter filling the considered region is ideal fluid with the energy-momentum tensor | ||
| + | $$ | ||
| + | T_{\mu \nu }=\left( p+\rho \right)u_{\mu }u_{\nu }+pg_{\mu \nu }. | ||
| + | $$ | ||
| + | Total mass in the spatial region $V$ is | ||
| + | $$ | ||
| + | M=\int_{V}{dV}\left(T_{\mu \nu }u^{\mu }u^{\nu }\right). | ||
| + | $$ | ||
| + | Here $T_{\mu \nu }u^{\mu }u^{\nu }$ is the energy density measured by the comoving observer with $4$-velocity $u^\mu$. On the other hand, acceleration for radial comoving observer in the point $r,$ i.e. in the point where the screen is situated, equals to | ||
| + | $$ | ||
| + | a_r=\frac{d^2R}{dt^2}=-\ddot{a}r | ||
| + | $$ | ||
| + | The minus sign appears because one considers the acceleration caused by matter in the region enclosed by the screen. According to the Unruh formula (\ref{Hol_f_Unruh:4}), this acceleration corresponds to temperature | ||
| + | $$ | ||
| + | T=\frac{1}{2\pi k_{_B}c}\hbar a_{r}. | ||
| + | $$ | ||
| + | Substitution of the quantities determined above into the equipartition theorem gives | ||
| + | $$ | ||
| + | \ddot{a}=-\frac{4\pi G}{3}\rho a. | ||
| + | $$ | ||
| + | This is nothing else then the Newton analogue of the second Friedman equation. In order to obtain the exact Friedman equation, which follows from General Relativity, one has to use the so-called active gravitational mass | ||
| + | $$ | ||
| + | M^*=2\int_{V}dV\left(T_{\mu \nu }-\frac{1}{2}Tg_{\mu \nu }\right)u^{\mu }u^{\nu }. | ||
| + | $$ | ||
| + | Replacing $M$ by $M^*$, one obtains | ||
| + | $$ | ||
| + | \frac{\ddot{a}}{a}=-\frac{4\pi G}{3}\left( \rho +3p \right) | ||
| + | $$ | ||
| + | Multiplying both sides of the latter equality by $\dot{a}a$ and using the conservation equation | ||
| + | $$ | ||
| + | \dot{\rho }+3H\left( \rho +p \right)=0, | ||
| + | $$ | ||
| + | one obtains the first Friedman equation | ||
| + | $$ | ||
| + | H^2+\frac{k}{a^2}=\frac{8\pi G}{3}\rho. | ||
| + | $$ | ||
| + | Here $k$ is the integration constant, which can be treated as the spatial curvature in the region $V.$</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 294: | Line 515: | ||
| − | <div id=""></div> | + | <div id="HU22"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Derive the Friedman equations from the holographic principle for a non-flat Universe. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Repeat all the steps similar to (\ref{HolPr:15_1}) - (\ref{HolPr:15_4}), using for $R_H$ the expression obtained in problem \ref{equ24n} of Chapter 2 |
| + | \begin{equation} | ||
| + | \label{R_H} | ||
| + | R_H=\frac{1}{\sqrt{H^2+\frac{k}{a^2}}}, | ||
| + | \end{equation} | ||
| + | to obtain | ||
| + | \begin{equation} | ||
| + | \dot{H}=-4\pi G(\rho +p)+\frac{k}{a^2}. | ||
| + | \end{equation} | ||
| + | Combined with the conservation equation, it is equivalent to | ||
| + | \begin{align} | ||
| + | \nonumber | ||
| + | & H^2=\frac{8\pi G}{3}\rho -\frac{k}{a^2}; \label{Fridmann_eq}\\ | ||
| + | & \frac{\ddot{a}}{a}=-\frac{4\pi G}{3}(\rho +3p). \\ | ||
| + | \nonumber | ||
| + | \end{align}</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 307: | Line 543: | ||
| − | <div id=""></div> | + | <div id="HU23"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Consider an effective field theory with the ultraviolet cutoff parameter equal to $\Lambda$ and entropy satisfying the inequality | |
| + | \[S\equiv L^3\Lambda^3\le S_{BH}\simeq L^2 M_{Pl}^2,\] | ||
| + | where $S_{BH}$ is the Beckenstein-Hawking entropy, and show that such a theory necessarily contains the states with Schwarzschild radius $R_S$ much greater than the linear dimensions $L$ of the system. (see Zimdahl, Pavon, 0606555) | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">For sufficiently high temperatures ($T\gg {{L}^{-1}}$, but $T\le \Lambda $) the energy of the system is $E$ $\simeq {{L}^{3}}{{T}^{4}}$, and its entropy $S\simeq {{L}^{3}}{{T}^{3}}$. When the inequality \[S\le {{S}_{BH}}\] is saturated (let us assume that $T=\Lambda $), then $T\simeq {{\left( M_{Pl}^{2}/L \right)}^{1/3}}$. On the other hand, the Schwarzschild radius is related to the energy as ${{R}_{s}}\simeq E/M_{Pl}^{2}$ . Therefore ${{R}_{S}}\gg L$.</p> |
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 320: | Line 558: | ||
| − | <div id=""></div> | + | <div id="HU24"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Estimate the dark energy density assuming that the total energy in a region with linear size $L$ cannot exceed the black hole mass of the same size. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">$$ |
| + | \rho_{_{DE}} \le \frac{c}{2GL^2}. | ||
| + | $$ | ||
| + | Saturation of the inequality is equivalent to the choice of maximum allowed value for $L.$ In cosmological context it is reasonable to chose $L$ equal to the current size of the Universe, i.e. Hubble scale $L\sim H^{-1}$ (the quantities similar to $L$ in holographic physics are called the infrared cutoff scale (IR cutoff)). Then according to the holographic principle $\rho_{_{DE}}\propto H^{2}$ | ||
| + | |||
| + | For $\hbar =c=1$ the restriction formulated in the statement of the problem can be presented in the form | ||
| + | $$ | ||
| + | L^3\rho_{DE}\le LM_{Pl}^{2} | ||
| + | $$ | ||
| + | |||
| + | Saturation of this inequality is equivalent to the choice of maximum allowed value for $L.$ In cosmological context it is reasonable to chose $L$ equal to current size of Universe, i.e. Hubble scale $L\sim H^{-1}.$ Then | ||
| + | $$ | ||
| + | \rho_{DE}\sim H^2M_{Pl}^{2} | ||
| + | $$ | ||
| + | and | ||
| + | \begin{align} | ||
| + | \nonumber | ||
| + | M_{Pl} & \simeq 1.2\times 10^{19} \;\mbox{\it GeV };\\ \nonumber | ||
| + | {{H}_{0}} & \simeq 1.6\times {{10}^{-42}}\;\mbox{\it GeV } \\ \nonumber | ||
| + | \rho_{_{DE}} & \sim 10^{-46}\;\mbox{\it GeV}^{4}. | ||
| + | \end{align} | ||
| + | This value differs only by two orders of magnitude from the observed density of dark energy $\rho _{DE}^{\left( obs \right)}\sim 10^{-48}\;\mbox{\it GeV}^{4}$. Recall that dimensional estimate in the frame of SCM led to divergence of 120(!) orders of magnitude.</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 333: | Line 592: | ||
| − | <div id=""></div> | + | <div id="HU25"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Find the correspondence between the ultraviolet and infrared cutoff scales. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Holographic principle applied to black holes as objects with maximum entropy in a given region of space states that the maximum entropy inside the region is proportional only to the surface area of the region, and the number of independent degrees of freedom is limited by the value of the surface area expressed in Planck units (\ref{Hol_f:1}): |
| + | $$ | ||
| + | N\leq \frac{Ac^3}{G\hbar}. | ||
| + | $$ | ||
| + | Therefore effective quantum field theory with ultraviolet cutoff $\Lambda $ defined in the region of linear size $L,$ with entropy proportional to $S\sim L^3\Lambda^3,$ must satisfy the condition | ||
| + | \begin{equation} | ||
| + | \label{conditionQFT} | ||
| + | L^3\Lambda^3\le S_{BH}\equiv \frac{1}{4}\frac{A}{l_{Pl}^2}=\pi L^2M_{PL}^2 | ||
| + | \end{equation} | ||
| + | where $S_{BH}$ is entropy of black hole of radius $L.$ Thus the latter relation shows that the value of the infrared cutoff (IR cutoff) cannot be chosen independently from the ultraviolet cutoff value: | ||
| + | \begin{equation} | ||
| + | \label{LsimLambda{-3}} | ||
| + | L\sim \Lambda^{-3} | ||
| + | \end{equation} | ||
| + | In other words in quantum field theory the ultraviolet cutoff on small scales is related to the infrared cutoff on large scales (See one of the early works on the topic: Andrew G. Cohena, David B. Kaplanb and Ann E. Nelsonc, Effective Field Theory, Black Holes, and the Cosmological Constant, [http://arxiv.org/abs/hep-th/9803132 arXiv:hep-th/9803132v2 31 Mar 1999]).</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 346: | Line 619: | ||
| − | <div id=""></div> | + | <div id="HU26"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Show that the entropy force produces negative pressure. | |
| − | <div class="NavFrame collapsed"> | + | <!--<div class="NavFrame collapsed"> |
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
<p style="text-align: left;"></p> | <p style="text-align: left;"></p> | ||
</div> | </div> | ||
| − | </div></div> | + | </div>--></div> |
| − | <div id=""></div> | + | <div id="HU27"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Taking the Hubble sphere for the holographic screen, and using the SCM parameters, find the entropy, the force acting on the screen and the corresponding pressure. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Entropy contained on the Hubble sphere is |
| + | \begin{equation} | ||
| + | S_H = \frac{k_B c^3}{G \hbar} \frac{A}{4} = \frac{k_B c^3} {G \hbar} \pi R_H^2 = \frac{k_B c^3} {G \hbar} \pi \left( \frac{c}{H} \right)^2 \sim (2.6 \pm 0.3) \times 10^{122} k_B | ||
| + | \end{equation} | ||
| + | Note that change of Hubble radius $R_H$ by $\Delta r$ causes the entropy change equal to | ||
| + | \begin{equation} | ||
| + | \Delta S_H = \frac{k_B c^3} {G \hbar} 2\pi R_H \Delta r = \frac{k_B c^3} {G \hbar} 2\pi \left( \frac{c}{H} \right) \Delta r \sim (2.6 \pm 0.3) \times 10^{122} k_B \Delta r / R_H. | ||
| + | \end{equation} | ||
| + | The force acting on the holographic screen then is | ||
| + | \begin{equation} | ||
| + | F_r = - \frac{dE}{dr} = - T \frac{dS}{dr} = - T_\beta \frac{ d S_H}{d r} = - \frac{\hbar}{ k_B }~\frac{ H }{ 2 \pi} \frac{k_B c^3} {G \hbar} 2\pi \left( \frac{c}{H} \right) = - \frac{c^4 }{ G}. | ||
| + | \end{equation} | ||
| + | The minus sign points on the fact that the force acts in the direction of expanding of the holographic screen. The corresponding pressure takes the form | ||
| + | \begin{equation} | ||
| + | P = \frac{F_r}{A} = - \frac{1}{A} T \frac{dS}{dr} = - \frac{1}{A} \frac{c^4 }{ G} = - \frac{1}{ 4 \pi c^2/H^2} \frac{c^4 }{ G} = - \frac{c^2 H^2 }{4 \pi G} = - \frac{2}{3} \rho_{cr} c^2, | ||
| + | \end{equation} | ||
| + | where $\rho_{cr}$ is critical energy density, equal to $\rho_{cr} \equiv 3 H^2 /8 \pi G$.</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 372: | Line 661: | ||
| − | <div id=""></div> | + | <div id="HU28"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | The most popular approach to explain the observed accelerated expansion of the Universe assumes introduction of dark energy in the form of cosmological constant into the Friedman equations. As we have seen in the corresponding Chapter, this approach is successfully realized in SCM. Unfortunately, it leaves aside the question of the nature of the dark energy. An alternative approach can be developed in the frame of holographic dynamics. In this case it is possible to explain the observations without the dark energy. It is replaced by the entropy force, acting on the cosmological horizon (Hubble sphere) and leading to the accelerated Universe's expansion. | |
| + | <br/> | ||
| + | Show that the Hubble sphere acceleration obtained this way agrees with the result obtained in SCM. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">As shown in SCM (see problem \ref{SCM6} of Chapter 11), acceleration of an object situated on distance $R$ from the observer equals to |
| + | $$ | ||
| + | \dot{V}=H_{0}^{2}\left( \Omega_{\Lambda }-\frac{1}{2}\Omega_{m}\right)R. | ||
| + | $$ | ||
| + | For $R=4000\;\mbox{\it Mpc}$ (size of the observable Universe), $\dot{V}\simeq 4\times {{10}^{-10}}\;\mbox{\it m/sec}^2.$ | ||
| + | Using the solution of problem \ref{HU12} of the present Chapter, one can find that acceleration of the Hubble sphere equals to | ||
| + | $$ | ||
| + | a_{_H}=\frac{2\pi ck_{_B}}{\hbar }T_{U}(a=g)=cH_0\simeq 10^{-9}\;\mbox{\it m/sec}^2. | ||
| + | $$ | ||
| + | This results agrees by the order of magnitude with the previously obtained estimate in the frame of SCM.</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 385: | Line 685: | ||
| − | <div id=""></div> | + | <div id="HU29"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
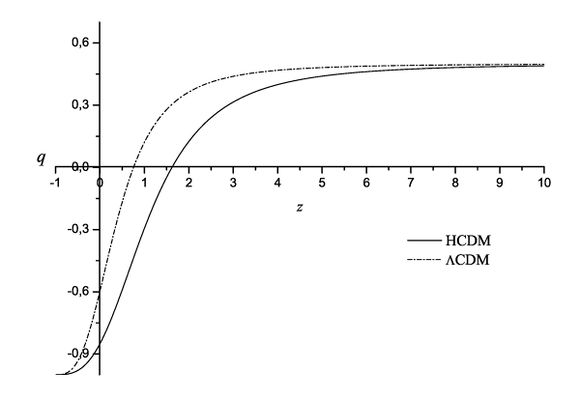
| − | + | Plot the dependence of the deceleration parameter on the red shift in the Universe composed of non-relativistic matter. Take into account the negative pressure generated by the entropy force (see Problem \ref{HU26}). Compare the result with the SCM. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">The easiest way to take into account the negative pressure generated by the entropic force is to modify the right hand side of the second Friedman equation by addition of a corresponding term. In order to do that one can use dimensional considerations, which results in the following relation |
| + | \begin{equation} | ||
| + | \frac{\ddot a}{a}=-\frac{4\pi G}{3}(\rho+3p)+\frac{a_e}{R_b}. | ||
| + | \end{equation} | ||
| + | Note that distance to the holographic screen does not have to coincide with the Hubble radius, therefore it is reasonable to choose the holographic screen with the radius | ||
| + | \begin{equation} | ||
| + | R_b=\frac{1}{\beta H}, | ||
| + | \end{equation} | ||
| + | and corresponding temperature of the holographic screen takes the form | ||
| + | \begin{equation} | ||
| + | T_H=\frac{\beta H}{2\pi}. | ||
| + | \end{equation} | ||
| + | Thus the modified equation becomes | ||
| + | \begin{equation} | ||
| + | \label{Fridmann_eqIIm} | ||
| + | \frac{\ddot a}{a}=-\frac{4\pi G}{3}(\rho+3p)+\beta^2H^2. | ||
| + | \end{equation} | ||
| + | The deceleration parameter depends on the redshift as | ||
| + | $$ | ||
| + | q(z) = -1 +\frac{1+z}{H(z)}\frac{dH}{dz} | ||
| + | $$ | ||
| + | (see the picture). | ||
| + | <gallery widths=600px heights=400px> | ||
| + | File:q_z.jpg|Dependence of deceleration parameter on the redshift for the case of $1)$ Universe with holographic dark energy $HCDM$ (solid line); $2)$ Standard cosmological model $\Lambda CDM$ (dashed line). | ||
| + | </gallery> | ||
| + | |||
| + | In The frame of $\Lambda CDM$ the dependence of deceleration parameter on redshift is determined by | ||
| + | $$ | ||
| + | q = \frac{1}{2}\frac{\Omega _M^{(0)}(1 + z)^3- 2\Omega _\Lambda ^{(0)}} | ||
| + | {\Omega _M^{(0)}(1 + z)^3+\Omega_\Lambda ^{(0)}}, | ||
| + | $$ | ||
| + | where $\Omega _M^{(0)}$ and $\Omega_\Lambda ^{(0)}$ are relative densities of non-relativistic matter and cosmological constant respectively. | ||
| + | Recall that in the frame of $\Lambda CDM$ one usually takes | ||
| + | $ | ||
| + | \Omega _M^{(0)} = 0.27,[[User:Cosmo All|Cosmo All]] \Omega_\Lambda ^{(0)}=0.73. | ||
| + | $ | ||
| + | The presented plots demonstrate both good qualitative and quantitative agreement between holographic dark energy model ($HCDM$) and $\Lambda CDM$: both models give the same asymptotes and similar behavior near the intersection with the $z$-axis: | ||
| + | $$ | ||
| + | q(z \to \infty ) = \frac{1}{2},[[User:Cosmo All|Cosmo All]]\;q(z \to - 1) = - 1. | ||
| + | $$</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 398: | Line 737: | ||
| − | <div id=""></div> | + | <div id="HU30"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Show that the coincidence problem does not arise in the models with the holographic dark energy. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">As shown above (see [[#HU24 | problem]]), the holographic dark energy can be presented in the form |
| + | $$ | ||
| + | \rho_{_{HDE}} = \alpha^2H^2. | ||
| + | $$ | ||
| + | Consider Universe composed of non-relativistic matter and holographic dark energy | ||
| + | \begin{align} | ||
| + | H^2= & \frac 13 \left(\rho_{m}+\rho_{_{HDE}}\right);\\ | ||
| + | \frac{3-\alpha^2}{\alpha^2}= & \frac{\rho_{m}}{\rho_{_{HDE}}} = const. | ||
| + | \end{align} | ||
| + | Thus the ratio of both densities remains constant during all evolution of the Universe, which solves the coincidence problem (but produces another problem, see the next problem).</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 411: | Line 759: | ||
| − | <div id=""></div> | + | <div id="HU31"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Show that the holographic screen in the form of Hubble sphere cannot explain the accelerated expansion of Universe. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Consider a Universe dominated by holographic dark energy: |
| + | $$ | ||
| + | \rho_{_{HDE}} = \alpha^2H^2. | ||
| + | $$ | ||
| + | Use the conservation equation $\dot{\rho}+3H\left( \rho +p\right)=0,~p=w\rho$ | ||
| + | \begin{equation} | ||
| + | w = -1- \frac{1}{ 3}\frac{d\ln\rho}{d\ln a} = -\frac{1}{3}. | ||
| + | \end{equation} | ||
| + | Take into account the second Friedman equation | ||
| + | $$\frac{\ddot a}{a}=-\frac{4\pi G}{3}(\rho+3p).$$ | ||
| + | to obtain the result that $\ddot a = 0.$</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 424: | Line 782: | ||
| − | <div id=""></div> | + | <div id="HU32"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Find the dependence of holographic dark energy density on the scale factor taking the cosmological particle horizon $R_p$ as the holographic screen. Show that such choice cannot explain the accelerated expansion of the Universe. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">\begin{align}\nonumber |
| + | \rho_{_{HDE}} & =3c^2M_p^2L^{-2},\\ \nonumber | ||
| + | H^2 & =\frac{1}{3M_p^2}\rho. | ||
| + | \end{align} | ||
| + | Consider Universe composed of holographic dark energy | ||
| + | $$ | ||
| + | H^2=c^2L^{-2} | ||
| + | $$ | ||
| + | and use the definition | ||
| + | \begin{equation}\nonumber | ||
| + | R_p = a\int^a_0 \frac{da'}{H(a')a'^2}. | ||
| + | \end{equation} | ||
| + | Then take into account the relation $L=R_p$ to obtain | ||
| + | $$ | ||
| + | HR_p = c, | ||
| + | $$ | ||
| + | and therefore | ||
| + | $$ | ||
| + | \frac{1}{Ha^2}=c\frac{d}{ da}\left(\frac{1}{ Ha}\right). | ||
| + | $$ | ||
| + | It then follows that | ||
| + | $$H^{-1}=\alpha a^{1+\frac{1}{c}}.$$ | ||
| + | Thus in the case when the holographic screen coincides with the cosmological particle horizon the holographic dark energy density depends on the scale factor as | ||
| + | $$ | ||
| + | \rho_{_{HDE}}=3c^2\alpha^{-2} M_p^2 a^{-2(1+\frac{1}{c})}. | ||
| + | $$ | ||
| + | Use the conservation equation $\dot{\rho}+3H\left( \rho +p\right)=0,~p=w\rho$ to obtain | ||
| + | $$ | ||
| + | w = -1- \frac{1}{ 3}\frac{d\ln\rho}{d\ln a} = -\frac{1}{ 3}+\frac{2}{ 3c}>-\frac{1}{3} | ||
| + | $$ | ||
| + | Thus the given cosmological model is unable to provide the accelerated expansion of the Universe.</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 437: | Line 825: | ||
| − | <div id=""></div> | + | <div id="HU33"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Obtain the equation of motion for the relative density of the holographic dark energy in the case when the particle horizon serves as the holographic screen. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">The particle horizon is defined as |
| + | \begin{equation} | ||
| + | R_{p}=a(t)\int^{t}_{0}\frac{dt'}{a}=a\int^{a}_{0}\frac{da'}{Ha'^{2}}. | ||
| + | \end{equation} | ||
| + | After the algebra analogous to that of problem (\ref{HU36}), one obtains | ||
| + | \begin{equation} | ||
| + | \Omega_{\Lambda}'=\Omega_{\Lambda}\left(1-3\Omega_{\Lambda}-\frac{2}{c}\sqrt{\Omega_{\Lambda}}\right),\label{eq:PHEQ} | ||
| + | \end{equation}</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 450: | Line 845: | ||
| − | <div id=""></div> | + | <div id="HU34"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Solve the equation of motion obtained in the previous problem. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">Solution of the equation reads |
| + | \begin{align} \nonumber | ||
| + | \frac{1}{\sqrt{1+3c^2}}\big[\ln\left(\sqrt{1+3c^2}+1+3c\sqrt{\Omega_\Lambda}\right) | ||
| + | & -\ln\left(1+3c\sqrt{\Omega_\Lambda}-\sqrt{1+3c^2}\right)\big]\\ | ||
| + | +\ln\Omega_{\Lambda}-\ln\left(3c\Omega_{\Lambda}+2\sqrt{\Omega_{\Lambda}}-c\right) | ||
| + | & =-\ln a+D_0, \\ | ||
| + | D_0 =\ln\Omega_{\Lambda0}-\ln\left(3c\Omega_{\Lambda0}+2\sqrt{\Omega_{\Lambda0}}-c\right) & \\ \nonumber | ||
| + | +\frac{1}{\sqrt{1+3c^2}}\big[\ln\left(\sqrt{1+3c^2}+1+3c\sqrt{\Omega_{\Lambda0}}\right) | ||
| + | & -\ln\left(1+3c\sqrt{\Omega_{\Lambda0}}-\sqrt{1+3c^2}\right)\big], | ||
| + | \end{align} | ||
| + | where the integration constant $D_0$ is defined by the condition $a_0=1$.</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 463: | Line 868: | ||
| − | <div id=""></div> | + | <div id="HU35"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Find dependence the of holographic dark energy density on the scale factor taking the cosmological event horizon $R_h$ as the holographic screen. Find the equation of state parameter for such a dark energy. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">The event horizon limits the current region of the Universe, from which the information can reach us during time $t_{max}$ in the future |
| + | $$ | ||
| + | R_h =a(t)\int^{t_{max}}_t \frac{dt'}{a(t')}. | ||
| + | $$ | ||
| + | Usually one takes $t_{max}$ equal either to $t=\infty$ or the time when the closed Universe collapses. In the latter case | ||
| + | $$ | ||
| + | HR_h = c, | ||
| + | $$ | ||
| + | and therefore | ||
| + | $$ | ||
| + | H = \alpha a^{-(1-\frac{1}{c})}. | ||
| + | $$ | ||
| + | Thus in the case when the holographic screen coincides with the cosmological event horizon the holographic dark energy density depends on the scale factor as | ||
| + | $$ | ||
| + | \rho_{_{HDE}}=3c^2\alpha^{-2} M_p^2 a^{-2(1-\frac{1}{c})}. | ||
| + | $$ | ||
| + | $$ | ||
| + | w = -1- \frac{1}{ 3}\frac{d\ln\rho}{d\ln a} = -\frac{1}{3}-\frac{2}{ 3c}<-\frac{1}{ 3}. | ||
| + | $$ | ||
| + | The case $c = 1$ corresponds to the cosmological constant with $w=-1.$</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 476: | Line 900: | ||
| − | <div id=""></div> | + | <div id="HU36"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Obtain the equation of motion for the relative density of the holographic dark energy in the case when the event horizon serves as a holographic screen. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">The cosmological horizon is |
| + | \begin{equation} | ||
| + | R_{h}=a\int^{\infty}_{t}\frac{dt'}{a}=a\int^{\infty}_{a}\frac{da'}{Ha'^{2}}\label{eq:eh} | ||
| + | \end{equation} | ||
| + | and the holographic dark energy densities takes the form | ||
| + | \begin{equation} | ||
| + | \rho_{\Lambda}=3c^2M^2_P/L^2_h.\label{eq:ehvv} | ||
| + | \end{equation} | ||
| + | Using the definitions of relative energy density | ||
| + | $\Omega_{m}=\rho_{m}/(3M^2_PH^2)$ and | ||
| + | $\Omega_{\Lambda}=\rho_{\Lambda}/(3M^2_PH^2)$ and the following relation between them | ||
| + | \begin{equation} | ||
| + | \Omega_{m}+\Omega_{\Lambda}=1, | ||
| + | \end{equation} | ||
| + | one can obtain the logarithmic derivative of the Hubble parameter with respect to the scale factor's logarithm | ||
| + | \begin{equation} | ||
| + | \frac{d\ln | ||
| + | H}{d\ln a}+\frac{3}{2}\left(1-\Omega_{\Lambda}\right)=0.\label{eq:diffH} | ||
| + | \end{equation} | ||
| + | Combine (\ref{eq:eh}), (\ref{eq:ehvv}) and the definition of | ||
| + | $\Omega_{\Lambda}$ to obtain | ||
| + | \begin{equation} | ||
| + | \int^{\infty}_{a}\frac{d\ln | ||
| + | a'}{Ha'}=\frac{c}{aH}\sqrt{\frac{1}{\Omega_{\Lambda}}}.\label{eq:integral} | ||
| + | \end{equation} | ||
| + | take derivative by $\ln a$ of both sides of the equation (\ref{eq:integral}) to get | ||
| + | \begin{equation} | ||
| + | \frac{d\ln | ||
| + | H}{dx}+\frac{1}{2}\frac{d\ln\Omega_{\Lambda}}{dx}=\frac{\sqrt{\Omega_{\Lambda}}}{c}-1.\label{eq:Hdx} | ||
| + | \end{equation} | ||
| + | Substitute (\ref{eq:diffH}) into the equation (\ref{eq:Hdx}) to obtain | ||
| + | $\Omega_{\Lambda}$ | ||
| + | \begin{equation} | ||
| + | \frac{d\Omega_{\Lambda}}{d\ln a}=\Omega_{\Lambda}\left(1-3\Omega_{\Lambda}+\frac{2}{c}\sqrt{\Omega_{\Lambda}}\right),\label{eq:EHEQ} | ||
| + | \end{equation}</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 489: | Line 947: | ||
| − | <div id=""></div> | + | <div id="HU37"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
| − | + | Solve the equation of motion obtained in the previous problem. | |
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">The equation can be solved exactly |
| + | \begin{align}\nonumber | ||
| + | \frac{1}{\sqrt{1+3c^2}}\big[\ln\left(\sqrt{1+3c^2}+1-3c\sqrt{\Omega_{\Lambda}}\right) | ||
| + | - \ln\left(\sqrt{1+3c^2}-1+3c\sqrt{\Omega_{\Lambda}}\right)\big] & \\ | ||
| + | +\ln\Omega_{\Lambda} - \ln\left(2\sqrt{\Omega_{\Lambda}}+c-3c\Omega_{\Lambda}\right) | ||
| + | & =\ln a+C_0, | ||
| + | \end{align} | ||
| + | \begin{align}\nonumber | ||
| + | C_0 & = \ln\Omega_{\Lambda0} -\ln\left(2\sqrt{\Omega_{\Lambda0}}+c-3c\Omega_{\Lambda0}\right)\\ \nonumber | ||
| + | & +\frac{1}{\sqrt{1+3c^2}}\big[\ln\left(\sqrt{1+3c^2}+1-3c\sqrt{\Omega_{\Lambda0}}\right) | ||
| + | -\ln\left(\sqrt{1+3c^2}-1+3c\sqrt{\Omega_{\Lambda0}}\right)\big] | ||
| + | \end{align} | ||
| + | where the integration constant $C_0$ can be determined from the condition $a_0=1$.</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
| Line 502: | Line 972: | ||
| − | <div id=""></div> | + | <div id="HU38"></div> |
<div style="border: 1px solid #AAA; padding:5px;"> | <div style="border: 1px solid #AAA; padding:5px;"> | ||
=== Problem 1: === | === Problem 1: === | ||
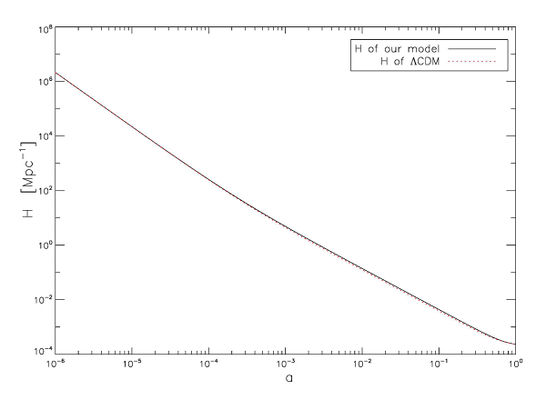
| − | + | Find the dependence of cosmological parameters (Hubble parameter $H$, state equation parameter $w$ and deceleration parameter $q$) on red shift in the model of | |
| + | the Universe composed of radiation, non-relativistic matter and | ||
| + | holographic dark energy, taking as the holographic screen the Ricci | ||
| + | scalar's $R$ characteristic length | ||
| + | $$ | ||
| + | \rho_{_{RDE}}=-\frac{\alpha}{16\pi} R | ||
| + | =\frac{3\alpha}{8\pi}\left(\dot{H}+2H^2+\frac{ k}{a^2}\right), | ||
| + | $$ | ||
| + | where $\alpha $ is a positive constant, $k $ is the sign of space | ||
| + | curvature. | ||
<div class="NavFrame collapsed"> | <div class="NavFrame collapsed"> | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">By definition |
| + | $$ | ||
| + | \rho_{_{RDE}}=-\frac{\alpha}{16\pi} R =\frac{3\alpha}{8\pi}\left(\dot{H}+2H^2+\frac{ | ||
| + | k}{a^2}\right). | ||
| + | $$ | ||
| + | Introducing the notation $x=\ln (1+z)$, one can transform the first Friedman equation to | ||
| + | \begin{eqnarray} | ||
| + | H^2&=&\frac{8\pi}{3}\left[{{\left(\alpha | ||
| + | -1\right)\frac{3k}{8\pi}}}{e^{2x}}+{\rho_{m}}{e^{3x}}+{\rho_{r}}{{e^{4x}}}\right]\nonumber\\ | ||
| + | &&+\alpha\left(2H^2 - \frac{1}{2}\frac{dH^2}{dx}\right), | ||
| + | \end{eqnarray} | ||
| + | where $\rho_m$ and $\rho_{r}$ are densities of non-relativistic and relativistic matter respectively. The deceleration parameter is obtained in the same way. | ||
| + | <br/> | ||
| + | Evolution of the deceleration parameter is described by | ||
| + | \[q=-\frac{{\ddot{a}}}{a{{H}^{2}}}=\frac{\frac{4\pi G}{3}\left( {{\rho }_{tot}}+3{{p}_{tot}} \right)}{\frac{8\pi G}{3}{{\rho }_{tot}}}=\frac{1}{2}+\frac{3}{2}\frac{{{p}_{tot}}}{{{\rho }_{tot}}}\] | ||
| + | Use the dependencies of density and pressure on scale factor (redshift), obtained in previous problems, to obtain the results presented on Fig.\ref{fig:HolPr24_3-4}. | ||
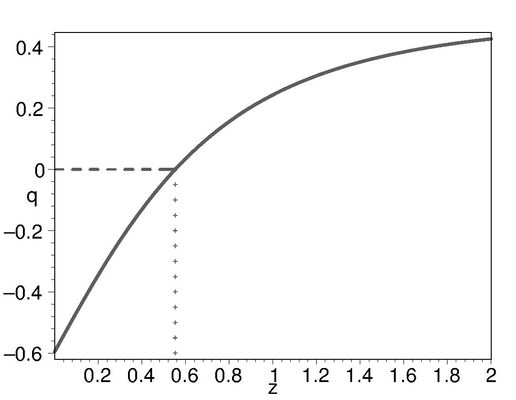
| + | <br/> | ||
| + | Acceleration of Universe's expansion starts at $z\simeq 0.55.$ (Compare with the combined analysis of $SNe+CMB$ data with the $\Lambda CDM$, resulting in $z=0.52\div 0.73$) | ||
| + | <gallery widths=600px heights=400px> | ||
| + | File:evolutionH.jpg|The Hubble parameter for the case of Universe composed of holographic dark energy with scalar Ricci curvature. | ||
| + | </gallery> | ||
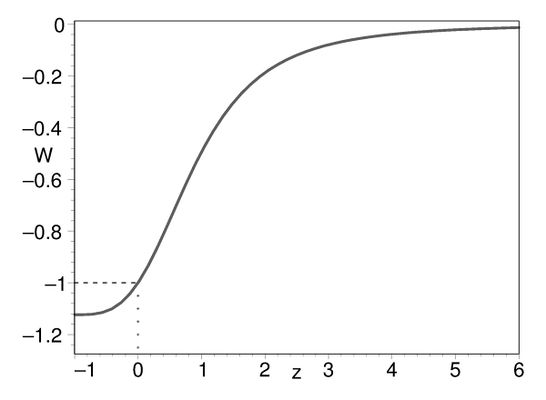
| + | <gallery widths=600px heights=400px> | ||
| + | File:w-z.jpg| | ||
| + | File:q-z.jpg| | ||
| + | </gallery> | ||
| + | State equation parameter $w(z)$ and deceleration parameter $q(z)$ for the case of Universe composed of holographic dark energy with Ricci scalar curvature. | ||
| + | |||
| + | |||
| + | This model is usually called the holographic dark energy with scalar Ricci curvature (see Changjun Gao, Fengquan Wu, and Xuelei Chen, A Holographic Dark Energy Model from Ricci Scalar Curvature - arXiv:0712.1394v4 [astro-ph] 25 Dec 2008 ).</p> | ||
</div> | </div> | ||
</div></div> | </div></div> | ||
Revision as of 21:09, 28 March 2013
Problem 1:
Show that information density on holographic screen is limited by the value $\sim 10^{69} \: \mbox{bit/m}^2.$
Problem 2:
Choosing the Hubble sphere as a holographic screen, find its area in the de Sitter model (recall that in this model the Universe dynamics is determined by the cosmological constant $\Lambda >0$).
$$ A=\frac{12\pi }{\Lambda }. $$
Problem 3:
Find the entropy of a quantum system composed of $N$ spin-$1/2$ particles.
Entropy of a quantum system equals to logarithm of the number of degrees of freedom $N,$ i.e. to logarithm of the dimension $\dim H$ of the Hilbert space $$ S=\ln N=\ln (\dim H). $$ For the system of $N$ spin-$1/2$ particles $\dim H = 2^N$ and $$ S=N\ln 2. $$
Problem 4:
Consider a 3D lattice of spin-$1/2$ particles and prove that entropy of such a system defined in a standard way is proportional to its volume.
Let the lattice occupy volume ${{L}^{3}}$, and its spatial period equals to $l$. Entropy of the system is proportional to the number of (quantum) states $N={{2}^{n}},\ n={{\left( \frac{L}{l} \right)}^{3}}$. Therefore \[S\propto \ln N\propto {{\left( \frac{L}{l} \right)}^{3}}\propto V.\]
Problem 5:
Find the change of the holographic screen area when it is crossed by a spin-$1/2$ particle.
Let all the punctures of the holographic screen be due its crossing by spin-$1/2$ particles. Then for $N$ punctures $$ N=\frac{A{{c}^{3}}}{4G\hbar \ln 2}. $$ The crossing leads to an additional puncture and therefore to change of the surface area equal to $$ \Delta A=\frac{\hbar G}{{{c}^{3}}}4\ln 2. $$
Problem 6:
What entropy change corresponds to the process described in the previous problem?
$\Delta S=\ln 2$ (see problem).
Problem 1:
According to Hawking, black holes emit photons (the black hole evaporation) with thermal spectrum and effective temperature $$ T_{BH}=\frac{\hbar c}{4\pi k_{_B}}r_{g}, $$ where $r_{g}={2GM}/{c^2}$ is the black hole Schwarzschild radius. Neglecting accretion and CMB absorption, determine the life time of a black hole with initial mass $M_{0}.$ Calculate the lifetime for black holes with the mass equal to Planck mass, mass of the Earth and Solar mass.
The black hole mass changes due to evaporation according to $$ \frac{dM}{dt}=-\frac{\sigma T_{H}^4A_{BH}}{c^2}, $$ where \[\sigma =\frac{\pi^2k_{_B}^4}{60\hbar^3c^2}\] is the Stefan-Boltzmann constant, and $A_{BH}=4\pi r_g^2$ is the surface area of the black hole. Therefore $$M(t)=\frac{M_{0}}{(1-t/\tau )^{1/3}},$$ where the lifetime of the black hole equals to $$\tau =\frac{5120\pi G^2M_{0}^3}{\hbar c^4}.$$ Characteristic lifetimes are the following: \[[[:Template:\left. \tau \right]]=5120\pi {{t}_{Pl}}\sim {{10}^{-39}}s,\] \[[[:Template:\left. \tau \right]]\sim {{10}^{58}}c\sim {{10}^{50}}\;\mbox{\it years,}\] \[[[:Template:\left. \tau \right]]\sim {{10}^{75}}c\sim {{10}^{67}}\;\mbox{\it years.}\]
Problem 1:
Show that black holes have negative thermal capacity.
The black hole entropy has the form \[S_{BH}=\frac{M_{Pl}^2}{16\pi k_B T^2},\] its temperature equals to \[T_{BH}=\frac{M_{Pl}^2}{8\pi k_BM},\] then its thermal capacity is \begin{equation} \label{C_{BH}} C_{BH}=T\left( \frac{\partial S}{\partial T}\right)=-8\pi k_B\frac{M^2}{M_{Pl}^2}. \end{equation}
Problem 1:
Show that the black hole evaporation process is accompanied by increase of its temperature. Find the relative variation of the black hole temperature if its mass gets twice smaller due to evaporation.
When the black hole mass is halved, its temperature becomes twice as high.
Problem 1:
Show that in order to produce an entropy force when a particle approaches the holographic screen, its temperature must be finite.
Temperature is defined as $$ \frac{dS}{dE}=\frac{1}{T}. $$ Any motion of a particle (or propagation of excitation) leads to entropy change $\Delta S\sim \Delta x$ and therefore to change of energy. Thus the screen temperature must be finite by definition. In other words, the relation $\Delta E=T\Delta S$ can hold only at finite temperatures.
Problem 1:
Determine the entropic acceleration of a particle crossing the holographic screen with temperature ${{T}_{b}}$.
$$ a_e=\frac{F_e}{m}=T_b\frac{\Delta S}{\Delta x}=2\pi T_b\frac{k_{_B}c}{\hbar}. $$
Problem 1:
Show that the Unruh temperature is the Hawking radiation temperature $$T_{BH}=\frac{\hbar c^3}{8\pi k_{_B}GM}$$ with substitution $a\to g,$ where $g$ is the surface gravity of the black hole.
Substitute the relation $GM=gr_{g}^2$ into the formula for the hawking radiation temperature and take into account the definition of gravity radius $r_{g}=\frac{2MG}{c^2}$=$\frac{c^2}{2g},$ to obtain $$ T_{BH}=\frac{\hbar g}{2\pi k_{_B}c}=T_{_U}(a=g). $$
Problem 1:
In order to verify experimentally the Unruh effect, it is planned to accelerate particles with acceleration of the order of $10^{26} \mbox{\it m/}\sec^2$. What vacuum temperature does this acceleration correspond to?
$$ T_{_U}(a={10^{26}} \mbox{\it m/s}^{2})\simeq 4\times 10^5 K. $$
Problem 1:
Derive the second Newton's law from the holographic principle.
Entropic force acting on a test particle of mass $m,$ which approaches the holographic screen with temperature $T$, equals to $$ F=T\frac{\Delta S}{\Delta x}=2\pi {{k}_{_B}}\frac{mc}{\hbar }T. $$ Treating the temperature $T$ as the Unruh one (see \ref{Hol_f_Unruh:4}) $$ T=\frac{1}{2\pi {{k}_{_B}}}\frac{\hbar }{c}a, $$ one obtains the second Newton's law $$ F=ma. $$
Problem 1:
Show that the inertia law can be obtained from the holographic principle.
Consider a particle of mass $m,$ approaching the holographic screen. At some moment the particle must merge with the microscopic degrees of freedom on the screen, and thus it will consist of the same $n$ bits, like those living on the screen. As every bit transmits energy equal to $\frac{1}{2}{{k}_{B}}T,$ the following must hold $$ mc^2=\frac{1}{2}nk_{_B}T. $$ Substitute the mass into the expression for the entropic force and make use the definition of the Unruh temperature (\ref{Hol_f_Unruh:4}) to express the entropy change in terms of the acceleration $$ \frac{\Delta S}{n\Delta x}=k_{_B}\frac{a}{2c^2}. $$ The obtained equation represents the holographic version of the inertia law: if entropy gradients are absent, then the entropic forces are zeros and as a consequence the acceleration of the particle equals to zero.
Problem 1:
Obtain the Newton's law of universal gravitation using the holographic principle.
Consider a particle of mass $m$ approaching the holographic screen. The particle feels the entropic force $$ F=T\frac{\Delta S}{\Delta x}=2\pi Tk_{_B}\frac{mc}{\hbar }, $$ where $T$ is the holographic screen temperature. Make use of the equipartition theorem $$ E=\frac{1}{2}N k_{_B}T. $$ Here $N$ is the number of degrees of freedom on the screen, which according to the holographic principle equals to (more precisely, cannot exceed) $$ N=\frac{Ac^3}{G\hbar }=\frac{4\pi R^2 c^3}{G\hbar }. $$ Treating $E$ as $M{{c}^{2}},$ where $M$ is the mass concentrated in the region which is enclosed by the holographic screen, one obtains the temperature $$ T=\frac{Mc^2}{2k_{_B}\pi R^2}\frac{G\hbar }{c^3}. $$ Then substitute the obtained temperature into the original expression for the entropic force to recover the Newton's law of universal gravitation $$ F=G\frac{mM}{R^2}. $$
Problem 1:
Compare how close to a black hole are Earth, Sun and observable Universe.
Compare the (Schwarzschild) gravity radii $r_{g}$ and the physical ones $R$ for the Earth and the Sun. For the latter $R\simeq 7\times 10^5 \mbox{\it km},$ and $r_g\simeq 3\mbox{\it km}.$ For the Earth $R\simeq 6400 \mbox{\it km},$ and $r_g\simeq 3\mbox{\it cm}.$ Thus those objects are not similar at all to a black hole. Analogous estimate for the observable part of the Universe enclosed by the Hubble sphere with the radius $R_{H}=c H^{-1}$, gives $$ \begin{gathered} r_{g,univ}=\frac{2GM_{univ}}{c^2}; \hfill \\ R_{H}=cH^{-1}; \\ M_{univ}=\frac{4\pi }{3}R_H^{3}\rho ; \hfill \\ H^2=\frac{8\pi G}{3}\rho \to \rho =\frac{3H^2}{8\pi G}; \hfill \\ M_{univ}=\frac{4\pi }{3}R_H^3\frac{3H^2}{8\pi G}=\frac{c^2R_H}{2G}; \\ R_H=\frac{2GM_{univ}}{c^2}=r_{g,univ}. \hfill \\ \end{gathered} $$ It is this impressive "coincidence" which allows us to use the argumentation of black hole thermodynamics for the holographic description of the Universe.
Problem 1:
Estimate the temperature of the Hubble sphere, considering it as a holographic screen.
To obtain the required estimate, make use of the "similarity" of the observed Universe to a black hole (see the previous problem). The spectrum of the Hawking radiation for massless fields appeared to coincide with the black body radiation, which allows one to assign to the black hole the temperature $$ T_{BH}=\frac{\hbar c^3}{8\pi Gk_{_B}M} $$ Transform this formula using the first Friedman equation $$ T_{BH}=\frac{\hbar c^3}{8\pi Gk_{_B}M}=\frac{1}{3}\frac{\hbar c^3}{k_B}\frac{\rho }{MH^2}=\frac{1}{3}\frac{\hbar c^3}{k_{_B}}\frac{1}{VH^2}. $$ Substitute \[V=\frac{4\pi }{3}R_{H}^3\] and take into account that the Hubble radius equals to $R_{H}=cH^{-1}$ to obtain the temperature of the Hubble sphere \begin{equation} \label{T_{H-univ}} T_{H}=\frac{\hbar H}{4\pi k_{_B}}\sim 10^{-30}\:K. \end{equation}
Problem 1:
Show that equilibrium between the relic radiation and holographic screen is possible only at Planck temperature.
Temperature of the radiation-dominated Universe depends on time as \begin{equation} T=\left( \frac{3}{32\pi G\alpha } \right)^{1/4}t^{-1/2}, \end{equation} where $\alpha $ is constant ($\rho =\alpha T^4$.) Combine the latter expression with the formula (\ref{T_{H-univ}}) and take into account that $H=\left( 2t \right)^{-1}$ for radiation, to obtain $$ T_{H}=\frac{\hbar }{8\pi k_{_B}}\left( \frac{32\pi G\alpha }{2} \right)^{1/2}T_{CMB}^{2}\sim T_{CMB}^{2}\sqrt{G}\simeq \frac{T_{CMB}^{2}}{T_{Pl}} $$ where ${{T}_{Pl}}={{\left( \hbar {{c}^{5}}/Gk_{B}^{2} \right)}^{1/2}}=1.4\cdot {{10}^{32}}K$ is the Planck temperature. Note that the obtained expression is valid for any stage of Universe's evolution, because its temperature is always mostly determined by radiation. Temperature of the matter relaxes to that of radiation, as the thermal capacity of the latter is considerably higher. Therefore according to relation (\ref{T_{H-univ}}) the equilibrium between the relic radiation and the holographic screen is possible only at the Planck temperature.
Problem 1:
According to the holographic ideology, all physical phenomena can be described by the boundary layer theory. Therefore a conclusion comes that one should account for contribution of such surface terms while deriving the equations of General Relativity. Show that consideration of the boundary terms in the Einstein-Hilbert action is equivalent to introduction of non-zero energy-momentum tensor into the standard Einstein equations.
Action for the gravitational field is \begin{equation} S_{EH} \,=\,- \frac{c^{3}}{16 \pi G} \int d^{4} x \,\sqrt{-g} \,R\, . \label{2.1} \end{equation} Variation of the action with respect to metric $g_{\mu \nu}$ (see problem $25$ of Chapter 2) in a compact region $\Omega$ gives \begin{eqnarray} \lefteqn{ \delta \int_{\Omega} d^{4}x \sqrt{-g}\, R \, =} \nonumber \\ & & \int_{\Omega}d^{4} x \sqrt{-g} \Biggl[ \left( g^{\mu \nu}\nabla^2 \delta g_{\mu \nu}\,- \nabla^{\mu} \nabla^{\nu} \delta g_{\mu \nu} \right) -\left( R^{\mu \nu} - \frac{1}{2}\, g^{\mu \nu} R \right) \delta g_{\mu \nu} \Biggr] \, , \label{2.2} \end{eqnarray} where $\nabla^2 \,=\, g^{\alpha \beta} \nabla_{\alpha} \, \nabla_{\beta}$. The functional $S_{Boundary}[g],$ thus takes the form \begin{equation} \delta S_{Boundary}[g]\,=\,-\, \frac{1}{16 \pi G} \int_{\Omega}d^{4}x \sqrt{-g} \Bigl( g^{\mu \nu} \nabla^2 \delta g_{\mu \nu}\,-\, \nabla^{\mu} \nabla^{\nu} \delta g_{\mu \nu} \Bigr) \, , \label{2.4} \end{equation} The Einstein equations including the contribution of boundary terms take the form \begin{eqnarray} R^{\mu \nu} - \frac{1}{2}\, g^{\mu \nu} R = 8 \pi G\, T^{\mu \nu}_{Boundary}\, , \nonumber \\ T^{\mu \nu}_{Boundary} = \frac{2}{\sqrt{- g}} \, \frac{\delta S_{Boundary}} {\delta g_{\mu \nu}}\,. \label{2.5} \end{eqnarray} Note that in the case of flat space-time with $g_{\mu \nu}=const,$ the boundary action $S_{Boundary}[g] = 0,$ and the Einstein equation take the standard form.
Problem 1:
Derive the Friedman equations from the holographic principle.
1st method. As shown in problem \ref{HU17} of the present Chapter, one can use the argumentation of black hole thermodynamics for the holographic description of the Universe. Let the holographic screen coincide with the Hubble sphere (the sphere of radius $R=H^{-1}$). The screen has area $A=4\pi R^2$ and carries the (maximum) information $N=4\pi R^2/L_{Pl}^{2}\; \mbox{bit.}$ Change of information $dN$ during time $dt$, which corresponds to expansion of the Universe from $R$ to $R+dR$, equals to $$ dN=\frac{dA}{L_{Pl}^2}=\frac{8\pi R}{L_{Pl}^2}dR. $$ Here $c=k_{_B}=1.$ Increase of the Hubble radius leads to the change of the Hawking temperature ($T=\hbar/(2\pi R)$) by $$ dT=-\frac{\hbar }{2\pi R^2}dR. $$ From the equipartition theorem \begin{equation} \label{HolPr:15_1} dE=\frac{1}{2}NdT+\frac{1}{2}TdN=\frac{\hbar }{L_{Pl}^2}dR=\frac{dR}{G} \end{equation} ($L_{Pl}^2=\hbar G/c^3$). The quantity $dR$ can be presented in the form \begin{equation} \label{HolPr:15_2} dR=-H\dot{H}R^3dt. \end{equation} On other hand, the energy flow through the Hubble sphere can be calculated if one is given the energy-momentum tensor for the substance filling the Universe. Treating the latter as an ideal fluid (see Chapter 2) and using the relation $T_{\mu \nu }=(\rho +p)u_{\mu }u_{\nu }+pg_{\mu \nu },$ one obtains \begin{equation} \label{HolPr:15_3} dE=A\left( \rho +p \right)dt \end{equation} Equating (\ref{HolPr:15_1}) and (\ref{HolPr:15_3}) and taking into account (\ref{HolPr:15_2}), one finds \begin{equation} \label{HolPr:15_4} \dot{H}=-4\pi G\left( \rho +p \right). \end{equation} As it was shown in Chapter 2, the system of equations \begin{align} \nonumber & \dot{H}=-4\pi G\left( \rho +p \right);\\ & \dot{\rho }+3H\left( \rho +p \right)=0, \end{align} is equivalent to the standard system of Friedman equations \begin{align} \nonumber H^2 = & \frac{8\pi G}{3}\rho ; \\ \frac{\ddot{a}}{a} = & -\frac{4\pi G}{3}(\rho +3p). \end{align} The application of this method to obtain the Friedman equations for a non-flat Universe will be considered in the next problem. 2nd method. Consider a compact spatial region $V$ with boundary $\partial V,$ which represents a sphere with physical radius $R=ar.$ The boundary acts as a holographic screen. Assume that the number of bits on the screen equals to $$ N=\frac{Ac^3}{G\hbar }, $$ and the equipartition theorem gives $$ E=Mc^2=\frac{1}{2}Nk_{_B}T. $$ In this relation the mass $M$ is equal to the total mass in the region enclosed by the spherical holographic screen. As usual, assume that the matter filling the considered region is ideal fluid with the energy-momentum tensor $$ T_{\mu \nu }=\left( p+\rho \right)u_{\mu }u_{\nu }+pg_{\mu \nu }. $$ Total mass in the spatial region $V$ is $$ M=\int_{V}{dV}\left(T_{\mu \nu }u^{\mu }u^{\nu }\right). $$ Here $T_{\mu \nu }u^{\mu }u^{\nu }$ is the energy density measured by the comoving observer with $4$-velocity $u^\mu$. On the other hand, acceleration for radial comoving observer in the point $r,$ i.e. in the point where the screen is situated, equals to $$ a_r=\frac{d^2R}{dt^2}=-\ddot{a}r $$ The minus sign appears because one considers the acceleration caused by matter in the region enclosed by the screen. According to the Unruh formula (\ref{Hol_f_Unruh:4}), this acceleration corresponds to temperature $$ T=\frac{1}{2\pi k_{_B}c}\hbar a_{r}. $$ Substitution of the quantities determined above into the equipartition theorem gives $$ \ddot{a}=-\frac{4\pi G}{3}\rho a. $$ This is nothing else then the Newton analogue of the second Friedman equation. In order to obtain the exact Friedman equation, which follows from General Relativity, one has to use the so-called active gravitational mass $$ M^*=2\int_{V}dV\left(T_{\mu \nu }-\frac{1}{2}Tg_{\mu \nu }\right)u^{\mu }u^{\nu }. $$ Replacing $M$ by $M^*$, one obtains $$ \frac{\ddot{a}}{a}=-\frac{4\pi G}{3}\left( \rho +3p \right) $$ Multiplying both sides of the latter equality by $\dot{a}a$ and using the conservation equation $$ \dot{\rho }+3H\left( \rho +p \right)=0, $$ one obtains the first Friedman equation $$ H^2+\frac{k}{a^2}=\frac{8\pi G}{3}\rho. $$ Here $k$ is the integration constant, which can be treated as the spatial curvature in the region $V.$
Problem 1:
Derive the Friedman equations from the holographic principle for a non-flat Universe.
Repeat all the steps similar to (\ref{HolPr:15_1}) - (\ref{HolPr:15_4}), using for $R_H$ the expression obtained in problem \ref{equ24n} of Chapter 2 \begin{equation} \label{R_H} R_H=\frac{1}{\sqrt{H^2+\frac{k}{a^2}}}, \end{equation} to obtain \begin{equation} \dot{H}=-4\pi G(\rho +p)+\frac{k}{a^2}. \end{equation} Combined with the conservation equation, it is equivalent to \begin{align} \nonumber & H^2=\frac{8\pi G}{3}\rho -\frac{k}{a^2}; \label{Fridmann_eq}\\ & \frac{\ddot{a}}{a}=-\frac{4\pi G}{3}(\rho +3p). \\ \nonumber \end{align}
Problem 1:
Consider an effective field theory with the ultraviolet cutoff parameter equal to $\Lambda$ and entropy satisfying the inequality \[S\equiv L^3\Lambda^3\le S_{BH}\simeq L^2 M_{Pl}^2,\] where $S_{BH}$ is the Beckenstein-Hawking entropy, and show that such a theory necessarily contains the states with Schwarzschild radius $R_S$ much greater than the linear dimensions $L$ of the system. (see Zimdahl, Pavon, 0606555)
For sufficiently high temperatures ($T\gg {{L}^{-1}}$, but $T\le \Lambda $) the energy of the system is $E$ $\simeq {{L}^{3}}{{T}^{4}}$, and its entropy $S\simeq {{L}^{3}}{{T}^{3}}$. When the inequality \[S\le {{S}_{BH}}\] is saturated (let us assume that $T=\Lambda $), then $T\simeq {{\left( M_{Pl}^{2}/L \right)}^{1/3}}$. On the other hand, the Schwarzschild radius is related to the energy as ${{R}_{s}}\simeq E/M_{Pl}^{2}$ . Therefore ${{R}_{S}}\gg L$.
Problem 1:
Estimate the dark energy density assuming that the total energy in a region with linear size $L$ cannot exceed the black hole mass of the same size.
$$ \rho_{_{DE}} \le \frac{c}{2GL^2}. $$ Saturation of the inequality is equivalent to the choice of maximum allowed value for $L.$ In cosmological context it is reasonable to chose $L$ equal to the current size of the Universe, i.e. Hubble scale $L\sim H^{-1}$ (the quantities similar to $L$ in holographic physics are called the infrared cutoff scale (IR cutoff)). Then according to the holographic principle $\rho_{_{DE}}\propto H^{2}$ For $\hbar =c=1$ the restriction formulated in the statement of the problem can be presented in the form $$ L^3\rho_{DE}\le LM_{Pl}^{2} $$ Saturation of this inequality is equivalent to the choice of maximum allowed value for $L.$ In cosmological context it is reasonable to chose $L$ equal to current size of Universe, i.e. Hubble scale $L\sim H^{-1}.$ Then $$ \rho_{DE}\sim H^2M_{Pl}^{2} $$ and \begin{align} \nonumber M_{Pl} & \simeq 1.2\times 10^{19} \;\mbox{\it GeV };\\ \nonumber {{H}_{0}} & \simeq 1.6\times {{10}^{-42}}\;\mbox{\it GeV } \\ \nonumber \rho_{_{DE}} & \sim 10^{-46}\;\mbox{\it GeV}^{4}. \end{align} This value differs only by two orders of magnitude from the observed density of dark energy $\rho _{DE}^{\left( obs \right)}\sim 10^{-48}\;\mbox{\it GeV}^{4}$. Recall that dimensional estimate in the frame of SCM led to divergence of 120(!) orders of magnitude.
Problem 1:
Find the correspondence between the ultraviolet and infrared cutoff scales.
Holographic principle applied to black holes as objects with maximum entropy in a given region of space states that the maximum entropy inside the region is proportional only to the surface area of the region, and the number of independent degrees of freedom is limited by the value of the surface area expressed in Planck units (\ref{Hol_f:1}): $$ N\leq \frac{Ac^3}{G\hbar}. $$ Therefore effective quantum field theory with ultraviolet cutoff $\Lambda $ defined in the region of linear size $L,$ with entropy proportional to $S\sim L^3\Lambda^3,$ must satisfy the condition \begin{equation} \label{conditionQFT} L^3\Lambda^3\le S_{BH}\equiv \frac{1}{4}\frac{A}{l_{Pl}^2}=\pi L^2M_{PL}^2 \end{equation} where $S_{BH}$ is entropy of black hole of radius $L.$ Thus the latter relation shows that the value of the infrared cutoff (IR cutoff) cannot be chosen independently from the ultraviolet cutoff value: \begin{equation} \label{LsimLambda{-3}} L\sim \Lambda^{-3} \end{equation} In other words in quantum field theory the ultraviolet cutoff on small scales is related to the infrared cutoff on large scales (See one of the early works on the topic: Andrew G. Cohena, David B. Kaplanb and Ann E. Nelsonc, Effective Field Theory, Black Holes, and the Cosmological Constant, arXiv:hep-th/9803132v2 31 Mar 1999).
Problem 1:
Show that the entropy force produces negative pressure.
Problem 1:
Taking the Hubble sphere for the holographic screen, and using the SCM parameters, find the entropy, the force acting on the screen and the corresponding pressure.
Entropy contained on the Hubble sphere is \begin{equation} S_H = \frac{k_B c^3}{G \hbar} \frac{A}{4} = \frac{k_B c^3} {G \hbar} \pi R_H^2 = \frac{k_B c^3} {G \hbar} \pi \left( \frac{c}{H} \right)^2 \sim (2.6 \pm 0.3) \times 10^{122} k_B \end{equation} Note that change of Hubble radius $R_H$ by $\Delta r$ causes the entropy change equal to \begin{equation} \Delta S_H = \frac{k_B c^3} {G \hbar} 2\pi R_H \Delta r = \frac{k_B c^3} {G \hbar} 2\pi \left( \frac{c}{H} \right) \Delta r \sim (2.6 \pm 0.3) \times 10^{122} k_B \Delta r / R_H. \end{equation} The force acting on the holographic screen then is \begin{equation} F_r = - \frac{dE}{dr} = - T \frac{dS}{dr} = - T_\beta \frac{ d S_H}{d r} = - \frac{\hbar}{ k_B }~\frac{ H }{ 2 \pi} \frac{k_B c^3} {G \hbar} 2\pi \left( \frac{c}{H} \right) = - \frac{c^4 }{ G}. \end{equation} The minus sign points on the fact that the force acts in the direction of expanding of the holographic screen. The corresponding pressure takes the form \begin{equation} P = \frac{F_r}{A} = - \frac{1}{A} T \frac{dS}{dr} = - \frac{1}{A} \frac{c^4 }{ G} = - \frac{1}{ 4 \pi c^2/H^2} \frac{c^4 }{ G} = - \frac{c^2 H^2 }{4 \pi G} = - \frac{2}{3} \rho_{cr} c^2, \end{equation} where $\rho_{cr}$ is critical energy density, equal to $\rho_{cr} \equiv 3 H^2 /8 \pi G$.
Problem 1:
The most popular approach to explain the observed accelerated expansion of the Universe assumes introduction of dark energy in the form of cosmological constant into the Friedman equations. As we have seen in the corresponding Chapter, this approach is successfully realized in SCM. Unfortunately, it leaves aside the question of the nature of the dark energy. An alternative approach can be developed in the frame of holographic dynamics. In this case it is possible to explain the observations without the dark energy. It is replaced by the entropy force, acting on the cosmological horizon (Hubble sphere) and leading to the accelerated Universe's expansion.
Show that the Hubble sphere acceleration obtained this way agrees with the result obtained in SCM.
As shown in SCM (see problem \ref{SCM6} of Chapter 11), acceleration of an object situated on distance $R$ from the observer equals to $$ \dot{V}=H_{0}^{2}\left( \Omega_{\Lambda }-\frac{1}{2}\Omega_{m}\right)R. $$ For $R=4000\;\mbox{\it Mpc}$ (size of the observable Universe), $\dot{V}\simeq 4\times {{10}^{-10}}\;\mbox{\it m/sec}^2.$ Using the solution of problem \ref{HU12} of the present Chapter, one can find that acceleration of the Hubble sphere equals to $$ a_{_H}=\frac{2\pi ck_{_B}}{\hbar }T_{U}(a=g)=cH_0\simeq 10^{-9}\;\mbox{\it m/sec}^2. $$ This results agrees by the order of magnitude with the previously obtained estimate in the frame of SCM.
Problem 1:
Plot the dependence of the deceleration parameter on the red shift in the Universe composed of non-relativistic matter. Take into account the negative pressure generated by the entropy force (see Problem \ref{HU26}). Compare the result with the SCM.
The easiest way to take into account the negative pressure generated by the entropic force is to modify the right hand side of the second Friedman equation by addition of a corresponding term. In order to do that one can use dimensional considerations, which results in the following relation \begin{equation} \frac{\ddot a}{a}=-\frac{4\pi G}{3}(\rho+3p)+\frac{a_e}{R_b}. \end{equation} Note that distance to the holographic screen does not have to coincide with the Hubble radius, therefore it is reasonable to choose the holographic screen with the radius \begin{equation} R_b=\frac{1}{\beta H}, \end{equation} and corresponding temperature of the holographic screen takes the form \begin{equation} T_H=\frac{\beta H}{2\pi}. \end{equation} Thus the modified equation becomes \begin{equation} \label{Fridmann_eqIIm} \frac{\ddot a}{a}=-\frac{4\pi G}{3}(\rho+3p)+\beta^2H^2. \end{equation} The deceleration parameter depends on the redshift as $$ q(z) = -1 +\frac{1+z}{H(z)}\frac{dH}{dz} $$ (see the picture).
In The frame of $\Lambda CDM$ the dependence of deceleration parameter on redshift is determined by $$ q = \frac{1}{2}\frac{\Omega _M^{(0)}(1 + z)^3- 2\Omega _\Lambda ^{(0)}} {\Omega _M^{(0)}(1 + z)^3+\Omega_\Lambda ^{(0)}}, $$ where $\Omega _M^{(0)}$ and $\Omega_\Lambda ^{(0)}$ are relative densities of non-relativistic matter and cosmological constant respectively. Recall that in the frame of $\Lambda CDM$ one usually takes $ \Omega _M^{(0)} = 0.27,[[User:Cosmo All|Cosmo All]] \Omega_\Lambda ^{(0)}=0.73. $ The presented plots demonstrate both good qualitative and quantitative agreement between holographic dark energy model ($HCDM$) and $\Lambda CDM$: both models give the same asymptotes and similar behavior near the intersection with the $z$-axis:
$$ q(z \to \infty ) = \frac{1}{2},[[User:Cosmo All|Cosmo All]]\;q(z \to - 1) = - 1. $$
Problem 1:
Show that the coincidence problem does not arise in the models with the holographic dark energy.
As shown above (see problem), the holographic dark energy can be presented in the form $$ \rho_{_{HDE}} = \alpha^2H^2. $$ Consider Universe composed of non-relativistic matter and holographic dark energy \begin{align} H^2= & \frac 13 \left(\rho_{m}+\rho_{_{HDE}}\right);\\ \frac{3-\alpha^2}{\alpha^2}= & \frac{\rho_{m}}{\rho_{_{HDE}}} = const. \end{align} Thus the ratio of both densities remains constant during all evolution of the Universe, which solves the coincidence problem (but produces another problem, see the next problem).
Problem 1:
Show that the holographic screen in the form of Hubble sphere cannot explain the accelerated expansion of Universe.
Consider a Universe dominated by holographic dark energy: $$ \rho_{_{HDE}} = \alpha^2H^2. $$ Use the conservation equation $\dot{\rho}+3H\left( \rho +p\right)=0,~p=w\rho$ \begin{equation} w = -1- \frac{1}{ 3}\frac{d\ln\rho}{d\ln a} = -\frac{1}{3}. \end{equation} Take into account the second Friedman equation $$\frac{\ddot a}{a}=-\frac{4\pi G}{3}(\rho+3p).$$ to obtain the result that $\ddot a = 0.$
Problem 1:
Find the dependence of holographic dark energy density on the scale factor taking the cosmological particle horizon $R_p$ as the holographic screen. Show that such choice cannot explain the accelerated expansion of the Universe.
\begin{align}\nonumber \rho_{_{HDE}} & =3c^2M_p^2L^{-2},\\ \nonumber H^2 & =\frac{1}{3M_p^2}\rho. \end{align} Consider Universe composed of holographic dark energy $$ H^2=c^2L^{-2} $$ and use the definition \begin{equation}\nonumber R_p = a\int^a_0 \frac{da'}{H(a')a'^2}. \end{equation} Then take into account the relation $L=R_p$ to obtain $$ HR_p = c, $$ and therefore $$ \frac{1}{Ha^2}=c\frac{d}{ da}\left(\frac{1}{ Ha}\right). $$ It then follows that $$H^{-1}=\alpha a^{1+\frac{1}{c}}.$$ Thus in the case when the holographic screen coincides with the cosmological particle horizon the holographic dark energy density depends on the scale factor as $$ \rho_{_{HDE}}=3c^2\alpha^{-2} M_p^2 a^{-2(1+\frac{1}{c})}. $$ Use the conservation equation $\dot{\rho}+3H\left( \rho +p\right)=0,~p=w\rho$ to obtain $$ w = -1- \frac{1}{ 3}\frac{d\ln\rho}{d\ln a} = -\frac{1}{ 3}+\frac{2}{ 3c}>-\frac{1}{3} $$ Thus the given cosmological model is unable to provide the accelerated expansion of the Universe.
Problem 1:
Obtain the equation of motion for the relative density of the holographic dark energy in the case when the particle horizon serves as the holographic screen.
The particle horizon is defined as \begin{equation} R_{p}=a(t)\int^{t}_{0}\frac{dt'}{a}=a\int^{a}_{0}\frac{da'}{Ha'^{2}}. \end{equation} After the algebra analogous to that of problem (\ref{HU36}), one obtains \begin{equation} \Omega_{\Lambda}'=\Omega_{\Lambda}\left(1-3\Omega_{\Lambda}-\frac{2}{c}\sqrt{\Omega_{\Lambda}}\right),\label{eq:PHEQ} \end{equation}
Problem 1:
Solve the equation of motion obtained in the previous problem.
Solution of the equation reads \begin{align} \nonumber \frac{1}{\sqrt{1+3c^2}}\big[\ln\left(\sqrt{1+3c^2}+1+3c\sqrt{\Omega_\Lambda}\right) & -\ln\left(1+3c\sqrt{\Omega_\Lambda}-\sqrt{1+3c^2}\right)\big]\\ +\ln\Omega_{\Lambda}-\ln\left(3c\Omega_{\Lambda}+2\sqrt{\Omega_{\Lambda}}-c\right) & =-\ln a+D_0, \\ D_0 =\ln\Omega_{\Lambda0}-\ln\left(3c\Omega_{\Lambda0}+2\sqrt{\Omega_{\Lambda0}}-c\right) & \\ \nonumber +\frac{1}{\sqrt{1+3c^2}}\big[\ln\left(\sqrt{1+3c^2}+1+3c\sqrt{\Omega_{\Lambda0}}\right) & -\ln\left(1+3c\sqrt{\Omega_{\Lambda0}}-\sqrt{1+3c^2}\right)\big], \end{align} where the integration constant $D_0$ is defined by the condition $a_0=1$.
Problem 1:
Find dependence the of holographic dark energy density on the scale factor taking the cosmological event horizon $R_h$ as the holographic screen. Find the equation of state parameter for such a dark energy.
The event horizon limits the current region of the Universe, from which the information can reach us during time $t_{max}$ in the future $$ R_h =a(t)\int^{t_{max}}_t \frac{dt'}{a(t')}. $$ Usually one takes $t_{max}$ equal either to $t=\infty$ or the time when the closed Universe collapses. In the latter case $$ HR_h = c, $$ and therefore $$ H = \alpha a^{-(1-\frac{1}{c})}. $$ Thus in the case when the holographic screen coincides with the cosmological event horizon the holographic dark energy density depends on the scale factor as $$ \rho_{_{HDE}}=3c^2\alpha^{-2} M_p^2 a^{-2(1-\frac{1}{c})}. $$ $$ w = -1- \frac{1}{ 3}\frac{d\ln\rho}{d\ln a} = -\frac{1}{3}-\frac{2}{ 3c}<-\frac{1}{ 3}. $$ The case $c = 1$ corresponds to the cosmological constant with $w=-1.$
Problem 1:
Obtain the equation of motion for the relative density of the holographic dark energy in the case when the event horizon serves as a holographic screen.
The cosmological horizon is \begin{equation} R_{h}=a\int^{\infty}_{t}\frac{dt'}{a}=a\int^{\infty}_{a}\frac{da'}{Ha'^{2}}\label{eq:eh} \end{equation} and the holographic dark energy densities takes the form \begin{equation} \rho_{\Lambda}=3c^2M^2_P/L^2_h.\label{eq:ehvv} \end{equation} Using the definitions of relative energy density $\Omega_{m}=\rho_{m}/(3M^2_PH^2)$ and $\Omega_{\Lambda}=\rho_{\Lambda}/(3M^2_PH^2)$ and the following relation between them \begin{equation} \Omega_{m}+\Omega_{\Lambda}=1, \end{equation} one can obtain the logarithmic derivative of the Hubble parameter with respect to the scale factor's logarithm \begin{equation} \frac{d\ln H}{d\ln a}+\frac{3}{2}\left(1-\Omega_{\Lambda}\right)=0.\label{eq:diffH} \end{equation} Combine (\ref{eq:eh}), (\ref{eq:ehvv}) and the definition of $\Omega_{\Lambda}$ to obtain \begin{equation} \int^{\infty}_{a}\frac{d\ln a'}{Ha'}=\frac{c}{aH}\sqrt{\frac{1}{\Omega_{\Lambda}}}.\label{eq:integral} \end{equation} take derivative by $\ln a$ of both sides of the equation (\ref{eq:integral}) to get \begin{equation} \frac{d\ln H}{dx}+\frac{1}{2}\frac{d\ln\Omega_{\Lambda}}{dx}=\frac{\sqrt{\Omega_{\Lambda}}}{c}-1.\label{eq:Hdx} \end{equation} Substitute (\ref{eq:diffH}) into the equation (\ref{eq:Hdx}) to obtain $\Omega_{\Lambda}$ \begin{equation} \frac{d\Omega_{\Lambda}}{d\ln a}=\Omega_{\Lambda}\left(1-3\Omega_{\Lambda}+\frac{2}{c}\sqrt{\Omega_{\Lambda}}\right),\label{eq:EHEQ} \end{equation}
Problem 1:
Solve the equation of motion obtained in the previous problem.
The equation can be solved exactly \begin{align}\nonumber \frac{1}{\sqrt{1+3c^2}}\big[\ln\left(\sqrt{1+3c^2}+1-3c\sqrt{\Omega_{\Lambda}}\right) - \ln\left(\sqrt{1+3c^2}-1+3c\sqrt{\Omega_{\Lambda}}\right)\big] & \\ +\ln\Omega_{\Lambda} - \ln\left(2\sqrt{\Omega_{\Lambda}}+c-3c\Omega_{\Lambda}\right) & =\ln a+C_0, \end{align} \begin{align}\nonumber C_0 & = \ln\Omega_{\Lambda0} -\ln\left(2\sqrt{\Omega_{\Lambda0}}+c-3c\Omega_{\Lambda0}\right)\\ \nonumber & +\frac{1}{\sqrt{1+3c^2}}\big[\ln\left(\sqrt{1+3c^2}+1-3c\sqrt{\Omega_{\Lambda0}}\right) -\ln\left(\sqrt{1+3c^2}-1+3c\sqrt{\Omega_{\Lambda0}}\right)\big] \end{align} where the integration constant $C_0$ can be determined from the condition $a_0=1$.
Problem 1:
Find the dependence of cosmological parameters (Hubble parameter $H$, state equation parameter $w$ and deceleration parameter $q$) on red shift in the model of the Universe composed of radiation, non-relativistic matter and holographic dark energy, taking as the holographic screen the Ricci scalar's $R$ characteristic length $$ \rho_{_{RDE}}=-\frac{\alpha}{16\pi} R =\frac{3\alpha}{8\pi}\left(\dot{H}+2H^2+\frac{ k}{a^2}\right), $$ where $\alpha $ is a positive constant, $k $ is the sign of space curvature.
By definition
$$
\rho_{_{RDE}}=-\frac{\alpha}{16\pi} R =\frac{3\alpha}{8\pi}\left(\dot{H}+2H^2+\frac{
k}{a^2}\right).
$$
Introducing the notation $x=\ln (1+z)$, one can transform the first Friedman equation to
\begin{eqnarray}
H^2&=&\frac{8\pi}{3}\left[{{\left(\alpha
-1\right)\frac{3k}{8\pi}}}{e^{2x}}+{\rho_{m}}{e^{3x}}+{\rho_{r}}{{e^{4x}}}\right]\nonumber\\
&&+\alpha\left(2H^2 - \frac{1}{2}\frac{dH^2}{dx}\right),
\end{eqnarray}
where $\rho_m$ and $\rho_{r}$ are densities of non-relativistic and relativistic matter respectively. The deceleration parameter is obtained in the same way.
Evolution of the deceleration parameter is described by
\[q=-\frac{{\ddot{a}}}{a{{H}^{2}}}=\frac{\frac{4\pi G}{3}\left( {{\rho }_{tot}}+3{{p}_{tot}} \right)}{\frac{8\pi G}{3}{{\rho }_{tot}}}=\frac{1}{2}+\frac{3}{2}\frac{{{p}_{tot}}}{{{\rho }_{tot}}}\]
Use the dependencies of density and pressure on scale factor (redshift), obtained in previous problems, to obtain the results presented on Fig.\ref{fig:HolPr24_3-4}.
Acceleration of Universe's expansion starts at $z\simeq 0.55.$ (Compare with the combined analysis of $SNe+CMB$ data with the $\Lambda CDM$, resulting in $z=0.52\div 0.73$)
State equation parameter $w(z)$ and deceleration parameter $q(z)$ for the case of Universe composed of holographic dark energy with Ricci scalar curvature.
Problem 1:
Problem 1:
Problem 1:
Problem 1:
Problem 1:
Problem 1:
Problem 1:
Problem 1:
Problem 1:
Problem 1:
Problem 1:
Problem 1:
Problem 1:
Problem 1:
Problem 1: