Difference between revisions of "Solutions of Friedman equations in the Big Bang model"
(→Problem 35.) |
|||
| Line 16: | Line 16: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">a) Radiation: $p=\frac{1}{3}\rho$, and from energy conservation |
| + | \[\dot{\rho}+4\frac{\dot{a}}{a}\rho=0, | ||
| + | \quad\Rightarrow\quad \rho\sim \frac{1}{a^{4}}.\] | ||
| + | On substitution of this into the first Friedman equation we obtain the equation for $a(t)$ (we use normalization $a_{0}=1$) | ||
| + | \[\frac{\dot{a}^{2}}{a^{2}} | ||
| + | =\frac{8\pi G}{3}\cdot\frac{\rho_{r0}}{a^4}.\] | ||
| + | After integration | ||
| + | \[a(t) = \sqrt[4]{\tfrac{32}{3} | ||
| + | \pi G{\rho _{r0}}}\;t^{1/2} | ||
| + | \quad\mbox{and}\quad | ||
| + | \rho_r (t) | ||
| + | = \frac{1}{\frac{{32}}{3}\pi G{t^2}}.\] | ||
| + | The main result is: | ||
| + | \begin{equation}\label{dyn-radiation} | ||
| + | \rho_{r}\sim \frac{1}{a^{4}}, | ||
| + | \quad a(t) \sim t^{1/2}, | ||
| + | \quad \rho_{r}(t)\sim t^{-2}. | ||
| + | \end{equation} | ||
| + | |||
| + | b) For non-relativistic matter $p=0$, so the energy conservation equation is | ||
| + | \[\dot{\rho}+3\frac{\dot{a}}{a}\rho=0, | ||
| + | \quad\Rightarrow\quad \rho\sim \frac{1}{a^{3}}.\] | ||
| + | In the same way as for the case of radiation domination we get | ||
| + | \[a(t) = \sqrt[3]{{6\pi G{\rho _{m0}}}}\;t^{\frac{2}{3}} | ||
| + | \quad\mbox{and}\quad | ||
| + | \rho_m (t) = \frac{1} {{6\pi Gt^2 }}.\] | ||
| + | Then | ||
| + | \begin{equation}\label{dyn-matter} | ||
| + | \rho_{m}\sim\frac{1}{a^3}, | ||
| + | \quad a(t) \sim t^{\frac{2}{3}}, | ||
| + | \quad \rho_m (t) \sim t^{-2 }. | ||
| + | \end{equation} | ||
| + | Note that the dependence $\rho(t)$ is the same in both cases.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
<div id="dyn6"></div> | <div id="dyn6"></div> | ||
| − | |||
=== Problem 2. === | === Problem 2. === | ||
Consider two spatially flat Universes. One is filled with radiation, the other with dust. The current energy density is the same. Compare energy densities when both of them are twice as old. | Consider two spatially flat Universes. One is filled with radiation, the other with dust. The current energy density is the same. Compare energy densities when both of them are twice as old. | ||
| Line 27: | Line 58: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">The temporal dependence of energy density in a Universe filled with only one component with equation of state $p=w\rho$ (where $w=const$) can be written as |
| + | \[\rho(t)=\rho_{0}\frac{t_0^2}{t^2},\] | ||
| + | where $\rho_0$ is the current density and | ||
| + | \[t_0=\frac{1}{(w+1)\sqrt{6\pi G\rho_0}}\] | ||
| + | is the current age of the Universe. When both Universes are twice older, density will be four times smaller in each of them.</p> | ||
</div> | </div> | ||
</div> | </div> | ||
| Line 37: | Line 72: | ||
<div class="NavHead">solution</div> | <div class="NavHead">solution</div> | ||
<div style="width:100%;" class="NavContent"> | <div style="width:100%;" class="NavContent"> | ||
| − | <p style="text-align: left;"></p> | + | <p style="text-align: left;">If matter and radiation do not interact, as is assumed, we can write down energy conservation laws for them separately. Then for radiation $\rho_{r}\sim a^{-4}$ and for matter $\rho_{m}\sim a^{-3}$, so energy density of radiation in an expanding Universe always decreases faster than that of non-relativistic matter. Thus the dynamics of the Universe can be divided into two stages: the first one when the dominating component is radiation, and the second one when the dominating component is non-relativistic matter. |
| + | |||
| + | The first stage: radiation domination. The first Friedman equation is | ||
| + | \[\left(\frac{\dot a}{a}\right)^2 | ||
| + | = \frac{8\pi G}{3}(\rho_r + \rho_m)\] | ||
| + | When $\rho_r \gg \rho_m$, it takes the form | ||
| + | \[\left( \frac{\dot a}{a} \right)^2 | ||
| + | \approx\frac{8\pi G}{3}\rho_r.\] | ||
| + | Then (see problem \ref{r_m}) $a(t)\sim t^{1/2}$ and $\rho_r \sim t^{-2}.$ | ||
| + | |||
| + | The dominating component determines the behavior of scale factor as function of time. Therefore we have to plug $a(t)$ for the Universe with dominating radiation into $\rho_m = \rho_m(a)$. Then $\rho_m \sim a^{-3} \sim t^{3/2}$. The relative density of matter increases with time, so the stage of radiation domination is succeeded by the stage of matter domination. | ||
| + | |||
| + | Stage 2: matter domination. Following the same train of thought we get | ||
| + | \[ a \sim t^{2/3};\quad\rho _m \sim \frac{1}{t^2}; | ||
| + | \quad\rho _r \sim \frac{1}{a^4} | ||
| + | \sim \frac{1}{t^{8/3}}.\] | ||
| + | |||
| + | [[File:3_11.jpg|frame|Asymptotic behavior of $\rho(t)$ for the case of background interaction of matter and radiation. To [[dyn11|problem ]]]]</p> | ||
</div> | </div> | ||
</div> | </div> | ||
Revision as of 19:08, 9 July 2012
Contents
- 1 Problem 1.
- 2 Problem 2.
- 3 Problem 3.
- 4 Problem 4.
- 5 Problem 5.
- 6 Problem 6.
- 7 Problem 7.
- 8 Problem 8.
- 9 Problem 9.
- 10 Problem 10.
- 11 Problem 11.
- 12 Problem 12.
- 13 Problem 13.
- 14 Problem 14.
- 15 Problem 15.
- 16 Problem 16.
- 17 Problem 17.
- 18 Problem 18.
- 19 Problem 19.
- 20 Problem 20.
- 21 Problem 21.
- 22 Problem 22.
- 23 Problem 23.
- 24 Problem 24.
- 25 Problem 25.
- 26 Problem 26.
- 27 Problem 27.
- 28 Problem 28.
- 29 Problem 29.
- 30 Problem 30.
- 31 Problem 31.
- 32 Problem 32.
- 33 Problem 33.
- 34 Problem 34.
- 35 Problem 35.
- 36 Problem 36.
- 37 Problem 37.
- 38 Problem 38.
Problem 1.
Derive $\rho(a)$, $\rho(t)$ and $ a(t)$ for a spatially flat$^*$ ($k=0$) Universe that consists of only
a) radiation,
b) non-relativistic matter$^{**}$.
$^*$ The "spatial" part is often omitted when there cannot be any confusion (and even when there can be), generally and hereatfer.
$^{**}$ In this context and below also quite often called just "matter" or dust.
a) Radiation: $p=\frac{1}{3}\rho$, and from energy conservation \[\dot{\rho}+4\frac{\dot{a}}{a}\rho=0, \quad\Rightarrow\quad \rho\sim \frac{1}{a^{4}}.\] On substitution of this into the first Friedman equation we obtain the equation for $a(t)$ (we use normalization $a_{0}=1$) \[\frac{\dot{a}^{2}}{a^{2}} =\frac{8\pi G}{3}\cdot\frac{\rho_{r0}}{a^4}.\] After integration \[a(t) = \sqrt[4]{\tfrac{32}{3} \pi G{\rho _{r0}}}\;t^{1/2} \quad\mbox{and}\quad \rho_r (t) = \frac{1}{\frac[[:Template:32]]{3}\pi G{t^2}}.\] The main result is: \begin{equation}\label{dyn-radiation} \rho_{r}\sim \frac{1}{a^{4}}, \quad a(t) \sim t^{1/2}, \quad \rho_{r}(t)\sim t^{-2}. \end{equation} b) For non-relativistic matter $p=0$, so the energy conservation equation is \[\dot{\rho}+3\frac{\dot{a}}{a}\rho=0, \quad\Rightarrow\quad \rho\sim \frac{1}{a^{3}}.\] In the same way as for the case of radiation domination we get \[a(t) = \sqrt[3]{{6\pi G{\rho _{m0}}}}\;t^{\frac{2}{3}} \quad\mbox{and}\quad \rho_m (t) = \frac{1} [[:Template:6\pi Gt^2]].\] Then \begin{equation}\label{dyn-matter} \rho_{m}\sim\frac{1}{a^3}, \quad a(t) \sim t^{\frac{2}{3}}, \quad \rho_m (t) \sim t^{-2 }. \end{equation} Note that the dependence $\rho(t)$ is the same in both cases.
Problem 2.
Consider two spatially flat Universes. One is filled with radiation, the other with dust. The current energy density is the same. Compare energy densities when both of them are twice as old.
The temporal dependence of energy density in a Universe filled with only one component with equation of state $p=w\rho$ (where $w=const$) can be written as \[\rho(t)=\rho_{0}\frac{t_0^2}{t^2},\] where $\rho_0$ is the current density and \[t_0=\frac{1}{(w+1)\sqrt{6\pi G\rho_0}}\] is the current age of the Universe. When both Universes are twice older, density will be four times smaller in each of them.
Problem 3.
Find the scale factor and density of each component as functions of time in a flat Universe which consists of dust and radiation, for the case one of the components is dominating. Present the results graphically.
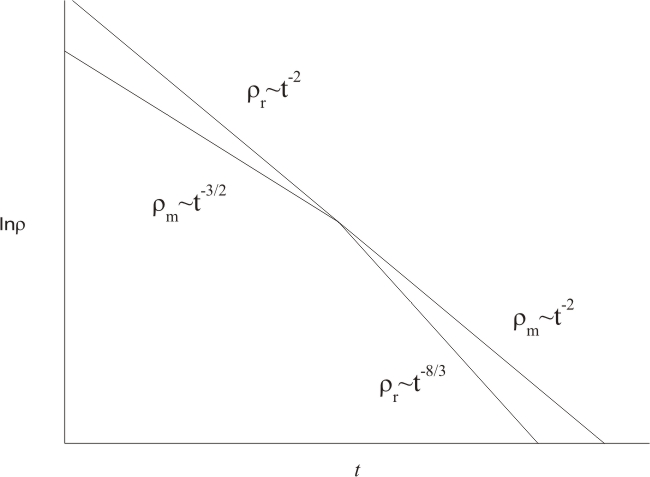
If matter and radiation do not interact, as is assumed, we can write down energy conservation laws for them separately. Then for radiation $\rho_{r}\sim a^{-4}$ and for matter $\rho_{m}\sim a^{-3}$, so energy density of radiation in an expanding Universe always decreases faster than that of non-relativistic matter. Thus the dynamics of the Universe can be divided into two stages: the first one when the dominating component is radiation, and the second one when the dominating component is non-relativistic matter. The first stage: radiation domination. The first Friedman equation is \[\left(\frac{\dot a}{a}\right)^2 = \frac{8\pi G}{3}(\rho_r + \rho_m)\] When $\rho_r \gg \rho_m$, it takes the form \[\left( \frac{\dot a}{a} \right)^2 \approx\frac{8\pi G}{3}\rho_r.\] Then (see problem \ref{r_m}) $a(t)\sim t^{1/2}$ and $\rho_r \sim t^{-2}.$ The dominating component determines the behavior of scale factor as function of time. Therefore we have to plug $a(t)$ for the Universe with dominating radiation into $\rho_m = \rho_m(a)$. Then $\rho_m \sim a^{-3} \sim t^{3/2}$. The relative density of matter increases with time, so the stage of radiation domination is succeeded by the stage of matter domination. Stage 2: matter domination. Following the same train of thought we get \[ a \sim t^{2/3};\quad\rho _m \sim \frac{1}{t^2}; \quad\rho _r \sim \frac{1}{a^4} \sim \frac{1}{t^{8/3}}.\]
Problem 4.
Derive the time dependence of the Hubble parameter for a flat Universe in which either matter or radiation is dominating.
Problem 5.
Derive the exact solutions of the Friedman equations for the Universe filled with matter and radiation. Plot the graphs of scale factor and both densities as functions of time.
Problem 6.
At what moment after the Big Bang did matter's density exceed that of radiation for the first time?
Problem 7.
Determine the age of the Universe in which either matter or radiation has always been dominating.
Problem 8.
Derive the dependence $a(t)$ for a spatially flat Universe that consists of matter with equation of state $p=w\rho$, assuming that the parameter $w$ does not change throughout the evolution.
Problem 9.
Find the Hubble parameter as function of time for the previous problem.
Problem 10.
Using the first Friedman equation, construct the effective potential \label{V(a)} $V(a)$, which governs the one-dimensional motion of a fictitious particle with coordinate $a(t)$, for the Universe filled with several non-interacting components.
Problem 11.
Construct the effective one-dimensional potential $V(a)$ (using the notation of the previous problem) for the Universe consisting of non-relativistic matter and radiation. Show that motion with $\dot{a}>0$ in such a potential can only be decelerating.
Problem 12.
Derive the exact solutions of the Friedman equations for the Universe with arbitrary curvature, filled with radiation and matter.
Problem 13.
Show that for a spatially flat Universe consisting of one component with equation of state $p = w\rho$ the deceleration parameter $q\equiv -\ddot{a}/(aH^2)$ is equal to $\frac{1}{2}(1 + 3w)$.
Problem 14.
Express the age of the Universe through the deceleration parameter $q=-\ddot{a}/(aH^2)$ for a spatially flat Universe filled with single component with equation of state $p=w\rho$.
Problem 15.
Find the generalization of relation $q = \frac{1}{2}(1 + 3w)$ for the non-flat case.
Problem 16.
Show that for a Universe consisting of several components with equations of state $p_{i} = w_{i} \rho_{i}$ the deceleration parameter is \[q = \frac{\Omega }{2} + \frac{3}{2}\sum\limits_i {w_i \Omega_i },\] where $\Omega$ is the total relative density.
Problem 17.
For which values of state parameter $w$ the rate of expansion of a one-component flat Universe increases with time?
Problem 18.
Show that for a spatially closed ($k=1$) Universe that contains only non-relativistic matter the solution of the Friedman equations can be given in the form \[a(\eta)=a_{\star}(1-\cos\eta); \qquad t(\eta)=a_{\star}(\eta -\sin\eta); \qquad a_{\star}=\frac{4\pi G\rho_0}{3}; \quad 0<\eta<2\pi.\]
Problem 19.
Find the relation between the maximum size and the total lifetime of a closed Universe filled with dust.
Problem 20.
Suppose we know the current values of the Hubble constant $H_0$ and the deceleration parameter $q_0$ for a closed Universe filled with dust only. How many times larger will it ever become?
Problem 21.
In a closed Universe filled with non-relativistic matter the current values of the Hubble constant is $H_0$, the deceleration parameter is $q_0$. Find the current age of this Universe.
Problem 22.
Suppose in the same Universe radiation is dominating during a negligibly small fraction of total time of evolution. How many times will a photon travel around the Universe during the time from its "birth" to its "death"?
Problem 23.
In a closed Universe filled with dust the current value of the Hubble constant is $H_0$ and of the deceleration parameter $q_0$.
a) What is the total proper volume of the Universe at present time?
b) What is the total current proper volume of space occupied by matter which we are presently observing?
c) What is the total proper volume of space which we are directly observing?
Problem 24.
Find the solution of Friedman equations for spatially open ($k=-1$) Universe filled with dust in the parametric form $a(\eta)$, $t(\eta)$.
Problem 25.
Suppose the density of some component in a spatially flat Universe depends on scale factor as $\rho(t) \sim a^{-n}(t)$. How much time is needed for the density of this component to change from $\rho_1$ to $\rho_2$?
Problem 26.
Using the expression for $H(t)$, calculate the deceleration parameter for the cases of domination of
a) radiation,
b) matter.
Problem 27.
Consider a Universe consisting of $n$ components, with equations of state $p_{i}=w_{i}\rho_{i}$, and find $w_{tot}$, the parameter of the equation of state $p_{tot}=w_{tot}\rho_{tot}$.
Problem 28.
Derive the equations of motion for relative densities $\Omega_{i}=\rho_{i}/\rho_{cr}$ of the two components comprising a spatially flat two-component Universe, if their equations of state are $p=w_i\rho$, $i=1,2$.
Problem 29.
Suppose a Universe is initially filled with a gas of non-relativistic particles of mass density $\rho_{0}$, pressure $p_{0}$, and $c_p/c_v=\gamma$. Construct the equation of state for such a system.
Problem 30.
Derive the expression for the critical density $\rho_{cr}$ from the condition that Hubble's expansion velocity equals the second cosmic velocity (escape velocity) $v=\sqrt{2gR}$.
Problem 31.
Suppose the Universe is filled with non-relativistic matter and some substance with equation of state $p_X=w\rho_X$. Find the evolution equation for the quantity $r \equiv \frac{\rho_m}{\rho _X}$.
Problem 32.
Express the deceleration parameter through the ratio $r$ for the conditions of the previous problem.
Problem 33.
Let a spatially flat Universe be filled with non-relativistic dust and a substance with equation of state $p_{X}= w\rho_{X}$. Show that in case $\rho_{X}\propto H^2$, the ratio $r =\rho_{m}/\rho_{X}$ does not depend on time.
Problem 34.
Show that for the model of the Universe described in the previous problem the parameter $r$ is related with the deceleration parameter as \[\dot{r}=-2H\frac{\Omega_{curv}}{\Omega_X}q.\]
Problem 35.
Show that in the model of the Universe of problem, in case $k=+1$ and $q>0$ (decelerated expansion) $r$ increases with time, in case $k=+1$ and $q<0$ (accelerated expansion) $r$ decreases with time, and for $k=-1$ vice-versa.
The following three problems on power-law cosmology are inspired by Kumar [1].
Problem 36.
Let us consider a general class of power-law cosmologies described by the scale factor \[a(t) =a_{0}\Big(\frac{t}{t_0}\Big)^\alpha,\] where $t_0$ is the present age of theUniverse and $\alpha$ is a dimensionless positive parameter. Show that:
1) the scale factor in terms of the deceleration parameter may be written as \[a(t) =a_{0}\Big(\frac{t}{t_0}\Big)^{1/1 + q}, \quad\text{i.e.}\quad \alpha=\frac{1}{1+q}.\]
2) the expansion of the Universe is described by Hubble parameter \[H=\frac{1}{(1+q)\;t}\] or in terms of redshift \[H(z)=H_{0}(1+z)^{1+q}.\]
Problem 37.
In the power-law cosmology find the age of the Universe at redshift $z$.
Problem 38.
For the power-law cosmology find the luminosity distance between the observer and the object with redshift $z$.