Difference between revisions of "Static Einstein's Universe"
(Created page with "4") |
|||
| Line 1: | Line 1: | ||
[[Category:Dark Energy|4]] | [[Category:Dark Energy|4]] | ||
| + | |||
| + | |||
| + | __NOTOC__ | ||
| + | |||
| + | |||
| + | <div id="DE24"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
| + | Find the static solution of Friedman equations with cosmological constant and non-relativistic matter (static Einstein's Universe). | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">The static solution ($\dot a =0$, $\ddot a =0$) of Friedman equations with cosmological constant | ||
| + | for the case of Universe filled with matter $\left( {p = 0} \right)$ is found from | ||
| + | \begin{align*} | ||
| + | 0 & = {{8\pi G} \over 3}\rho - {k \over {a^2 }} + {\Lambda \over 3};\\ | ||
| + | 0 & = - {{4\pi G} \over 3}\left( {\rho + 3p} | ||
| + | \right) + {\Lambda \over 3}. | ||
| + | \end{align*} | ||
| + | Then | ||
| + | $$ | ||
| + | \rho = {\Lambda \over {4\pi G}};\quad a=\sqrt{\frac{k}{\Lambda}}. | ||
| + | $$</p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="DE25"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
| + | Show that the static Einstein's Universe must be closed. Find the total volume and mass of this Universe. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">As it follows from the solution obtained in the previous problem, for the case $\rho > 0$ the cosmological constant must be positive and thus $k = + 1$. Such Universe has the geometry of the 3-sphere with radius $R = 1/\sqrt \Lambda $, and its volume and mass are respectively | ||
| + | $$ | ||
| + | V = 2\pi ^2 R^3 = 2\pi ^2 \Lambda ^{ - 3/2} ;\quad M = \rho V = | ||
| + | {\pi \over {2G}}\Lambda ^{ - 1/2}. | ||
| + | $$</p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="DE26"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
| + | Find the parameters of static Einstein's Universe filled with cosmological constant and radiation. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">$$ | ||
| + | \rho_r = {\Lambda \over {8\pi G}};\quad a=\frac32\sqrt{\frac{1}{\Lambda}}. | ||
| + | $$</p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="DE27"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
| + | Find the parameters of static Einstein's Universe under the assumption that both matter and radiation are absent. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">In that case \[\rho_\Lambda=\frac{1}{8\pi GR^2}=0,\] and the Einstein's Universe is reduced to flat Minkowski space-time.</p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="DE28"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
| + | Estimate the radius of static Einstein's Universe if the zero-point energy of electromagnetic field is cut off at the classical electron radius. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">Let us cite [http://arxiv.org/abs/astro-ph/0203330 N.Straumann (2002) (arXiv:astro-ph/0203330)]: | ||
| + | <br/> | ||
| + | "From Pauli's discussions with Enz and Thellung we know that Pauli estimated the influence of the zero-point energy of the electromagnetic field---cut off at the classical electron radius---on the radius of the Universe, and came to the conclusion that it "could not even reach to the moon": | ||
| + | <br/> | ||
| + | When, as a student, I heard about this, I checked Pauli's unpublished remark by doing the following little calculation: | ||
| + | <br/> | ||
| + | In units $\hbar=c=1$ the vacuum energy density of the electromagnetic field is | ||
| + | \[\langle | ||
| + | \rho_{vac}\rangle=\frac{8\pi}{(2\pi)^3}\int\limits_0^{\omega_{max}} | ||
| + | \frac{\omega}{2}\omega^2d\omega=\frac{\omega_{max}^4}{8\pi^2},\] | ||
| + | with | ||
| + | \[\omega_{max}=\frac{2\pi}{\lambda_{min}}=\frac{2\pi m_e}{\alpha},\] | ||
| + | where $m_e$ is the electron mass and $\alpha\simeq1/137$ is the fine structure constant. | ||
| + | <br/> | ||
| + | Using the results of the first problem of this section, one obtains | ||
| + | \[\Lambda=\frac{4\pi\langle \rho_{vac}\rangle}{M_{Pl}^2}\Rightarrow | ||
| + | R=\frac{1}{\sqrt\Lambda}=\frac{\alpha^2M_{Pl}}{(2\pi)^{2/3} | ||
| + | m_e^2}\simeq31.6\mbox{\it km}.\] | ||
| + | This is indeed less than the distance to the moon.* | ||
| + | <br/> | ||
| + | *It would be more consistent to use the curvature radius of the static de Sitter solution; the result is the same, up to the factor $\sqrt3$.</p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="DE29"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
| + | Show that Einstein's Universe is unstable. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">The Friedman equations in the case under consideration read: | ||
| + | $$\ddot a = - {{4\pi G} \over 3}\left( \rho _m - 2\rho _\Lambda | ||
| + | \right)a;$$ | ||
| + | \[\left(\frac{\dot a}{a}\right)^2=\frac{8\pi G}{3}(\rho_m+\rho_\Lambda)-\frac{1}{a^2}.\] | ||
| + | From the stationarity condition $\dot a = \ddot a = 0$ one obtains the critical points | ||
| + | \[a_0^{-2}=\frac{8\pi G}{3}(\rho_{m0}+\rho_\Lambda);\quad \rho_{m0}=2\rho_\Lambda. \] | ||
| + | Substituting \[\rho_m = \rho | ||
| + | _{m0} + \delta \rho _m ;\quad a = a_0 + \delta a\] into the second Friedman equation and keeping only the first-order terms, one obtains | ||
| + | \[\delta \ddot a = | ||
| + | - {{4\pi G} \over 3}\delta \rho _m.\] Taking into account that | ||
| + | \[{{\delta \rho _m } \over {\rho _m }} = - 3{{\delta a} \over a},\] one obtains | ||
| + | \[\delta\rho_m=-3\frac{\delta a}{a}\rho_m=-3(\rho_{m0}+\delta\rho_m)\frac{\delta a}{a_0+\delta a}=-3\frac{\rho_{m0}}{a_0}\delta a,\] and finally the equation | ||
| + | $${\delta \ddot a} - 4\pi G\frac{\rho _{m0}}{a_0} \delta a=0.$$ | ||
| + | The equation's general solution is: | ||
| + | $$ | ||
| + | \delta a = C_1e^{\sqrt{4\pi G\frac{\rho_{m0}}{a_0}}\cdot t}+C_2e^{-\sqrt{4\pi G\frac{\rho_{m0}}{a_0}}\cdot t}. | ||
| + | $$ | ||
| + | Its exponents are imaginary \[\omega=\pm i\sqrt{4\pi G\frac{\rho_{m0}}{a_0}}.\] Therefore the static Universe of Einstein is unstable.</p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="DE30"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
| + | What are the concrete mechanisms that drive the instability of the static Einstein's Universe? | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">The static Einstein's Universe will follow unlimited compression in the case when matter starts to transform into radiation; or vice versa, it will unlimitedly expand if radiation transforms into matter. | ||
| + | <br/> | ||
| + | In the latter case the gravity source $\rho + 3p$ decreases, as the pressure of matter equals to zero. Since gravity is a damping force then the equilibrium of static Universe will be shifted towards the expansion. In the case of matter transition into radiation, the gravity source $\rho + 3p$ will increase and the equilibrium will be shifted towards the compression.</p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="DE31"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
| + | What is the most unsatisfactory peculiarity of the static Einstein's model of the Universe (besides the instability)? | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">Absence of redshift for distant objects which is actually observed in the real Universe.</p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="DE32"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
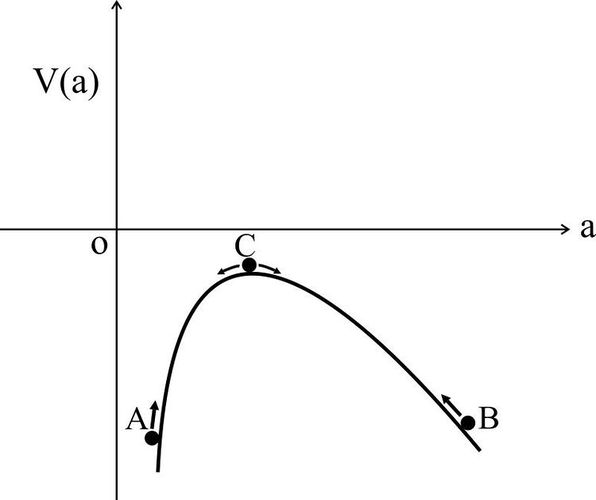
| + | Construct the effective one-dimensional potential $V(a)$ for the case of flat Universe filled with non-relativistic matter and dark energy in the form of cosmological constant. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">$$ | ||
| + | {{\ddot a} \over a} = - {{4\pi G} \over 3}\rho _m + {\Lambda \over | ||
| + | 3};\ \ddot a = - {{\partial V} \over {\partial a}}\Rightarrow\quad V(a) | ||
| + | = - \left( {{{4\pi G} \over 3}\rho _{m0} a^{ - 1} + {{\Lambda a^2 } | ||
| + | \over 6}} \right). | ||
| + | $$ | ||
| + | (See Figure). | ||
| + | <gallery widths=600px heights=500px> | ||
| + | File:Diagram.jpg| | ||
| + | </gallery> | ||
| + | |||
| + | </p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="DE33"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
| + | Show that the static Einstein's Universe may be realized only in the maximum of the effective potential $V(a)$ of the previous problem. | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">The condition of maximum \[{{\partial V(a)} \over {\partial a}} = | ||
| + | 0\] corresponds to the condition of realization of the static Einstein's Universe $\ddot a = 0$.</p> | ||
| + | </div> | ||
| + | </div></div> | ||
| + | |||
| + | |||
| + | |||
| + | <div id="DE34"></div> | ||
| + | <div style="border: 1px solid #AAA; padding:5px;"> | ||
| + | === Problem 1 === | ||
| + | Problem [[#DE32]] can be considered in more general setup.<br/> | ||
| + | Assuming arbitrary values for the contributions of the cosmological constant $\lambda$, matter $\mu$, radiation $\gamma$ and curvature $\varkappa$ respectively, present the first Friedman equation | ||
| + | \begin{equation}\label{Friedman4k+} | ||
| + | H^2\equiv\left(\frac{\dot a}{a}\right)^2=\lambda-\frac{\varkappa}{a^2}+\frac{\mu}{a^3}+\frac{\gamma}{a^4} | ||
| + | \end{equation} | ||
| + | in the form of the energy conservation law \[p^2/2 + U(q) = E.\] | ||
| + | <div class="NavFrame collapsed"> | ||
| + | <div class="NavHead">solution</div> | ||
| + | <div style="width:100%;" class="NavContent"> | ||
| + | <p style="text-align: left;">Equation (\ref{Friedman4k+}) can be presented in Hamiltonian form in the following four ways, depending on what variable is chosen as canonical one: | ||
| + | \begin{eqnarray*} | ||
| + | \begin{array}{c|c|c} | ||
| + | q & U(q) & E\\ | ||
| + | & & \\ | ||
| + | a & -\frac12\left( \lambda q^2 + \frac{\mu}{q} + \frac{\gamma}{q^2}\right) & -\frac\varkappa2\\ | ||
| + | & & \\ | ||
| + | \ln a & -\frac12\left(\mu e^{-3q} + \gamma e^{-4q}-\varkappa e^{-2q} \right) & \frac\lambda2\\ | ||
| + | & & \\ | ||
| + | a^{3/2} & -\frac98\left(\lambda q^2 + \frac{\gamma}{q^{2/3}} - \varkappa q^{2/3} \right) & \frac98\mu\\ | ||
| + | & & \\ | ||
| + | a^2 & -2\left(\lambda q^2 +\mu\sqrt q -\varkappa q\right) & 2\gamma | ||
| + | \end{array} | ||
| + | \end{eqnarray*}</p> | ||
| + | </div> | ||
| + | </div></div> | ||
Revision as of 21:07, 2 December 2012
Problem 1
Find the static solution of Friedman equations with cosmological constant and non-relativistic matter (static Einstein's Universe).
The static solution ($\dot a =0$, $\ddot a =0$) of Friedman equations with cosmological constant for the case of Universe filled with matter $\left( {p = 0} \right)$ is found from \begin{align*} 0 & = {{8\pi G} \over 3}\rho - {k \over {a^2 }} + {\Lambda \over 3};\\ 0 & = - {{4\pi G} \over 3}\left( {\rho + 3p} \right) + {\Lambda \over 3}. \end{align*} Then $$ \rho = {\Lambda \over {4\pi G}};\quad a=\sqrt{\frac{k}{\Lambda}}. $$
Problem 1
Show that the static Einstein's Universe must be closed. Find the total volume and mass of this Universe.
As it follows from the solution obtained in the previous problem, for the case $\rho > 0$ the cosmological constant must be positive and thus $k = + 1$. Such Universe has the geometry of the 3-sphere with radius $R = 1/\sqrt \Lambda $, and its volume and mass are respectively $$ V = 2\pi ^2 R^3 = 2\pi ^2 \Lambda ^{ - 3/2} ;\quad M = \rho V = {\pi \over {2G}}\Lambda ^{ - 1/2}. $$
Problem 1
Find the parameters of static Einstein's Universe filled with cosmological constant and radiation.
$$ \rho_r = {\Lambda \over {8\pi G}};\quad a=\frac32\sqrt{\frac{1}{\Lambda}}. $$
Problem 1
Find the parameters of static Einstein's Universe under the assumption that both matter and radiation are absent.
In that case \[\rho_\Lambda=\frac{1}{8\pi GR^2}=0,\] and the Einstein's Universe is reduced to flat Minkowski space-time.
Problem 1
Estimate the radius of static Einstein's Universe if the zero-point energy of electromagnetic field is cut off at the classical electron radius.
Let us cite N.Straumann (2002) (arXiv:astro-ph/0203330):
"From Pauli's discussions with Enz and Thellung we know that Pauli estimated the influence of the zero-point energy of the electromagnetic field---cut off at the classical electron radius---on the radius of the Universe, and came to the conclusion that it "could not even reach to the moon":
When, as a student, I heard about this, I checked Pauli's unpublished remark by doing the following little calculation:
In units $\hbar=c=1$ the vacuum energy density of the electromagnetic field is
\[\langle
\rho_{vac}\rangle=\frac{8\pi}{(2\pi)^3}\int\limits_0^{\omega_{max}}
\frac{\omega}{2}\omega^2d\omega=\frac{\omega_{max}^4}{8\pi^2},\]
with
\[\omega_{max}=\frac{2\pi}{\lambda_{min}}=\frac{2\pi m_e}{\alpha},\]
where $m_e$ is the electron mass and $\alpha\simeq1/137$ is the fine structure constant.
Using the results of the first problem of this section, one obtains
\[\Lambda=\frac{4\pi\langle \rho_{vac}\rangle}{M_{Pl}^2}\Rightarrow
R=\frac{1}{\sqrt\Lambda}=\frac{\alpha^2M_{Pl}}{(2\pi)^{2/3}
m_e^2}\simeq31.6\mbox{\it km}.\]
This is indeed less than the distance to the moon.*
- It would be more consistent to use the curvature radius of the static de Sitter solution; the result is the same, up to the factor $\sqrt3$.
Problem 1
Show that Einstein's Universe is unstable.
The Friedman equations in the case under consideration read: $$\ddot a = - {{4\pi G} \over 3}\left( \rho _m - 2\rho _\Lambda \right)a;$$ \[\left(\frac{\dot a}{a}\right)^2=\frac{8\pi G}{3}(\rho_m+\rho_\Lambda)-\frac{1}{a^2}.\] From the stationarity condition $\dot a = \ddot a = 0$ one obtains the critical points \[a_0^{-2}=\frac{8\pi G}{3}(\rho_{m0}+\rho_\Lambda);\quad \rho_{m0}=2\rho_\Lambda. \] Substituting \[\rho_m = \rho _{m0} + \delta \rho _m ;\quad a = a_0 + \delta a\] into the second Friedman equation and keeping only the first-order terms, one obtains \[\delta \ddot a = - {{4\pi G} \over 3}\delta \rho _m.\] Taking into account that \[{{\delta \rho _m } \over {\rho _m }} = - 3{{\delta a} \over a},\] one obtains \[\delta\rho_m=-3\frac{\delta a}{a}\rho_m=-3(\rho_{m0}+\delta\rho_m)\frac{\delta a}{a_0+\delta a}=-3\frac{\rho_{m0}}{a_0}\delta a,\] and finally the equation $${\delta \ddot a} - 4\pi G\frac{\rho _{m0}}{a_0} \delta a=0.$$ The equation's general solution is: $$ \delta a = C_1e^{\sqrt{4\pi G\frac{\rho_{m0}}{a_0}}\cdot t}+C_2e^{-\sqrt{4\pi G\frac{\rho_{m0}}{a_0}}\cdot t}. $$ Its exponents are imaginary \[\omega=\pm i\sqrt{4\pi G\frac{\rho_{m0}}{a_0}}.\] Therefore the static Universe of Einstein is unstable.
Problem 1
What are the concrete mechanisms that drive the instability of the static Einstein's Universe?
The static Einstein's Universe will follow unlimited compression in the case when matter starts to transform into radiation; or vice versa, it will unlimitedly expand if radiation transforms into matter.
In the latter case the gravity source $\rho + 3p$ decreases, as the pressure of matter equals to zero. Since gravity is a damping force then the equilibrium of static Universe will be shifted towards the expansion. In the case of matter transition into radiation, the gravity source $\rho + 3p$ will increase and the equilibrium will be shifted towards the compression.
Problem 1
What is the most unsatisfactory peculiarity of the static Einstein's model of the Universe (besides the instability)?
Absence of redshift for distant objects which is actually observed in the real Universe.
Problem 1
Construct the effective one-dimensional potential $V(a)$ for the case of flat Universe filled with non-relativistic matter and dark energy in the form of cosmological constant.
Problem 1
Show that the static Einstein's Universe may be realized only in the maximum of the effective potential $V(a)$ of the previous problem.
The condition of maximum \[{{\partial V(a)} \over {\partial a}} = 0\] corresponds to the condition of realization of the static Einstein's Universe $\ddot a = 0$.
Problem 1
Problem #DE32 can be considered in more general setup.
Assuming arbitrary values for the contributions of the cosmological constant $\lambda$, matter $\mu$, radiation $\gamma$ and curvature $\varkappa$ respectively, present the first Friedman equation
\begin{equation}\label{Friedman4k+}
H^2\equiv\left(\frac{\dot a}{a}\right)^2=\lambda-\frac{\varkappa}{a^2}+\frac{\mu}{a^3}+\frac{\gamma}{a^4}
\end{equation}
in the form of the energy conservation law \[p^2/2 + U(q) = E.\]
Equation (\ref{Friedman4k+}) can be presented in Hamiltonian form in the following four ways, depending on what variable is chosen as canonical one: \begin{eqnarray*} \begin{array}{c|c|c} q & U(q) & E\\ & & \\ a & -\frac12\left( \lambda q^2 + \frac{\mu}{q} + \frac{\gamma}{q^2}\right) & -\frac\varkappa2\\ & & \\ \ln a & -\frac12\left(\mu e^{-3q} + \gamma e^{-4q}-\varkappa e^{-2q} \right) & \frac\lambda2\\ & & \\ a^{3/2} & -\frac98\left(\lambda q^2 + \frac{\gamma}{q^{2/3}} - \varkappa q^{2/3} \right) & \frac98\mu\\ & & \\ a^2 & -2\left(\lambda q^2 +\mu\sqrt q -\varkappa q\right) & 2\gamma \end{array} \end{eqnarray*}